- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Учебно-наглядное, познавательное пособие по математике для младших школьников
Содержание
- 1. Учебно-наглядное, познавательное пособие по математике для младших школьников
- 2. Учебно-наглядное, познавательное пособие по математике для младших школьников
- 3. СодержаниеТанграмАрхимедова играЗадачи на разрезаниеПентаминоТетрамино
- 4. У квадрата большие возможности для создания игрушекДревние
- 5. Геометрический конструкторГеометрические игрушки способствуют формированию и развитию
- 6. Танграм
- 7. ТанграмОдна из самых известных древних геометрических головоломок
- 8. Кто играл в «танграм»?Это настолько увлекательная игра,
- 9. Кто играл в «танграм»?Всем известно, что французский
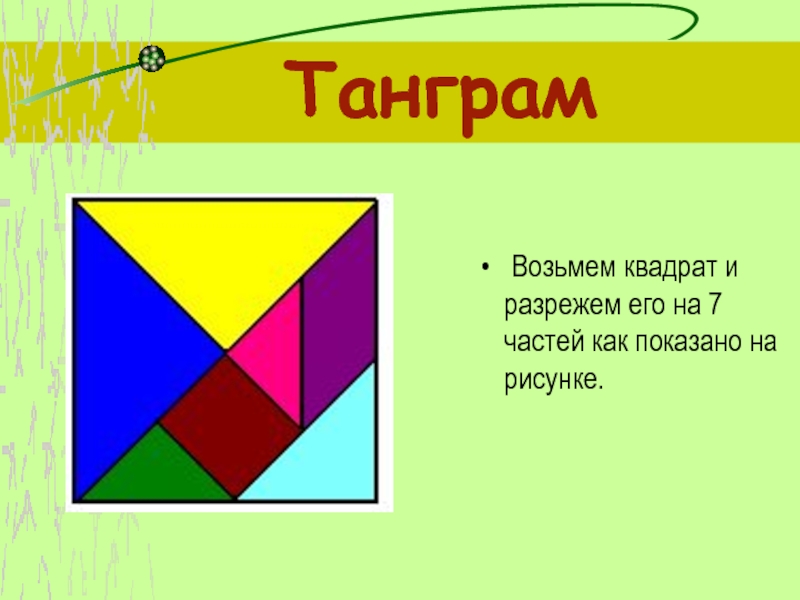
- 10. Танграм Возьмем квадрат и разрежем его на 7 частей как показано на рисунке.
- 11. ТанграмУ нас должно получиться 7 плоских геометрических
- 12. ТанграмБудем называть их так: два больших равных
- 13. Соберем-ка домик
- 14. А,ну-ка,ты собери!
- 15. Фигурки из танов
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Миниатюры из нескольких танов
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Коллекция фигурок-танграмов (225 фигурок по темам имеется у нас для тренировок) Например: Птички
- 33. Архимедова игра Эта игра-головоломка очень похожа на
- 34. Главное отличие от танграма заключается в числе
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Слайд 46
- 47. Задачи на разрезыванияквадратаЕсли вы хоть немного увлечен
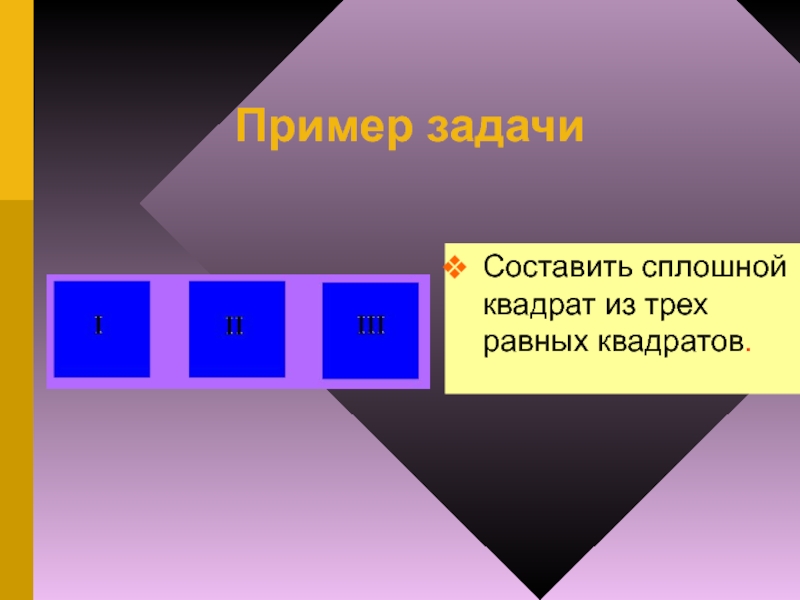
- 48. Пример задачиСоставить сплошной квадрат из трех равных квадратов.
- 49. РешениеПознакомимся с тем решением, которое дал Абул
- 50. Пример задачи на составление квадрата из других
- 51. РешениеНетрудно по рисунку разобраться, как это сделать.
- 52. Пентамино Игра «Пентамино» была придумана в 50-х
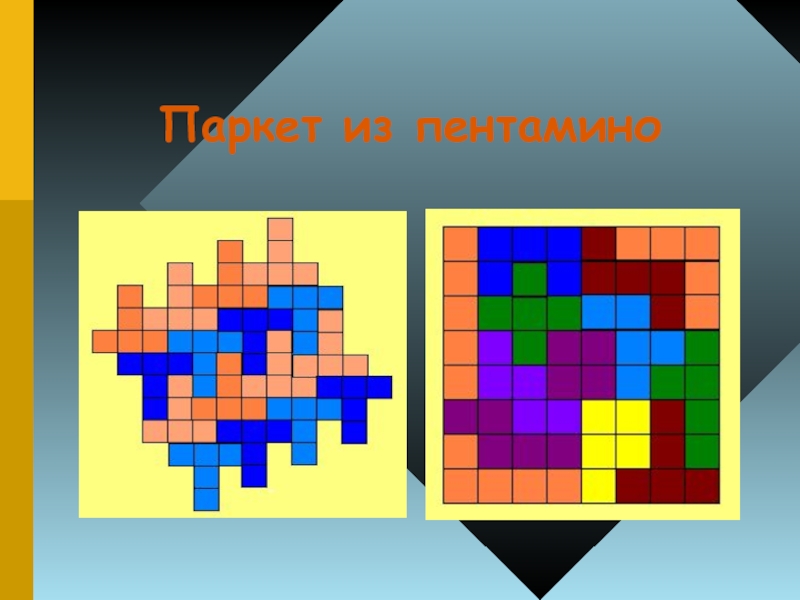
- 53. Паркет из пентамино
- 54. Игра в пентаминоВ пентамино можно играть и
- 55. Тетрамино Тетрамино называется полиомино, занимающее четыре квадрата
- 56. Составление квадратов и прямоугольниковОднако у тетрамино есть
- 57. ЗаключениеИзучая презентацию «Геометрический конструктор», вы, наверное, обратили
Учебно-наглядное, познавательное пособие по математике для младших школьников
Слайд 4У квадрата большие возможности для создания игрушек
Древние греки, китайцы и другие
народы занимались геометрией.
Но они не только измеряли земельные участки и расстояние до кораблей в море, но и любили геометрические игры.
Но они не только измеряли земельные участки и расстояние до кораблей в море, но и любили геометрические игры.
Слайд 5Геометрический конструктор
Геометрические игрушки способствуют формированию и развитию восприятия, пространственного мышления, наблюдательности,
зрительному контролю за выполнением своих действий.
При этом благодаря многим играм развивалась сама математика, появлялись новые разделы высшей математики.
Квадрат очень похож на механизм с хорошо прилаженными частями, который можно разобрать и из тех же частей собрать новый механизм.
При этом благодаря многим играм развивалась сама математика, появлялись новые разделы высшей математики.
Квадрат очень похож на механизм с хорошо прилаженными частями, который можно разобрать и из тех же частей собрать новый механизм.
Слайд 7Танграм
Одна из самых известных древних геометрических головоломок – игра «танграм», в
которую в течение многих веков играют и дети, и взрослые, возникла игра в Китае, где она называется «чи чао ту», то есть умственная головоломка из семи частей. Название «танграм» - европейское. Вероятнее всего, от слова «тань» (что означает «китаец») и корня «грама» (в переводе с греческого «линия»). "Танграм" в переводе - "хитроумный узор из 7 частей".
Слайд 8Кто играл в «танграм»?
Это настолько увлекательная игра, что сам великий древнегреческий
ученый Архимед написал о ней сочинение.
Слайд 9Кто играл в «танграм»?
Всем известно, что французский император Наполеон после военного
поражения был сослан пожизненно на остров Святой Елены. Сведений о том, как он прожил свои последние годы, чем занимался, очень мало.
Но достоверен тот факт, что Наполеон часами занимался складыванием фигур танграма.
Но достоверен тот факт, что Наполеон часами занимался складыванием фигур танграма.
Слайд 11Танграм
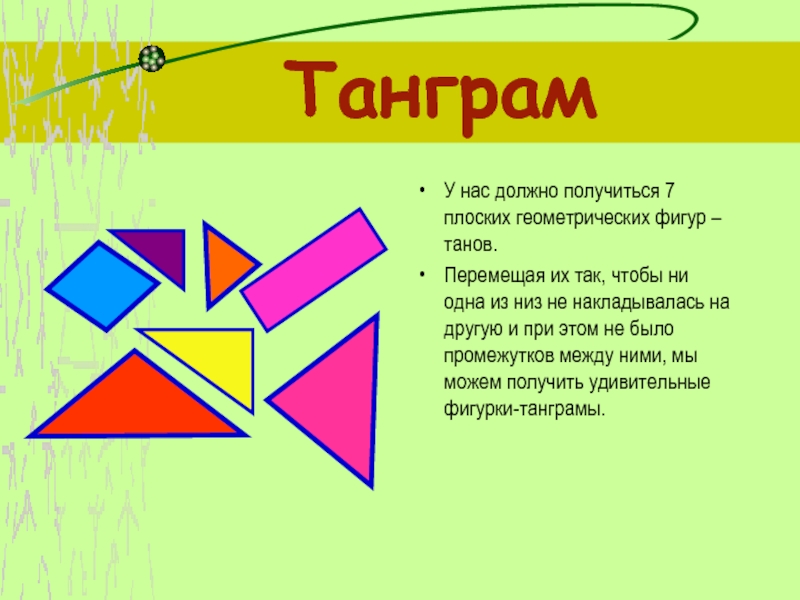
У нас должно получиться 7 плоских геометрических фигур – танов.
Перемещая их
так, чтобы ни одна из низ не накладывалась на другую и при этом не было промежутков между ними, мы можем получить удивительные фигурки-танграмы.
Слайд 12Танграм
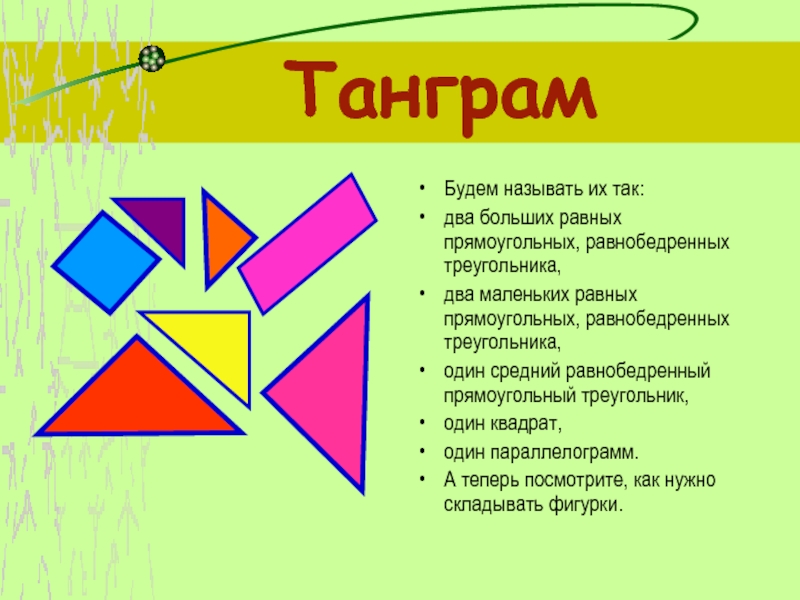
Будем называть их так:
два больших равных прямоугольных, равнобедренных треугольника,
два
маленьких равных прямоугольных, равнобедренных треугольника,
один средний равнобедренный прямоугольный треугольник,
один квадрат,
один параллелограмм.
А теперь посмотрите, как нужно складывать фигурки.
один средний равнобедренный прямоугольный треугольник,
один квадрат,
один параллелограмм.
А теперь посмотрите, как нужно складывать фигурки.
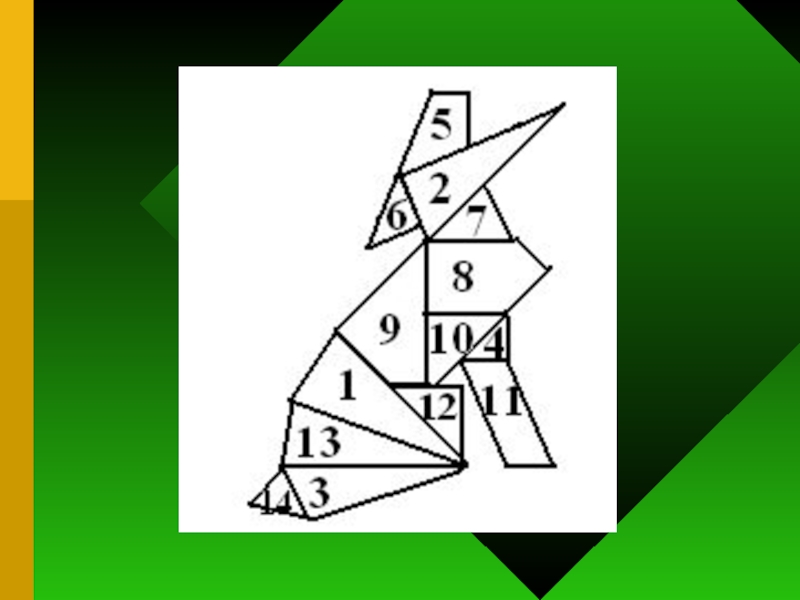
Слайд 32Коллекция фигурок-танграмов
(225 фигурок по темам имеется у нас для тренировок)
Например:
Птички
Слайд 33Архимедова игра
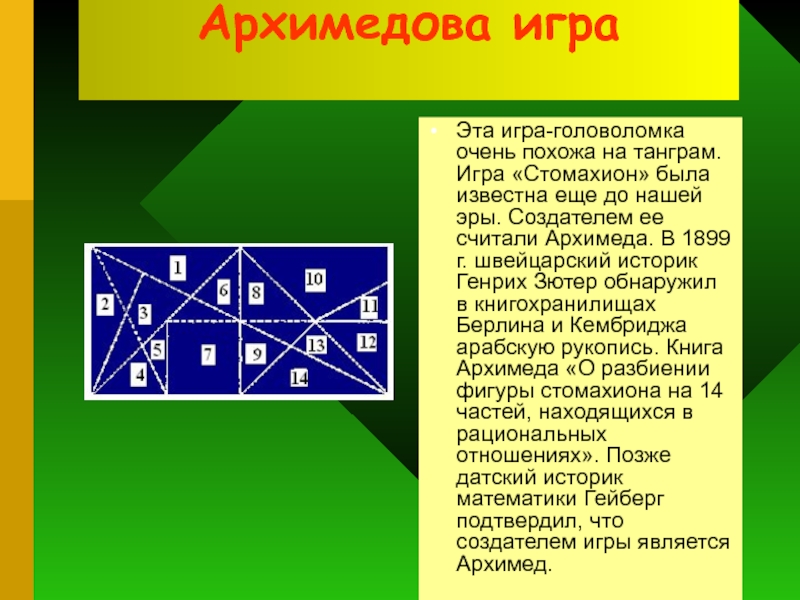
Эта игра-головоломка очень похожа на танграм. Игра «Стомахион» была известна
еще до нашей эры. Создателем ее считали Архимеда. В 1899 г. швейцарский историк Генрих Зютер обнаружил в книгохранилищах Берлина и Кембриджа арабскую рукопись. Книга Архимеда «О разбиении фигуры стомахиона на 14 частей, находящихся в рациональных отношениях». Позже датский историк математики Гейберг подтвердил, что создателем игры является Архимед.
Слайд 34
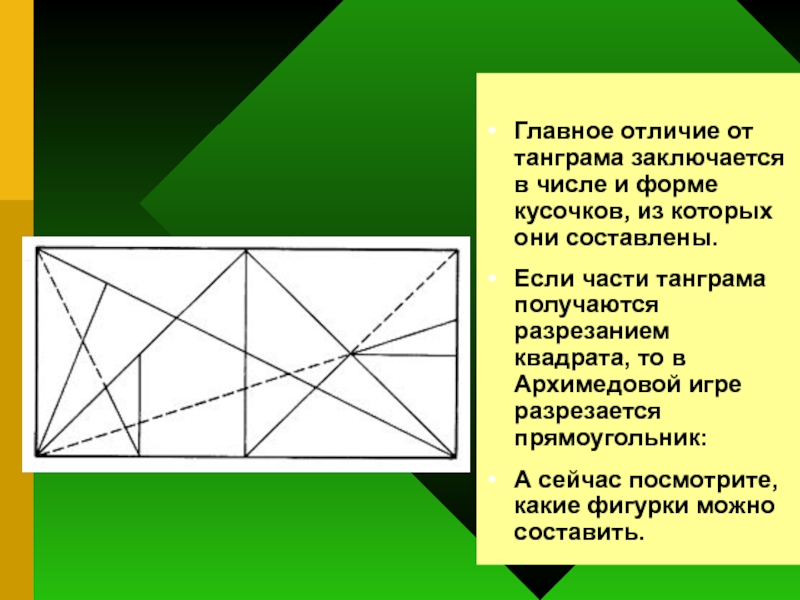
Главное отличие от танграма заключается в числе и форме кусочков, из
которых они составлены.
Если части танграма получаются разрезанием квадрата, то в Архимедовой игре разрезается прямоугольник:
А сейчас посмотрите, какие фигурки можно составить.
Если части танграма получаются разрезанием квадрата, то в Архимедовой игре разрезается прямоугольник:
А сейчас посмотрите, какие фигурки можно составить.
Слайд 47Задачи на разрезыванияквадрата
Если вы хоть немного увлечен математикой, то ему, несомненно,
захочется не только складывать многоугольники из готовых частей квадрата, но и самому научиться разрезать квадрат на части, необходимые для составления той или иной фигуры, например прямоугольного или равностороннего треугольника, правильного пятиугольника или шестиугольника, трех или пяти квадратов и т. д.
На языке геометрии это значит: найти те геометрические построения, при помощи которых разрезается квадрат, и доказать, что из полученных частей может быть составлена требуемая фигура.
Такая постановка вопроса более интересная, но и более трудная.
На языке геометрии это значит: найти те геометрические построения, при помощи которых разрезается квадрат, и доказать, что из полученных частей может быть составлена требуемая фигура.
Такая постановка вопроса более интересная, но и более трудная.
Слайд 49Решение
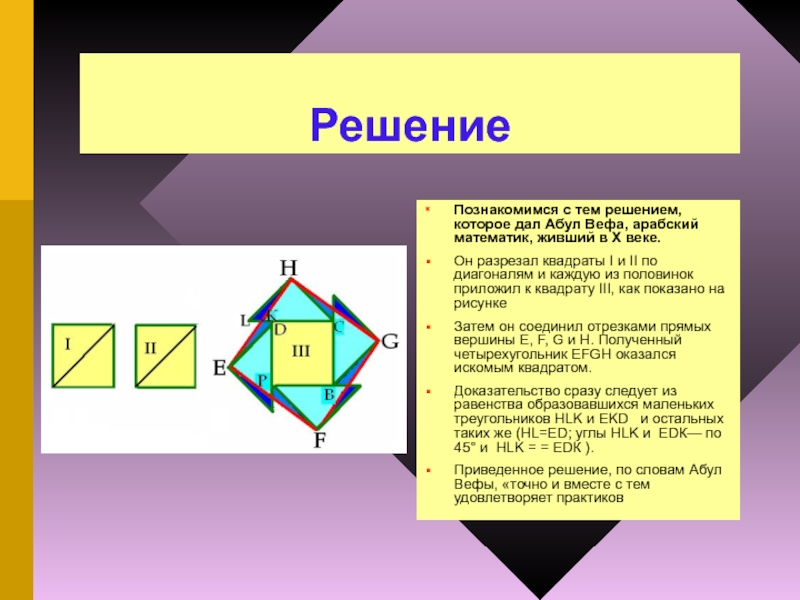
Познакомимся с тем решением, которое дал Абул Вефа, арабский математик, живший
в X веке.
Он разрезал квадраты I и II по диагоналям и каждую из половинок приложил к квадрату III, как показано на рисунке
Затем он соединил отрезками прямых вершины Е, F, G и Н. Полученный четырехугольник ЕFGН оказался искомым квадратом.
Доказательство сразу следует из равенства образовавшихся маленьких треугольников HLK и EKD и остальных таких же (HL=ED; углы HLK и ЕDК— по 45° и HLK = = ЕDК ).
Приведенное решение, по словам Абул Вефы, «точно и вместе с тем удовлетворяет практиков
Он разрезал квадраты I и II по диагоналям и каждую из половинок приложил к квадрату III, как показано на рисунке
Затем он соединил отрезками прямых вершины Е, F, G и Н. Полученный четырехугольник ЕFGН оказался искомым квадратом.
Доказательство сразу следует из равенства образовавшихся маленьких треугольников HLK и EKD и остальных таких же (HL=ED; углы HLK и ЕDК— по 45° и HLK = = ЕDК ).
Приведенное решение, по словам Абул Вефы, «точно и вместе с тем удовлетворяет практиков
Слайд 50Пример задачи на составление квадрата из других фигур
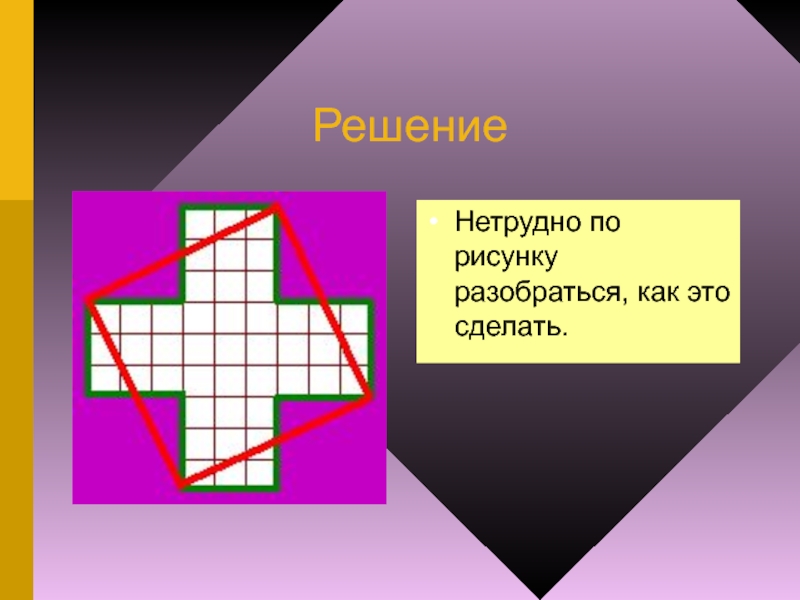
Разрежьте крест на части
и сложите из них квадрат. Причем высота и ширина квадрата должны быть такими же как и высота и ширина креста.
Слайд 52Пентамино
Игра «Пентамино» была придумана в 50-х годах ХХ в. американским математиком
С.Голомбом и очень быстро увлекла не только школьников и студентов, но и профессоров математики.
Она заключается в складывании различных фигур из заданного набора пентамино. Набор пентамино содержит 12 фигурок, каждая из которых составлена из пяти (“пента” по гречески означает «пять») одинаковых квадратов, причем квадраты соседствуют только сторонами.
Она заключается в складывании различных фигур из заданного набора пентамино. Набор пентамино содержит 12 фигурок, каждая из которых составлена из пяти (“пента” по гречески означает «пять») одинаковых квадратов, причем квадраты соседствуют только сторонами.
Слайд 54Игра в пентамино
В пентамино можно играть и вдвоем. двое игроков по
очереди выбирают любую из 12 фигурок пентамино и располагают ее на свободных клетках поля 8 х 8.
Проигрывает тот, кто первым не сможет разместить на доске ни одного пентамино. Если же все фигурки удалось разместить на доске, то выигрывает ходивший последним.
Проигрывает тот, кто первым не сможет разместить на доске ни одного пентамино. Если же все фигурки удалось разместить на доске, то выигрывает ходивший последним.
Слайд 56Составление квадратов и прямоугольников
Однако у тетрамино есть другое интересное свойство. Из
некоторых элементов пентамино (а именно всех, за исключением I, T, X, V) в сочетании с полным набором тетрамино можно составить квадрат 5x5. Вот два таких построения:
Слайд 57Заключение
Изучая презентацию «Геометрический конструктор», вы, наверное, обратили внимание, что роль главной
геометрической фигуры здесь играл квадрат.
Вот такая это интересная, замечательная геометрическая фигура - квадрат, а с виду такая незамысловатая.
Но даже если рассматривать квадрат только для создания игрушек, то таких игрушек будет чрезвычайно много.
Древнегреческие греки, арабы придавали очень большое внимание задачам на разрезывание квадрата, используя выводы в землеустроительстве, в архитектуре.
Квадрату и задачам на разрезывание квадрата посвящено очень много книг.
Вот такая это интересная, замечательная геометрическая фигура - квадрат, а с виду такая незамысловатая.
Но даже если рассматривать квадрат только для создания игрушек, то таких игрушек будет чрезвычайно много.
Древнегреческие греки, арабы придавали очень большое внимание задачам на разрезывание квадрата, используя выводы в землеустроительстве, в архитектуре.
Квадрату и задачам на разрезывание квадрата посвящено очень много книг.