класс МАОУ СОШ №24г. Тамбов
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Центральная и осевая симметрия
Содержание
- 1. Центральная и осевая симметрия
- 2. Выяснить, что же такое симметрия и где
- 3. Осевая симметрия
- 4. Две точки А и А1 называются симметричными
- 5. Являются ли данные точки симметричными ?ММ1mСDbBВ1аРисунок 1Рисунок 2Рисунок 3
- 6. Фигура называется симметричной относительно прямой а, если
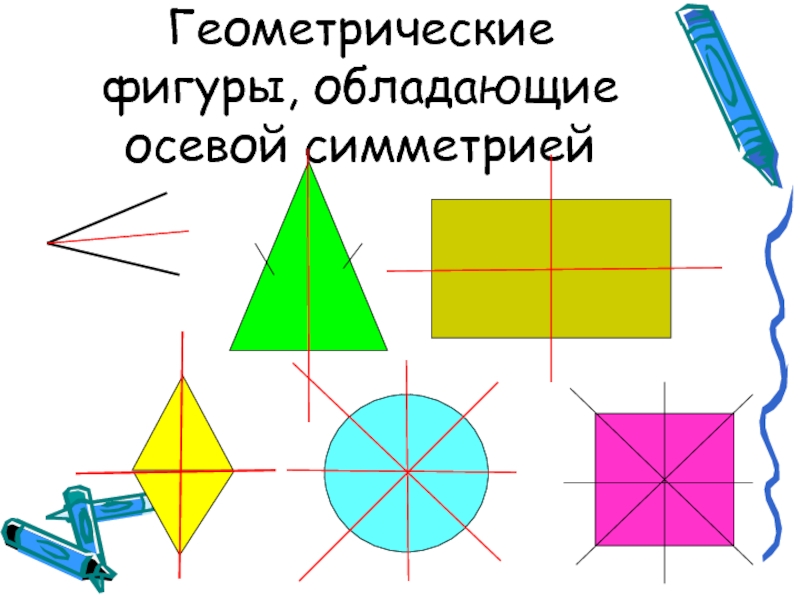
- 7. Геометрические фигуры, обладающие осевой симметрией
- 8. Геометрические фигуры, не обладающие осевой симметрией.ПараллелограммРазносторонний (произвольный) треугольник
- 9. Объекты, обладающие осевой симметрией
- 10. Но мы конечно должны понимать, что абсолютной
- 11. Сколько осей симметрии имеет:ОтрезокПрямаяЛучАВаОЕ однамножествоНи однойЗадачи:
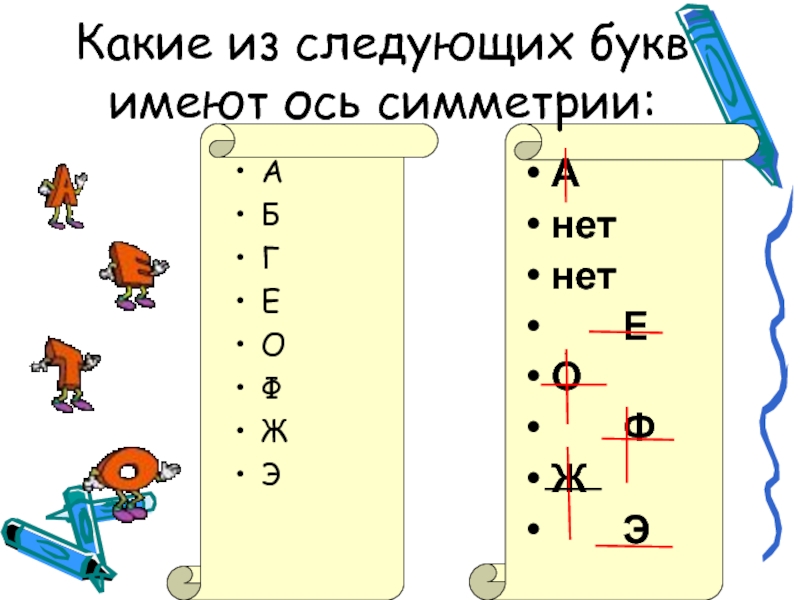
- 12. Какие из следующих букв имеют ось симметрии:АБГЕОФЖЭАнетнет ЕО ФЖ Э
- 13. Центральная симметрия
- 14. Две точки А и А1 называются симметричными
- 15. Являются ли точки симметричными относительно данной точкиРисунок 1Рисунок 2Рисунок 3М1ВВ1ОМАА1ОС
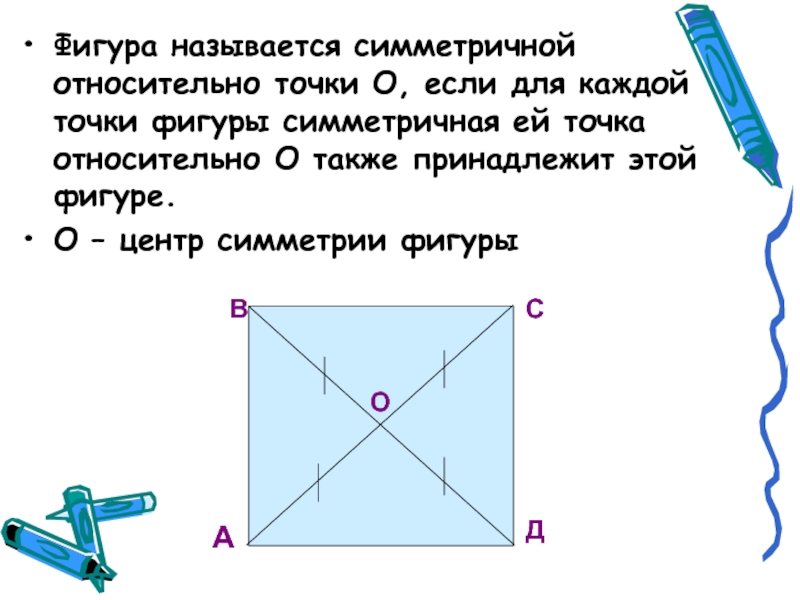
- 16. Фигура называется симметричной относительно точки О, если
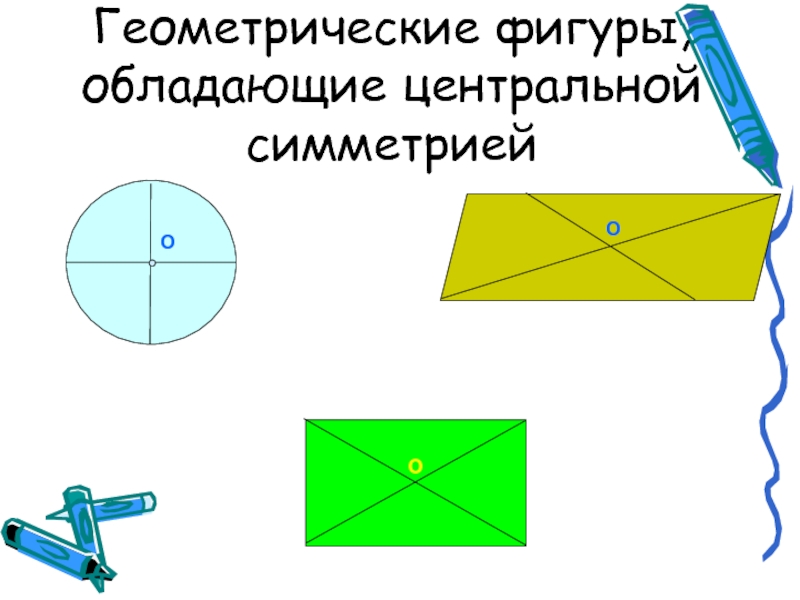
- 17. Геометрические фигуры, обладающие центральной симметриейООО
- 18. Фигуры, не обладающие центральной симметрией.Разносторонний (произвольный) треугольник.
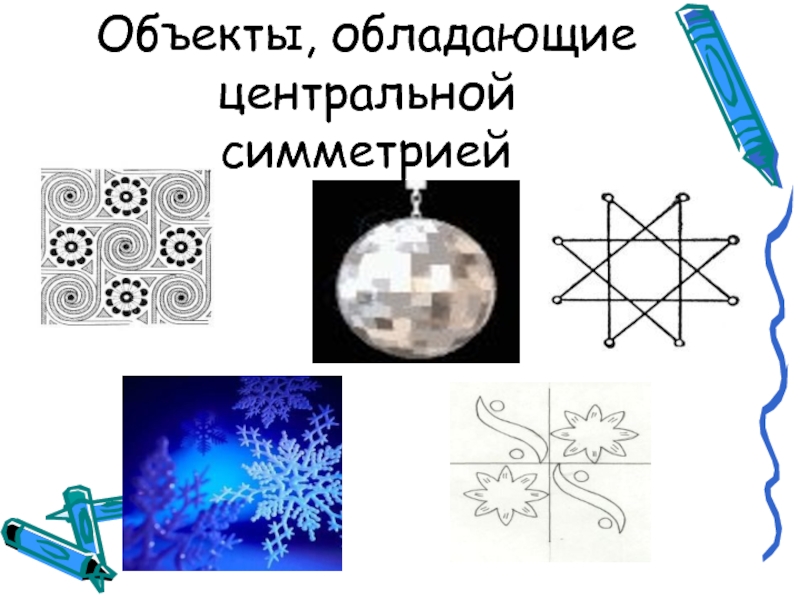
- 19. Объекты, обладающие центральной симметрией
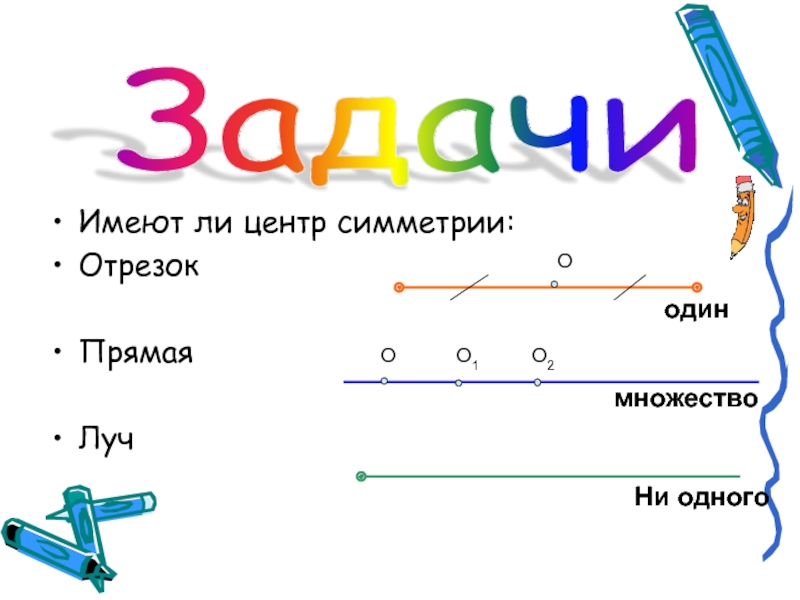
- 20. Имеют ли центр симметрии:ОтрезокПрямаяЛучЗадачи ОодинмножествоНи одногоОО1О2
- 21. Какие из следующих букв имеют центр симметрииАОМХКНнет
- 22. На основании выше изложенного можно
Выяснить, что же такое симметрия и где мы можем с ней встретиться, какие геометрические фигуры обладают симметрией и какой. (осевой или центральной). Цель:
Слайд 2Выяснить, что же такое симметрия и где мы можем с ней
встретиться, какие геометрические фигуры обладают симметрией и какой. (осевой или центральной).
Цель:
Слайд 4
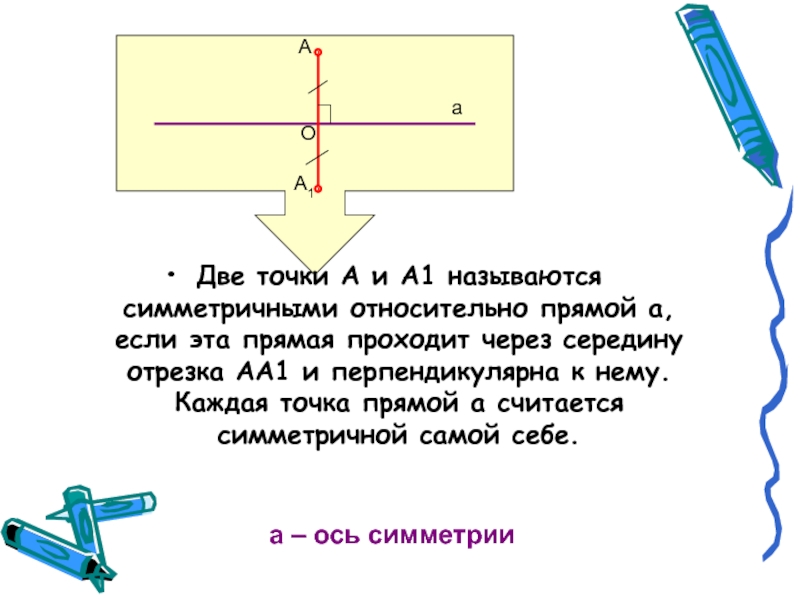
Две точки А и А1 называются симметричными относительно прямой а, если
эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.
А
А1
а
О
а – ось симметрии
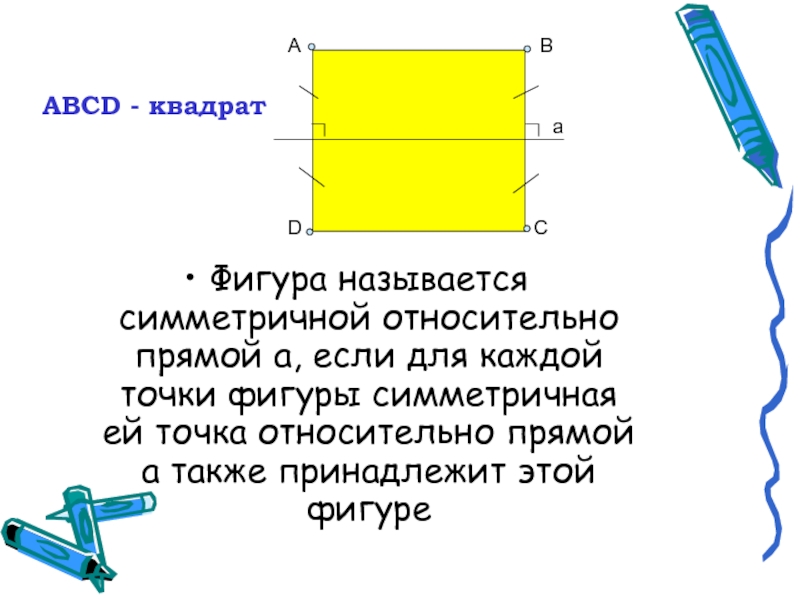
Слайд 6Фигура называется симметричной относительно прямой а, если для каждой точки фигуры
симметричная ей точка относительно прямой а также принадлежит этой фигуре
А
В
С
D
а
АВСD - квадрат
Слайд 8Геометрические фигуры, не обладающие осевой симметрией.
Параллелограмм
Разносторонний (произвольный) треугольник
Слайд 10Но мы конечно должны понимать, что абсолютной симметрии в природе быть
не может и в каждом, казалось бы симметричном объекте могут быть небольшие отклонения.
Слайд 14Две точки А и А1 называются симметричными относительно точки О, если
О – середина отрезка АА1. Точка О считается симметричной самой себе.
О - центр симметрии
О - центр симметрии
А
О
А1
Слайд 15Являются ли точки симметричными относительно данной точки
Рисунок 1
Рисунок 2
Рисунок 3
М1
В
В1
О
М
А
А1
О
С
Слайд 16Фигура называется симметричной относительно точки О, если для каждой точки фигуры
симметричная ей точка относительно О также принадлежит этой фигуре.
О – центр симметрии фигуры
О – центр симметрии фигуры
А
В
С
Д
О
Слайд 22 На основании выше изложенного можно сделать вывод, что симметрия
окружает нас везде. Даже буквы обладают симметрией!
Вывод: