- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
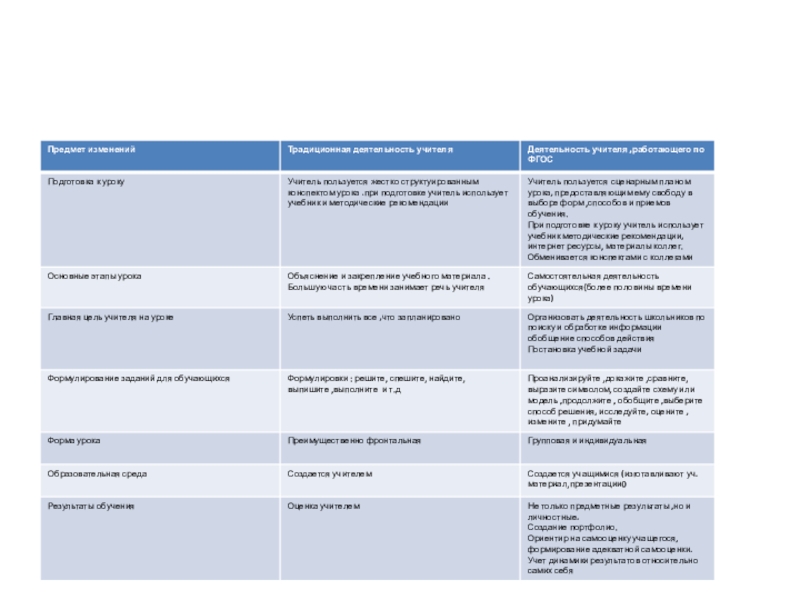
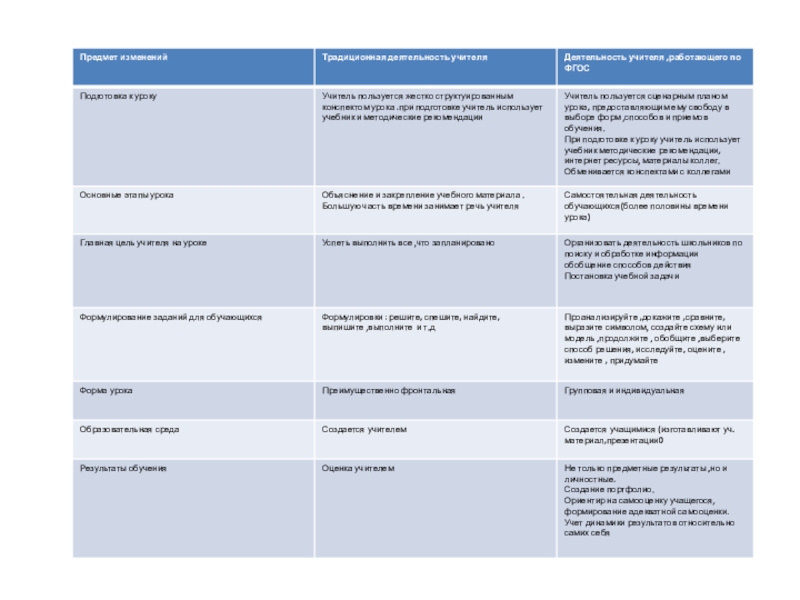
Презентация, доклад на тему Современные образовательные технологии ,используемые в рамках ФГОС на уроках математики
Содержание
- 1. Современные образовательные технологии ,используемые в рамках ФГОС на уроках математики
- 2. Реализация современныех образовательных технологиий в рамках ФГОС.
- 3. Методологическая основа ФГОСМетодологической основой ФГОС является системно-деятельностный
- 4. Деятельностный подход- это подход к организации обучения
- 5. Слайд 5
- 6. ТЕХНОЛОГИЯ (от греч. téchne — искусство, мастерство,
- 7. Педагогическая технология - это такое построение деятельности
- 8. Образовательная технология:легко вписывается в учебный процесс;позволяет достигать
- 9. обеспечивает доброжелательность по отношению к учителю и
- 10. Критерии технологичностиОбразовательная технология должна удовлетворять основным требованиям (критерии технологичности):КонцептуальностьСистемностьУправляемостьЭффективностьВоспроизводимость
- 11. Технологии:-развивающее обучение;-проблемное обучение;-разноуровневое обучение;-коллективная система обучения (КСО);-технология
- 12. Виды деятельности на уроках математики Главным требованием
- 13. Слайд 13
- 14. Сегодня обществу нужны творческие личности, которые могут
- 15. Урок был и остается одной из основных
- 16. Типы уроков.
- 17. Исследовательская деятельность Учебно-исследовательская деятельность – это деятельность,
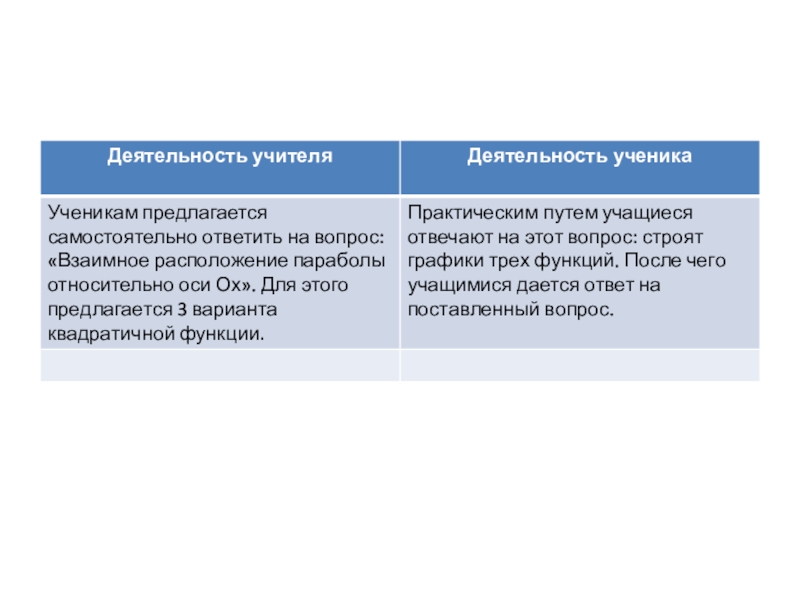
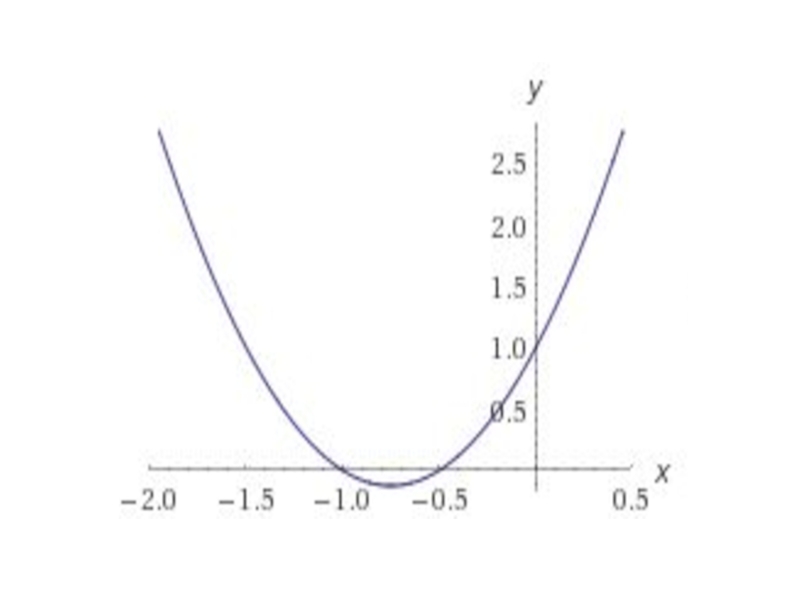
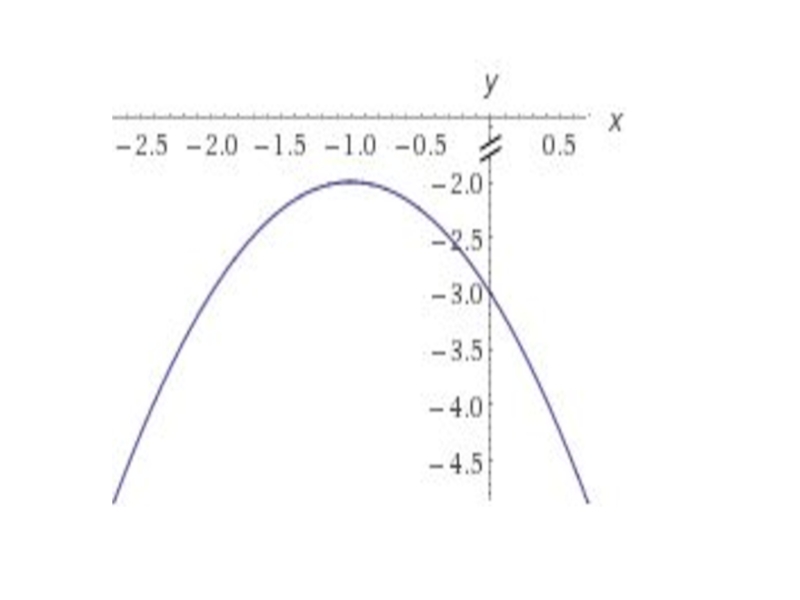
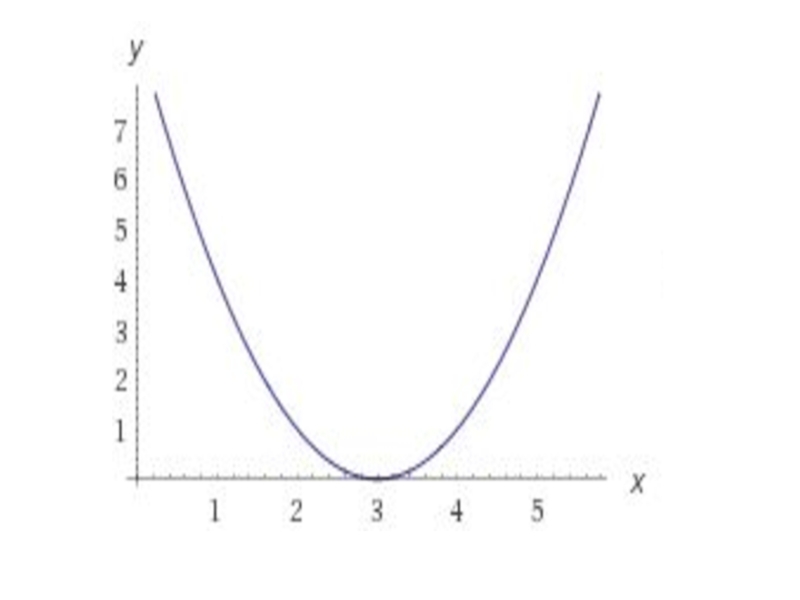
- 18. Урок алгебры в 8- классе. Тема урока: «Квадратичная функция».
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Проблемное обучение Проблемное обучение -
- 24. Проблемное обучениеМетодические приемы создания проблемных ситуаций:- учитель
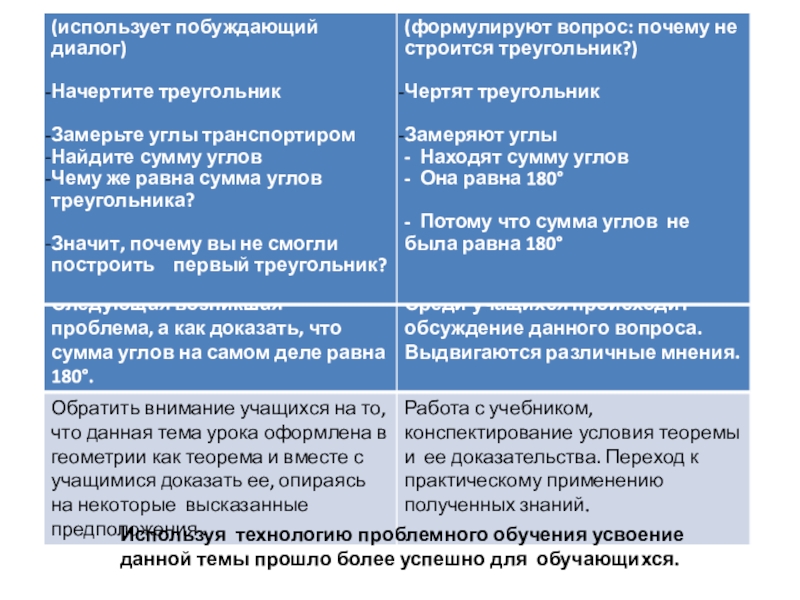
- 25. Урок геометрии в 7 классе. Тема урока: «Сумма углов треугольника»
- 26. Используя технологию проблемного обучения усвоение данной темы прошло более успешно для обучающихся.
- 27. Практическое применение.Можно привести немало примеров применения квадратичной
Слайд 1«Если человек в школе не научится творить, то и в жизни
Л.Н.Толстой
Слайд 3Методологическая основа ФГОС
Методологической основой ФГОС является системно-деятельностный подход, который нацелен на
Слайд 4Деятельностный подход- это подход к организации обучения , в котором на первый
Слайд 6ТЕХНОЛОГИЯ (от греч. téchne — искусство, мастерство, умение и греч. logos
Слайд 7Педагогическая технология -
это такое построение деятельности учителя, в котором входящие
Слайд 8Образовательная технология:
легко вписывается в учебный процесс;
позволяет достигать поставленные программой и стандартом
обеспечивает внедрение основных направлений педагогической стратегии: гуманизации, гуманитаризации образования и личностно-ориентированного подхода;
обеспечивает интеллектуальное развитие детей, их самостоятельность;
Слайд 9обеспечивает доброжелательность по отношению к учителю и друг к другу;
отличительной чертой
четкая ориентация на развитие творческой деятельности.
Слайд 10Критерии технологичности
Образовательная технология должна удовлетворять основным требованиям (критерии технологичности):
Концептуальность
Системность
Управляемость
Эффективность
Воспроизводимость
Слайд 11Технологии:
-развивающее обучение;
-проблемное обучение;
-разноуровневое обучение;
-коллективная система обучения (КСО);
-технология решения изобретательских задач (
-исследовательские методы обучения;
-проектные методы обучения;
-технология « дебаты»;
-технологию модульного и блочно- модульного обучения;
-лекционно – семинарско - зачетная система обучения;
-технология развития «критического мышления»;
-технология использования в обучении игровых методов: ролевых, деловых и других видов обучающих игр;
-обучение в сотрудничестве ( командная, групповая работа);
-информационно – коммуникационные технологии;
-здоровье сберегающие технологии;
- систему инновационной оценки « портфолио»;
- технологию дистанционного обучения
технология мастерских
групповое обучение
Слайд 12Виды деятельности на уроках математики
Главным требованием при обучении математике становится
Слайд 14Сегодня обществу нужны творческие личности, которые могут быть активными строителями жизни.
Слайд 15Урок был и остается одной из основных форм обучения. Современный урок
Слайд 17Исследовательская деятельность
Учебно-исследовательская деятельность – это деятельность, направленная на обучение учащихся алгоритму
Этапы построения учебного исследования:
Постановка проблемы
Постановка целей и задач исследования
Формулировка рабочей гипотезы
Изучение теоретического материала
Подбор и освоение методик исследования
Сбор материала
Анализ и обобщение собранного материала
Представление результатов работы
Слайд 23Проблемное обучение
Проблемное обучение -
это организация учебных занятий, которая
Результат проблемного обучения:
Творческое овладение знаниями, навыками, умениями и развитие мыслительных способностей.
Слайд 24Проблемное обучение
Методические приемы создания проблемных ситуаций:
- учитель подводит школьников к противоречию
- сталкивает противоречия в практической деятельности;
- излагает различные точки зрения на один и тот же вопрос;
- предлагает классу рассмотреть явление с различных позиций (например, командира, юриста, финансиста, педагога);
- побуждает обучаемых делать сравнения, обобщения, выводы из ситуации, сопоставлять факты;
- ставит конкретные вопросы (на обобщение, обоснование, конкретизацию, логику рассуждения);
- определяет проблемные теоретические и практические задания (например: исследовательские);
- ставит проблемные задачи (например: с недостаточными или избыточными исходными данными, с неопределенностью в постановке вопроса, с противоречивыми данными, с заведомо допущенными ошибками, с ограниченным временем решения).
Слайд 26Используя технологию проблемного обучения усвоение данной темы прошло более успешно для
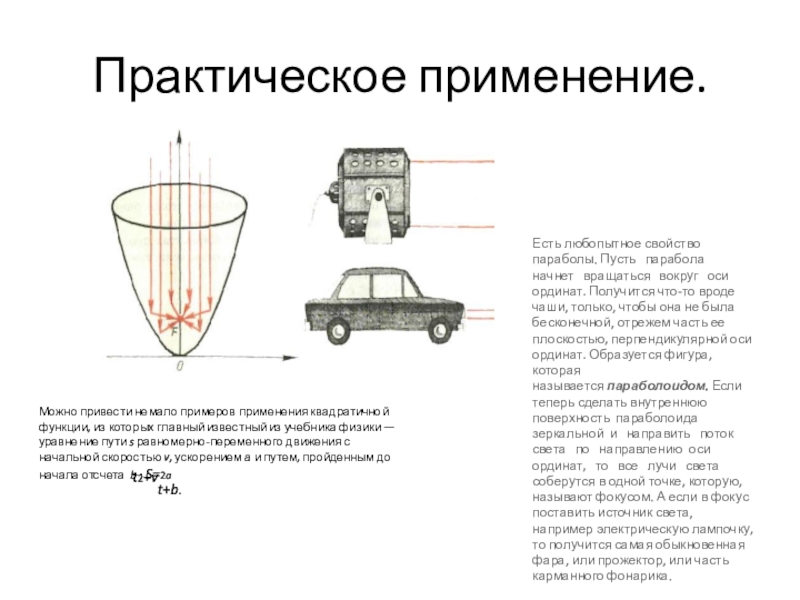
Слайд 27Практическое применение.
Можно привести немало примеров применения квадратичной функции, из которых главный
t2+v
t+b.
Есть любопытное свойство параболы. Пусть парабола начнет вращаться вокруг оси ординат. Получится что-то вроде чаши, только, чтобы она не была бесконечной, отрежем часть ее плоскостью, перпендикулярной оси ординат. Образуется фигура, которая называется параболоидом. Если теперь сделать внутреннюю поверхность параболоида зеркальной и направить поток света по направлению оси ординат, то все лучи света соберутся в одной точке, которую, называют фокусом. А если в фокус поставить источник света, например электрическую лампочку, то получится самая обыкновенная фара, или прожектор, или часть карманного фонарика.