- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Соответствия между множествами
Содержание
- 1. Соответствия между множествами
- 2. Содержание
- 3. Слайд 3
- 4. Георг Кантор (1845—1918) — немецкий математик,
- 5. ГЕОРГ КАНТОР
- 6. В 1867 окончил Берлинский университет. Кантор разработал
- 7. В основе теории множеств лежит понятие множества,
- 8. Рассматривая вопрос о соотношениях между множествами отмечают
- 9. 2. Множества А и В имеют общие
- 10. Не все элементы множества А принадлежат множеству
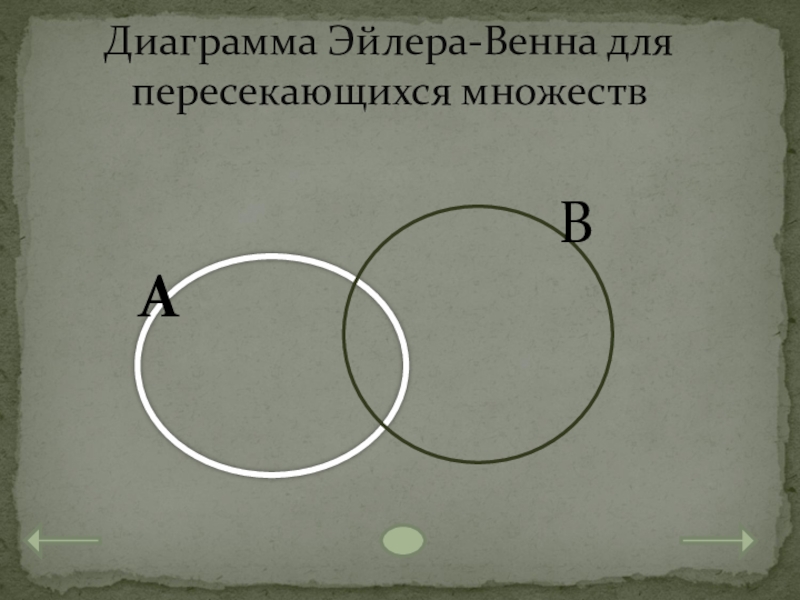
- 11. Диаграмма Эйлера-Венна для пересекающихся множествАВ
- 12. Все элементы множества А принадлежат множеству В,
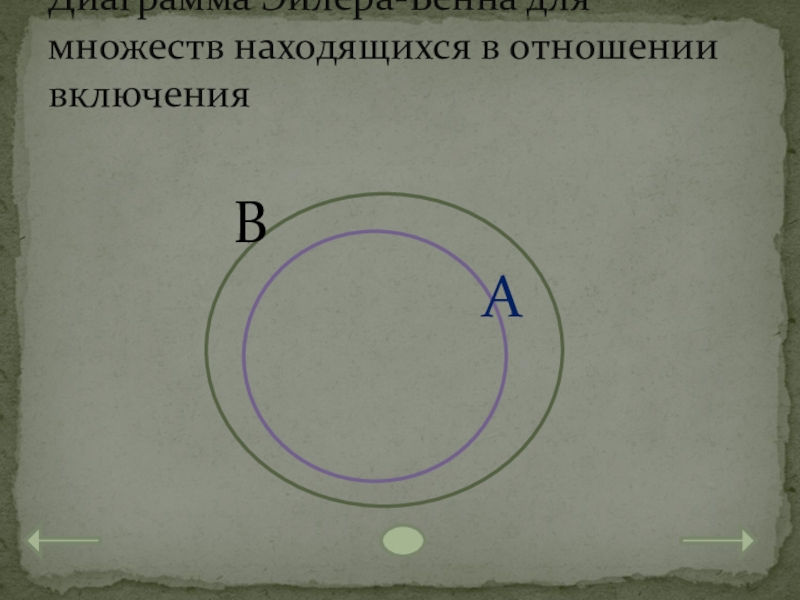
- 13. Диаграмма Эйлера-Венна для множеств находящихся в отношении включенияВА
- 14. Определение включения:Множество А называется подмножеством (или частью)
- 15. 1.РефлексивностьА А, то есть всякое
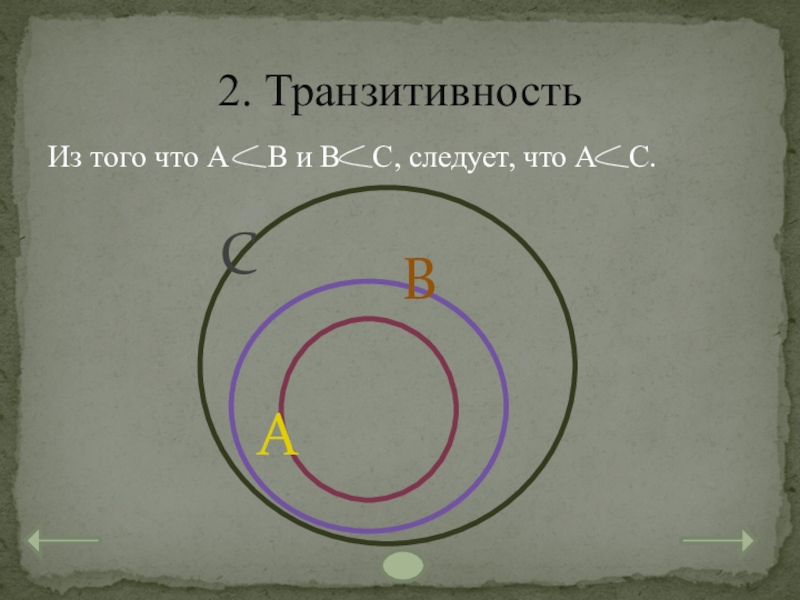
- 16. Из того что А В
- 17. Для всякого множества А справедливо включение
- 18. Все элементы множества В принадлежат множеству
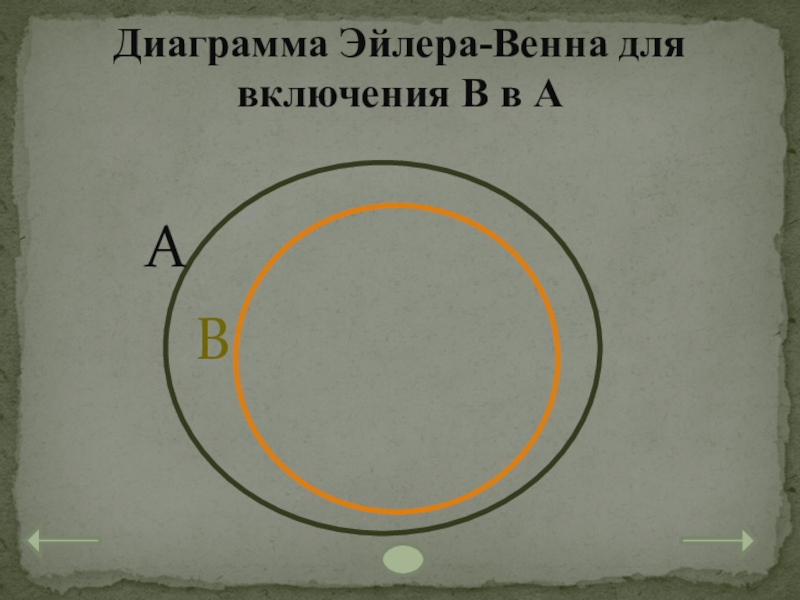
- 19. Диаграмма Эйлера-Венна для включения В в А
- 20. Все элементы множества А принадлежат множеству
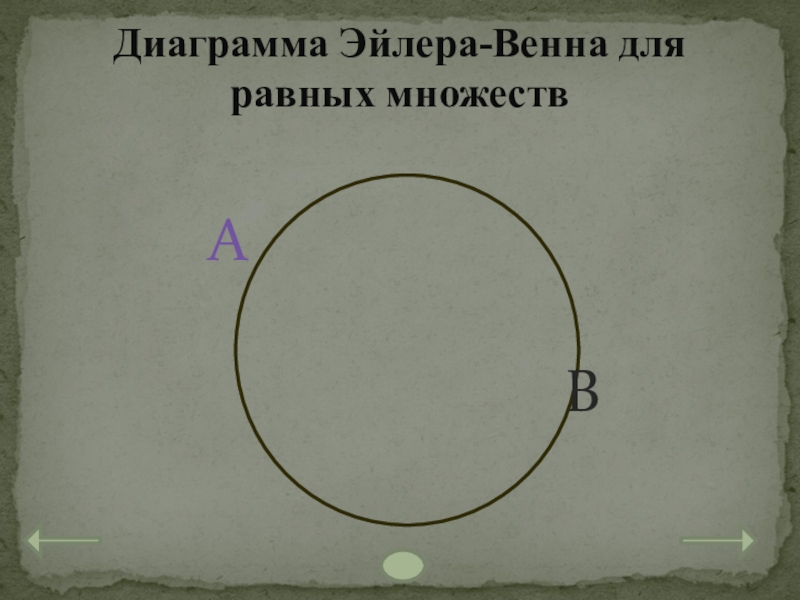
- 21. Диаграмма Эйлера-Венна для равных множеств
- 22. 1. Рефлексивность: А = А, то есть
- 23. Множество, относительно которого все множества, рассматриваемые в
- 24. Объединение множествОбъединением множеств А и В называется
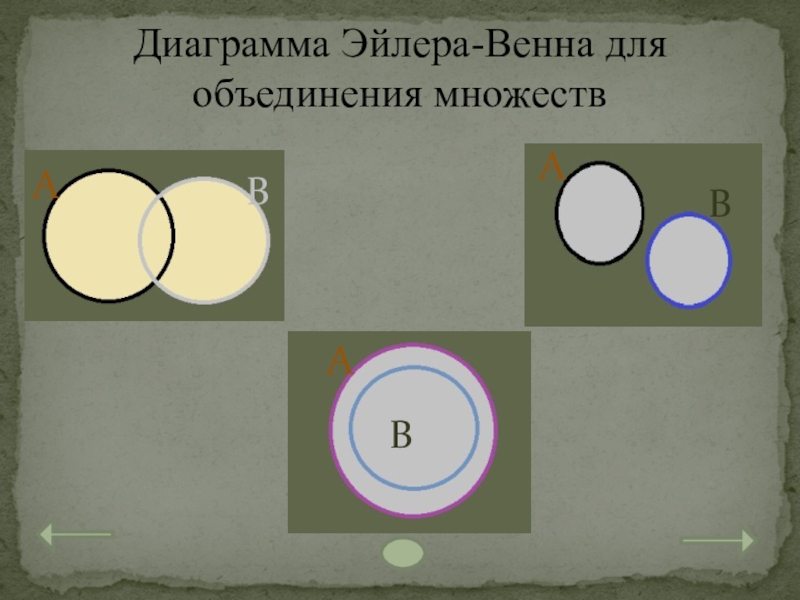
- 25. Диаграмма Эйлера-Венна для объединения множествАВАВАВ
- 26. Пересечение множествПересечением множеств А и В называется
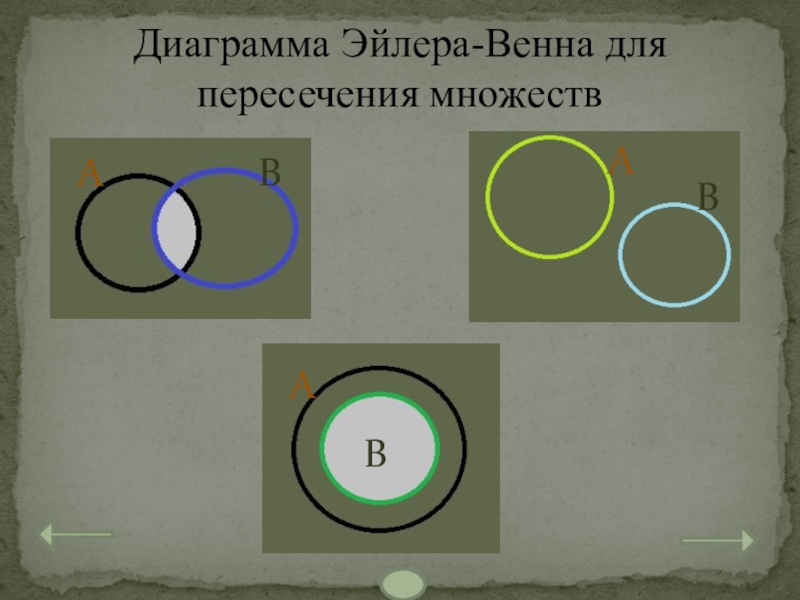
- 27. Диаграмма Эйлера-Венна для пересечения множествАААВВВ
- 28. 1. А U В = В U
- 29. 1. A U A = A2. A
- 30. Разностью множеств А и В называется множество,
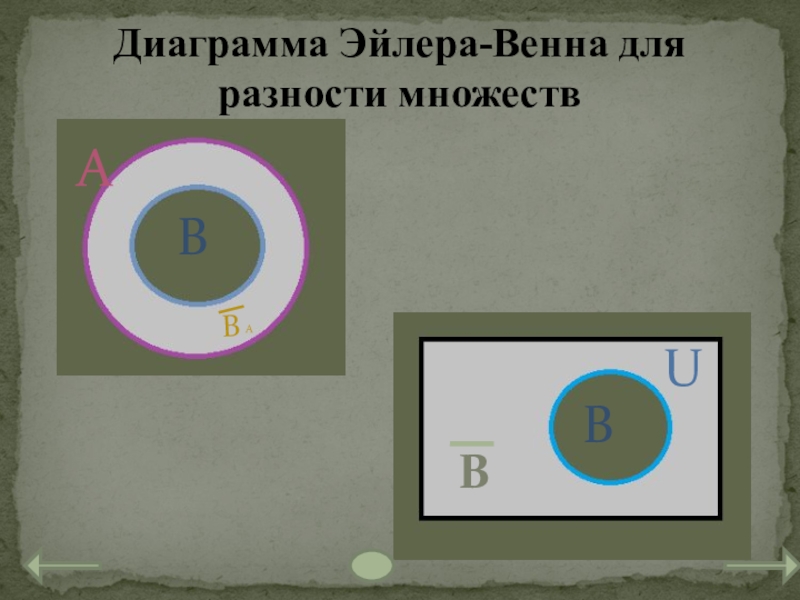
- 31. Диаграмма Эйлера-Венна для разности множествАВВАUВB
- 32. 1. Ø = U;2. U = Ø;3.
- 33. Классификацией или разбиением множества на классы называется
- 34. Декартовым произведением двух непустых множеств А и
- 35. 1. Если А ≠ В, то А
Слайд 4 Георг Кантор (1845—1918) — немецкий математик, логик, теолог, создатель теории
Создатель теории множеств
Слайд 6В 1867 окончил Берлинский университет. Кантор разработал теорию бесконечных множеств (теорию
Слайд 7В основе теории множеств лежит понятие множества, согласно Кантору: « Множество
Другими словами, множество – это совокупность предметов, сама рассматриваемая как один предмет.
Например: множество натуральных чисел N, множество действительных чисел R.
Понятие множества
Слайд 8Рассматривая вопрос о соотношениях между множествами отмечают две возможности:
1. Множества А
у ϵ А.
Соответствия между множествами
А
В
Слайд 92. Множества А и В имеют общие элементы, т.е. существуют такие
При этом возможны следующие четыре случая отношений между ними.
Слайд 10Не все элементы множества А принадлежат множеству В, и не все
Например: А - множество натуральных делителей числа 72, а В - множество натуральных делителей числа 56.
1. Пересечение множеств
Слайд 12Все элементы множества А принадлежат множеству В, но множество В может
Например: А – множество чисел, кратных 4, а множество В – чисел кратных 2.
2. Включение
Слайд 14Определение включения:
Множество А называется подмножеством (или частью) множества В, если каждый
Обозначают включение символом А В и читают «А включается в В» или «А – подмножество В»
Слайд 151.Рефлексивность
А А, то есть всякое множество включается в себя,
Свойства отношения включения:
А
Слайд 17Для всякого множества А справедливо включение Ø А.
Само множество А и пустое множество Ø называют несобственными подмножествами множества А. Все остальные подмножества множества А называются собственными
3. Включение Ø А
Слайд 18 Все элементы множества В принадлежат множеству А, но множество А
3. Включение В в А
Слайд 20 Все элементы множества А принадлежат множеству В, и элементы множества
Два множества А и В называются равными если они состоят из одних и тех же элементов.
4. Равные множества
Слайд 221. Рефлексивность: А = А, то есть всякое множество равно самому
2. Симметричность: если А = В, то и
В = А.
3. Транзитивность: если А = В и В = С, то А = С.
Свойства отношения равенства
Слайд 23Множество, относительно которого все множества, рассматриваемые в данной задаче, являются подмножествами,
Например, множество действительных чисел R.
Универсальное множество обозначается буквой U, а на диаграммах Эйлера-Венна изображается в виде прямоугольника.
Универсальное множество
U
Слайд 24Объединение множеств
Объединением множеств А и В называется множество, состоящее из тех
Обозначают объединение множеств А и В символом
А U В.
Согласно определению объединения х ϵ А U В тогда и только тогда, когда х ϵ А или х ϵ В. Соответственно,
х ϵ А U В тогда и только тогда, когда х ϵ А и х ϵ В.
Операции над множествами
Слайд 26Пересечение множеств
Пересечением множеств А и В называется множество, состоящее из тех
Пересечение множеств А и В обозначают символом
А В.
Как следует из определения пересечения множеств,
х ϵ А В тогда и только тогда, когда х ϵ А и х ϵ В.
Соответственно, х ϵ А В тогда и только тогда, когда
х ϵ А или х ϵ В.
U
U
U
Слайд 281. А U В = В U А – коммутативность объединения;
2.
3. А U (B U C) = (A U B) U C – ассоциативность объединения;
4. A (B C) = (A B) C – ассоциативность пересечения;
5. A (BUC) = (A B)U(A C) – дистрибутивность пересечения относительно объединения;
6. AU(B C) = (AUB) (AUC) – дистрибутивность объединения относительно пересечения.
Свойства объединения и пересечения множеств
U
U
U
U
U
U
U
U
U
U
U
Слайд 30Разностью множеств А и В называется множество, состоящее из тех и
Разность множеств А и В обозначают символом А\В.
Согласно определению разности х ϵ А\В тогда и только тогда, когда х ϵ А и х ϵ В. Соответственно, х ϵ А\В тогда и только тогда, когда х ϵ А или х ϵ В.
Операция, при помощи которой находится разность множеств, называется вычитанием.
Если В А, то разность А\В называется дополнением множества В до А. обозначают дополнение символом ВА.
Если множество В является подмножеством универсального множества U, то дополнение В до U обозначают В.
Разность двух множеств. Дополнение
Слайд 321. Ø = U;
2. U = Ø;
3. A \ Ø =
4. A = A;
5. A ∩ A = Ø;
6. A U A = U;
7. A U B = A ∩ B;
8. A ∩ B = A U B;
9. A \ B (B ∩ C) = (A \ B) U (A \ C);
10. A \ (B U C) = (A \ B) ∩ (A \ C).
Свойства разности и дополнения
Слайд 33Классификацией или разбиением множества на классы называется представление этого множества в
Таким образом, разбиение множества М на классы К1, К2,…,Кn определяется следующими тремя условиями:
1) Ki ≠ Ø (i= 1, 2,…n);
2) Ki ∩ Kj = Ø (i, j, = 1, 2,…n; i ≠ j);
3) U Ki = M.
Разбиение множеств на классы. Классификация
i ≠ 1
n
Слайд 34Декартовым произведением двух непустых множеств А и В называется множество, состоящее
Декартово произведение множеств А и В обозначают символом А В.
Операция, с помощью которой находится декартово произведение множеств, называется декартовым умножением.
Декартово произведение множеств
Слайд 351. Если А ≠ В, то А В ≠ В
2. Если ни одно из множеств А, В и С не являются пустыми, то А (В С) ≠ (А В) С;
3. А (В U С) = (А В)U(А С);
4. (А U В) С = (А С) U (В С);
5. А (В∩С) = (А В) ∩ (А С);
6. (А ∩ В) С = (А С) ∩ (В С);
7. А (В \ С) = (А В) \ (А С);
8. (А \ В) С = (А С) \ (В С);
Свойства декартова произведения