Презентация, доклад на тему Роль математики в физике

ученицами 10 класса
ГБОУ СОШ с.Чёрный Ключ
Беловой Еленой и
Кудряшовой Ангелиной
Руководитель проекта-
Лебакина Светлана Николаевна

предметами школьного курса. Широко распространено мнение о том, что в школьном преподавании интеграция физики с математикой возможна только в классах с углубленным изучением этих предметов.

показать взаимосвязь изучаемого материала и возможность использования полученных в математике знаний для решения физических задач и наоборот.
Цель:
1) Определить сущность, функции межпредметных связей и их классификацию;
2) Показать какие понятия математики и каким образом используются в физике.
Задача№1
Показать причины, по которым знания математики необходимы.
Задача№2
Определить необходимые математические понятия для физики.
Объект исследования математические приёмы и методы, физические законы, где возможно и необходимо их применение.
Методы, применяемые в работе: общенаучные, конкретно-научные, логические.

играет математика в физике.
Принцип межпредметной связи лежит в основе изучения физики, поскольку это наука включает знания из других областей и в свою очередь необходима для их понимания. При рассмотрении многих явлений и процессов на уроках физики нужны знания по многим другим предметам, таким как математики, географии, химии, биологии и другие. Вместе с тем и для изучения этих учебных дисциплин необходимы глубокие и прочные знания физики и методов физической науки (например, применение понятий энергии и закона сохранения и превращения энергии в биологических процессах; физические явления, законы и методы в астрономии и т.д.). это значит, что в принципе межпредметных связей находит своё воплощение дифференциация и интеграция наук, которые в настоящее время развиты так хорошо.
 
Роль математики в физике сложно переоценить. Известна цитата Галилео Галилея «Математика — это язык, на котором написана книга Природы». Но только ли языком является современная математика? Работа математиков заключается в нахождении новых математических объектов и исследовании их свойств и взаимосвязей. Со времен Галилея появилось множество новых разделов математики со своим языком для описания математических объектов.

в физике.

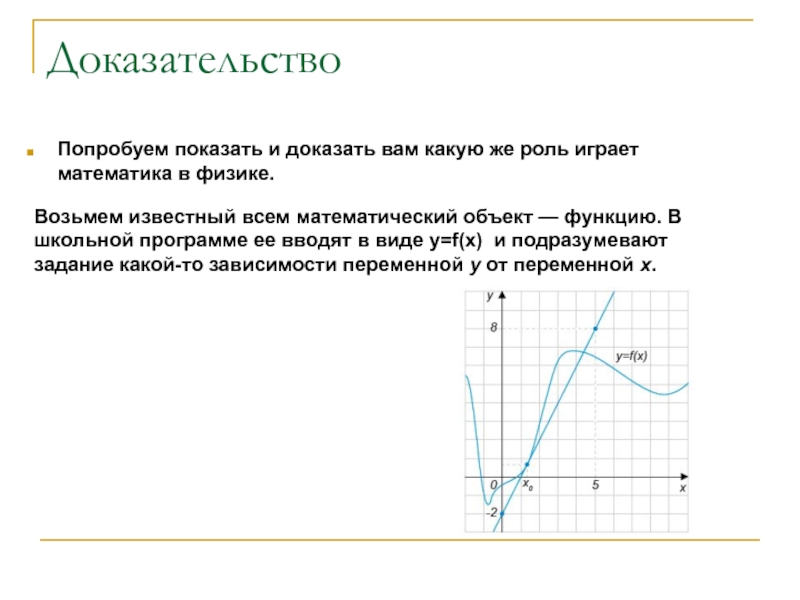
Возьмем известный всем математический объект — функцию. В школьной программе ее вводят в виде y=f(x)  и подразумевают задание какой-то зависимости переменной y от переменной x.

другое:
A→fB




А с помощью абстрактной алгебры функцию можно представить в виде оператора, а набор значений x и y считать векторами. В данном описании задание функции эквивалентно заданию матрицы оператора F^F^. Y=F^XY=F^X
А в теории возмущений, функции привычнее задавать в виде бесконечного ряда. Причем для разных областей определения функции конкретный вид ряда может отличаться.
f(x)=∑n=0∞anxn

человеческих размышлений. Математика базируется на формальной логике, для нее, например, равноправны и геометрия Эвклида, и геометрия Лобачевского, физика же должна отражать только одну реальную геометрию, существующую в природе. Но дело не только в формализме, присущем математике. Следует иметь в виду еще два обстоятельства. 
Во-первых, подтверждение выводов некоей математической теории экспериментальными фактами еще не
говорит о том, что эта математическая теория единственно верная. Те же экспериментальные факты могут быть впоследствии подтверждены и другой математической теорией, и такие примеры в физике имеются. Например, колебательные процессы одинаково успешно описываются и тригонометрическими, и экспоненциальными функциями, и методом векторных диаграмм.  Во-вторых, в физике часто применяется разложение математических функций в ряд с пренебрежением третьего и последующих членов разложения ввиду их малости. Однако, то, что на данном этапе развития физики считается пренебрежительно малым и даже просто незаметным, в дальнейшем на другом уровне развития физики может сыграть исключительно важную роль. Это красочно описано в книге Б.Грина (2004), посвященной теории суперструн. 

природе нет.
2. Движение в природе всегда связано с вращением, но это не всегда учитывается.
3.В физике обязательно соблюдение принципа причинности, тогда как в математике его соблюдение не обязательно.
4. Вне движения нет смысла говорить о пространстве и времени, а в
математике это допускается.
5. Безразмерных величин в природе нет, сам термин неверен.
6. В природе нет материальных точек, а есть физические системы (тела).
7. В физике существуют величины, записывающиеся, как произведение величин, заключенное в скобки. Сомножители этих произведений нельзя сокращать
8. В физике направлением обладает только движение,
его различные свойства и побуждающие движение
физические величины
9. В математическом методе векторных диаграмм 
вращающийся радиус-вектор не является физической
величиной.

в физике. Как можно было заметить, на эту тему не существует единой точки зрения. И чтобы хоть немного разобраться в этом вопросе «какую же роль играет математика в физике?» , мы решили провести научное исследование на эту тему.

можем с уверенностью сказать, что математика необходима в физике.
Без математического вмешательства физика не смогла бы дойти до таких известных открытий, как расчет Ньютона.

Она является специальным языком, помогающим исследовать не только окружающий нас мир, но и целую Вселенную. Математика, как фундаментальная наука, является системой различных методов, которые помогают развитию естественных наук в различных направлениях. Применение математики в физике и естественных науках очень огромно, в каждой науке есть хоть одна частица применения математики, что и было представлено в вышеуказанных примерах.