- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение математических задач с помощью кругов Эйлера
Содержание
- 1. Решение математических задач с помощью кругов Эйлера
- 2. Леонард Эйлер ИДЕАЛЬНЫЙ МАТЕМАТИК XVIII ВЕКА (к 300-летию со дня рождения)
- 3. "Письма о разных физических и
- 4. Эйлер писал тогда, что «круги очень подходят
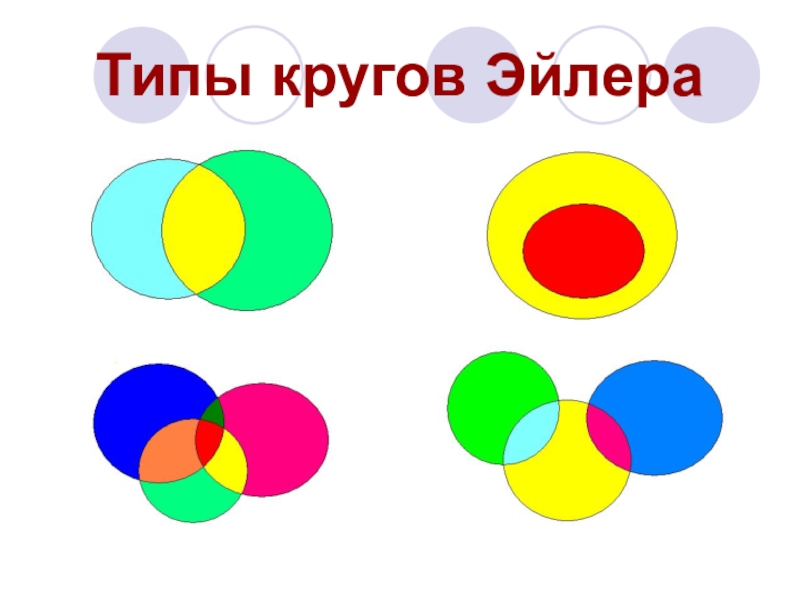
- 5. Типы кругов Эйлера
- 6. Множество чиселМножество всех действительных чисел Эйлер изобразил
- 7. Задача 1. О подругах Все мои подруги
- 8. Спортивная задачаВ футбольной команде 30 игроков, среди
- 9. Решение18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в
- 10. Задача 3В офисе работает 30 человек. 20
- 11. Решение. 1 способ. Для решения
- 12. Задача 4 В классе учится
- 13. А + Н = 34
- 14. Задача 5В магазине побывало 65 человек. Известно,
- 15. Решение Купили только ноутбуки: 35-(20-3)-(15-3)-3=4.Купили только телефоны:
- 16. Заключение. В результате работы над данной темой
- 17. 2) Любое натуральное число является элементом любого
Леонард Эйлер ИДЕАЛЬНЫЙ МАТЕМАТИК XVIII ВЕКА (к 300-летию со дня рождения)
Слайд 3 "Письма о разных физических и философических материях, написанные к
некоторой немецкой принцессе...", где появились впервые «круги Эйлера»
Слайд 4Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить
наши размышления».
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».
Слайд 6Множество чисел
Множество всех действительных чисел Эйлер изобразил с помощью этих кругов:
N-множество натуральных чисел,
Z – множество целых чисел,
Q – множество рациональных чисел,
R – множество вех действительных чисел.
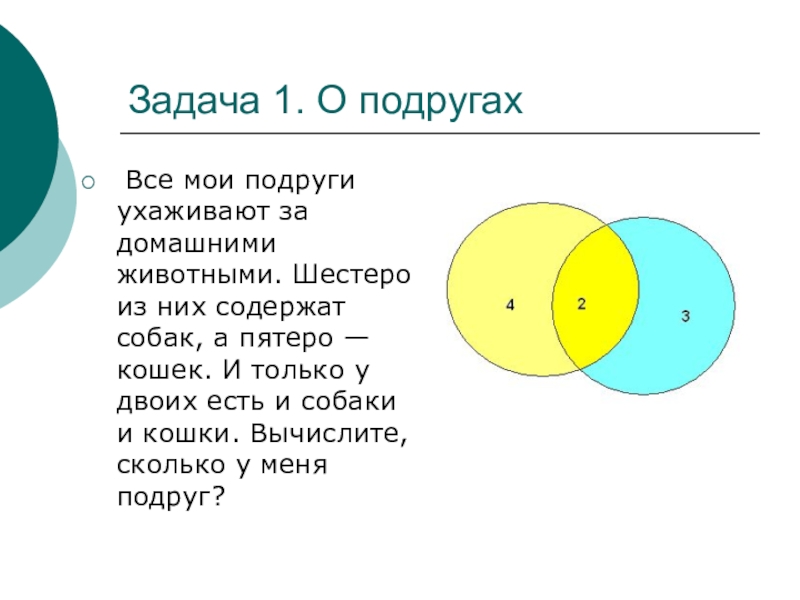
Слайд 7Задача 1. О подругах
Все мои подруги ухаживают за домашними животными.
Шестеро из них содержат собак, а пятеро — кошек. И только у двоих есть и собаки и кошки. Вычислите, сколько у меня подруг?
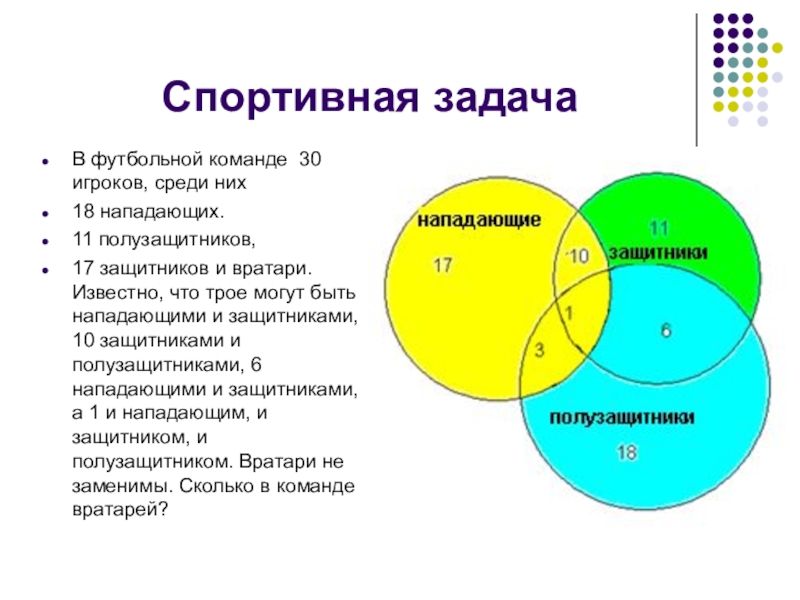
Слайд 8Спортивная задача
В футбольной команде 30 игроков, среди них
18 нападающих.
11
полузащитников,
17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде вратарей?
17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде вратарей?
Слайд 9Решение
18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов.
Значит вратарей будет 30-28=2. Ответ: 2 вратаря.
Слайд 10Задача 3
В офисе работает 30 человек. 20 из них каждый день
пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?
Слайд 11
Решение. 1 способ. Для решения опять воспользуемся кругами Эйлера:
Пусть х человек
пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро:
20 − (12 − х) − (10 − х) − х = х − 2
Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:
Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3.
2 способ. А можно эту задачу решить задачу другим способом:
20+15+23-10-12-9+х=30, 27+х=30, х=3.
20 − (12 − х) − (10 − х) − х = х − 2
Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:
Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3.
2 способ. А можно эту задачу решить задачу другим способом:
20+15+23-10-12-9+х=30, 27+х=30, х=3.
Слайд 12Задача 4
В классе учится 40 человек. Каждый из
них изучает не менее одного иностранного языка: английский, немецкий, французский. 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно два языка — английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?
Слайд 13
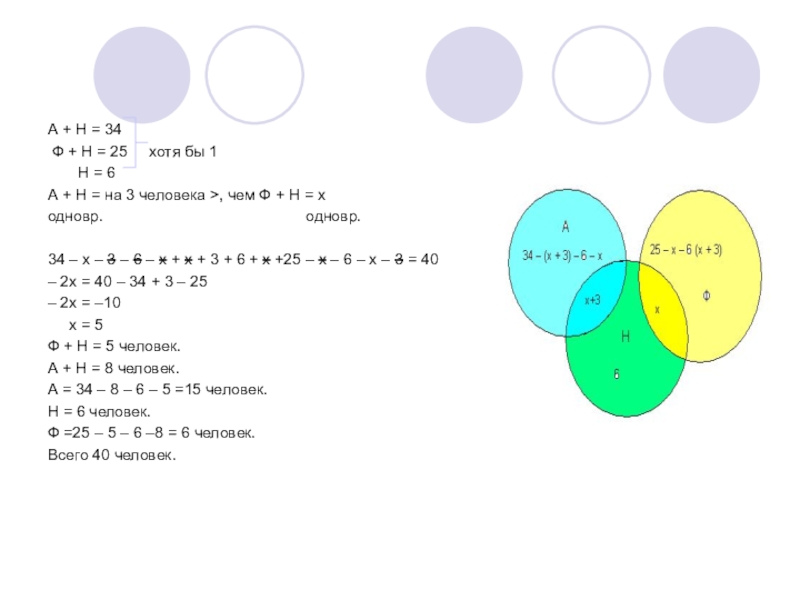
А + Н = 34
Ф + Н =
25 хотя бы 1
Н = 6
А + Н = на 3 человека >, чем Ф + Н = х
одновр. одновр.
34 – х – 3 – 6 – х + х + 3 + 6 + х +25 – х – 6 – х – 3 = 40
– 2х = 40 – 34 + 3 – 25
– 2х = –10
х = 5
Ф + Н = 5 человек.
А + Н = 8 человек.
А = 34 – 8 – 6 – 5 =15 человек.
Н = 6 человек.
Ф =25 – 5 – 6 –8 = 6 человек.
Всего 40 человек.
Н = 6
А + Н = на 3 человека >, чем Ф + Н = х
одновр. одновр.
34 – х – 3 – 6 – х + х + 3 + 6 + х +25 – х – 6 – х – 3 = 40
– 2х = 40 – 34 + 3 – 25
– 2х = –10
х = 5
Ф + Н = 5 человек.
А + Н = 8 человек.
А = 34 – 8 – 6 – 5 =15 человек.
Н = 6 человек.
Ф =25 – 5 – 6 –8 = 6 человек.
Всего 40 человек.
Слайд 14Задача 5
В магазине побывало 65 человек. Известно, что они купили 35
ноутбуков, 36 телефонов, 37 навигаторов. 20 из них купили и
ноутбук и телефон, 19 - и телефон, и навигатор, 15- ноутбук и навигатор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
ноутбук и телефон, 19 - и телефон, и навигатор, 15- ноутбук и навигатор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
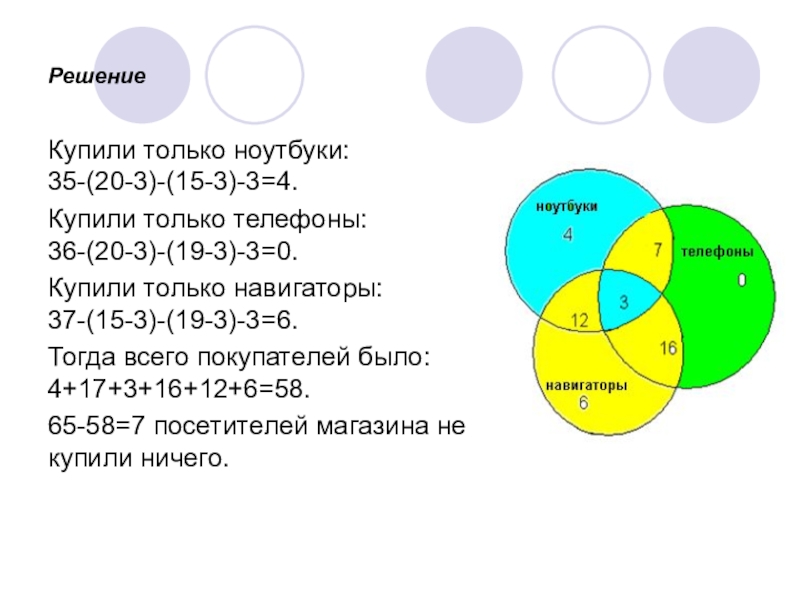
Слайд 15Решение
Купили только ноутбуки: 35-(20-3)-(15-3)-3=4.
Купили только телефоны: 36-(20-3)-(19-3)-3=0.
Купили только навигаторы: 37-(15-3)-(19-3)-3=6.
Тогда
всего покупателей было: 4+17+3+16+12+6=58.
65-58=7 посетителей магазина не купили ничего.
65-58=7 посетителей магазина не купили ничего.
Слайд 16Заключение.
В результате работы над данной темой я пришла к следующим
выводам:
1) Все множества чисел связаны между собой так, что каждое следующее, более объемное, включает в себя предыдущее множество полностью;
1) Все множества чисел связаны между собой так, что каждое следующее, более объемное, включает в себя предыдущее множество полностью;
Слайд 17
2) Любое натуральное число является элементом любого следующего множества.
3) Применение
кругов Эйлера (диаграмм Эйлера-Венна) позволяет решить задачи новым, более наглядным способом