- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение квадратных уравнений
Содержание
- 1. Решение квадратных уравнений
- 2. Квадратным уравнением называется уравнение вида ах2+bх+с=0, где
- 3. Являются ли ниже перечисленные уравнения квадратными?48х2-х3+5=0
- 4. Вы совершенно правы
- 5. Не верно, подумайте ещё
- 6. Вы совершенно правы, продолжим
- 7. Квадратные уравнения можно решать несколькими способами:
- 8. Решение квадратных уравнений графическим способом.Решать квадратные уравнения
- 9. Вы совершенно правы
- 10. Не верно, подумайте ещё
- 11. Попробуйте решить самостоятельно и выбрать правильный ответ.1.
- 12. Вы совершенно правы, продолжим
- 13. Решение квадратных уравнений выделение квадрата двучлена.Пример: х2-8х+15=0
- 14. Попробуйте решить самостоятельно и выбрать правильный ответ.1.
- 15. Вы совершенно правы
- 16. Не верно, подумайте ещё
- 17. Вы совершенно правы, продолжим
- 18. Решение квадратных уравнений по формуле. ах2+bх+с=0
- 19. Попробуйте решить самостоятельно и выбрать правильный ответ.1.
- 20. Вы совершенно правы
- 21. Не верно, подумайте ещё
- 22. Вы совершенно правы, продолжим
- 23. Решение квадратных уравнений по теореме обратной теореме
- 24. Попробуйте решить самостоятельно и выбрать правильный ответ.1.
- 25. Вы совершенно правы
- 26. Не верно, подумайте ещё
- 27. Вы совершенно правы, продолжим
- 28. Ваши дальнейшие действияХотите повторить тренировку ?Задания для самоконтроляХотите закончить тренировку?Список использованной литературы
- 29. Виет Франсуа (1540, Фонтене-ле-Конт, - 13.12.1603, Париж)
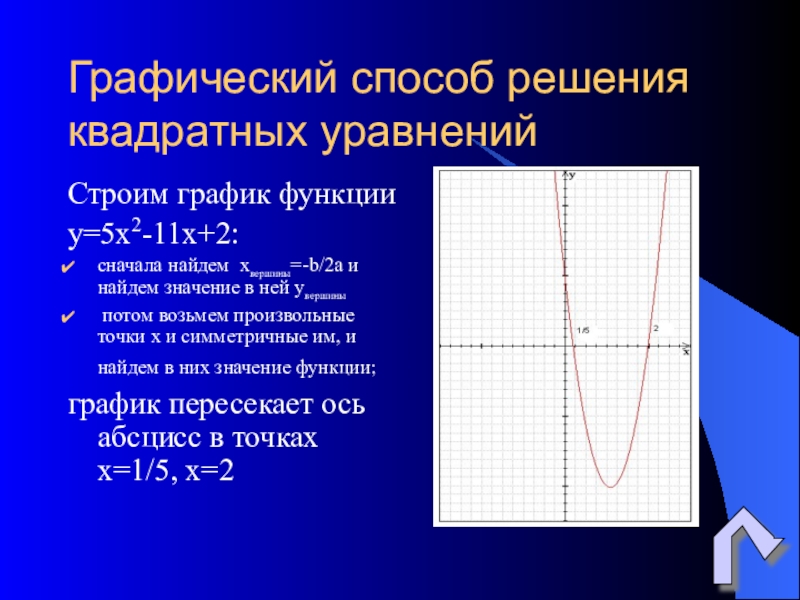
- 30. Графический способ решения квадратных уравненийСтроим график функции
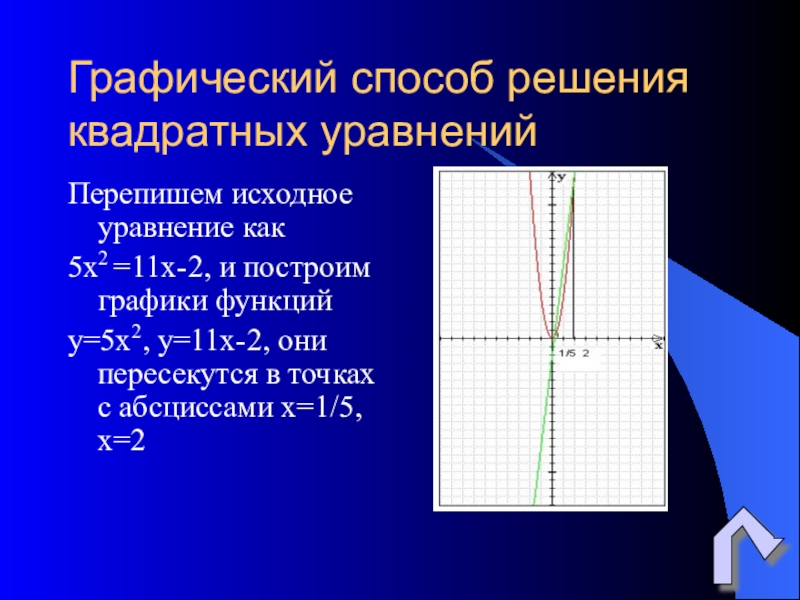
- 31. Графический способ решения квадратных уравненийПерепишем исходное уравнение
- 32. О проектеДанный проект был создан учениками девятого
- 33. Список использованной литературыБольшая советская энциклопедияМордкович А. Г.
- 34. Теорема Виета для корней квадратного уравнения* *
- 35. Задания для самоконтроля Являются ли следующие уравнения квадратными? -х2=07х2-13=01-15х=00х2-14х+5=0-5х+12х2=0Ответы. Решить уравнения, удобным способом:х2-4х+3=05х2+3х-8=05х2+14х-3=035х2+2х-1=025=26х-х23х2-8х+5=0у2=4у+96у2-10у+25=0Ответы.
- 36. Ответы.ДаДаНетНетДах1=1; х2=3х1=-1,6; х2=1х1=-3; х2=0,2х1=-0,2; х2=1/7х1=1; х2=25х1=1; х2=5/3 у1=-8; у2=12 у=5
- 37. ТЕСТ 1ОТВЕТЫ:
- 38. Ответы на тест 1:ВББАГГБ
- 39. ТЕСТ 2ОТВЕТЫ:
- 40. Ответы на тест 2:ВБАГБАБ
- 41. Неполные квадратные уравнения Если в квадратном уравнение
- 42. Способы решения неполных квадратных уравнений
- 43. Неполное квадратное уравнение при b=0Уравнение примет вид
- 44. Неполное квадратное уравнение при c=0Уравнение примет вид
- 45. Неполное квадратное уравнение при b=0, c=0Уравнение примет
- 46. Решение неполных квадратных уравненийРешить 4x2-9=0
- 47. Вы совершенно правы
- 48. Не верно, подумайте ещё
- 49. Вы совершенно правы, продолжим
- 50. Не верно, подумайте ещё
- 51. Не верно, подумайте ещё
- 52. Не верно, подумайте ещё
- 53. Не верно, подумайте ещё
- 54. Не верно, подумайте ещё
- 55. Презентацию создали:Ученики 9 «А» класса 588 школы
Слайд 2Квадратным уравнением называется уравнение вида ах2+bх+с=0, где х – переменная, а,
Что такое неполные квадратные уравнения?
Слайд 3Являются ли ниже перечисленные уравнения квадратными?
48х2-х3+5=0
2,1х2-2х+2/3=0 Да-2х+2/3=0 Да Нет
1-12х=0 Да1-12х=0 Да Нет
7х2-4=0 Да-4=0 Да Нет
Слайд 7Квадратные уравнения можно решать несколькими способами:
Графическим способом
Выделением квадрата двучлена
По формуле
По обратной теореме Виета
ТЕСТ 2
Слайд 8Решение квадратных уравнений графическим способом.
Решать квадратные уравнения графически можно по-разному. Например:
Построить график функции y=5х2-11х+2, найти абсциссы точек пересечения с осью х, они и будут корнями исходного уравнения.
Записать исходное уравнение, как 5х2 =11х-2, и построить графики функций y=5х2, y=11х-2, после этого найти абсциссы точек пересечения графиков, которые и будут являться корнями исходного уравнения.
И в том и другом случае ответ 1/5, 2, но его можно получить лишь приближенно.
Слайд 11Попробуйте решить самостоятельно и выбрать правильный ответ.
1. х2+9х-22=0
-1,5; 11 8/3; 2
-11; 1,5 6; 8
-22; 3 -6; -8
А
А
В
В
С
С
Слайд 13Решение квадратных уравнений выделение квадрата двучлена.
Пример: х2-8х+15=0
(*) х2-2·4х+42-42+15=0
х2-2·4х+42 =42 -15
(х-4)2=1
х-4 =1 или х-4=- 1
х=5 или х=3
Ответ: 3; 5.
Формулы суммы и разности квадрата двучлена
a2+2ab+b2 = (a+b)2
a2-2ab+b2 =(a-b)2
Если к разности х2-8х прибавить число 16, то полученное выражение можно записать в виде квадрата двучлена (х-4)2, прибавим и вычтем 42 и получим (*), после преобразований найдем корни
Слайд 14Попробуйте решить самостоятельно и выбрать правильный ответ.
1. х2+12х+20=0
-2; -10 -6; 1
2; 10 -1; 6
Нет корней Нет корней
А
В
С
А
В
С
Слайд 18Решение квадратных уравнений по формуле.
ах2+bх+с=0 D=b2-4ac
Если
Если D=0, то уравнение имеет один корень
Если D<0, то уравнение не имеет корней
Пример:
Решить 3х2-14х+16=0
D=196-4⋅3⋅16=196-192=4
х1=(14-2)/6=2
х2=(14+2)/6=8/3
Ответ: 2; 8/3.
Слайд 19Попробуйте решить самостоятельно и выбрать правильный ответ.
1. 2х2+3х+1=0
-2; -1 2; 3
-1; -1/2 -2; 12
Нет корней Нет корней
А
А
В
В
С
С
Слайд 23Решение квадратных уравнений по теореме обратной теореме Виета.
(Кто такой Виет?)
Теорема: Если
Пример: х2+3х-40=0
х1+х2=-3 и х1·х2=-40
⇒ х1 =-8, х2=5
Ответ: -8; 5.
Как запомнить эту теорему?
Слайд 24Попробуйте решить самостоятельно и выбрать правильный ответ.
1. х2 -15х-16=0
-1; 16 -1,5; -2
-16; 1 1,5; 2
-15; -1 -1,5; 2
А
А
В
В
С
С
Слайд 28Ваши дальнейшие действия
Хотите повторить тренировку ?
Задания для самоконтроля
Хотите закончить тренировку?
Список использованной
Слайд 29Виет Франсуа (1540, Фонтене-ле-Конт, - 13.12.1603, Париж)
-
(Большая Советская Энциклопедия)
Слайд 30Графический способ решения квадратных уравнений
Строим график функции
y=5х2-11х+2:
сначала найдем хвершины=-b/2a
потом возьмем произвольные точки х и симметричные им, и найдем в них значение функции;
график пересекает ось абсцисс в точках х=1/5, х=2
Слайд 31Графический способ решения квадратных уравнений
Перепишем исходное уравнение как
5х2 =11х-2, и
y=5х2, y=11х-2, они пересекутся в точках с абсциссами х=1/5, х=2
Слайд 32О проекте
Данный проект был создан учениками девятого класса для восьмиклассников в
Слайд 33Список использованной литературы
Большая советская энциклопедия
Мордкович А. Г. Алгебра – 8
Макарычев Ю.
Алимов Ш. А. Алгебра-8
Слайд 34Теорема Виета для корней квадратного уравнения
* * *
По праву
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты корни — и дробь уж готова:
В числителе с, в знаменателе а,
А сумма корней тоже дроби равна.
Хоть с минусом дробь эта, что за беда —
В числителе b, в знаменателе а.
Слайд 35Задания для самоконтроля
Являются ли следующие уравнения квадратными?
-х2=0
7х2-13=0
1-15х=0
0х2-14х+5=0
-5х+12х2=0
Ответы.
х2-4х+3=0
5х2+3х-8=0
5х2+14х-3=0
35х2+2х-1=0
25=26х-х2
3х2-8х+5=0
у2=4у+96
у2-10у+25=0
Ответы.
Слайд 36Ответы.
Да
Да
Нет
Нет
Да
х1=1; х2=3
х1=-1,6; х2=1
х1=-3; х2=0,2
х1=-0,2; х2=1/7
х1=1; х2=25
х1=1; х2=5/3
у1=-8; у2=12
у=5
Слайд 41Неполные квадратные уравнения
Если в квадратном уравнение ах2+bх+с=0 хотя бы один
Слайд 43Неполное квадратное уравнение при b=0
Уравнение примет вид ах2+с=0 и мы решаем
ах2 =-с
х2 =-с/а
Пример:
Решить -3x2+15=0
-3x2=-15
x2=-15/(-3)
x2=5
Слайд 44Неполное квадратное уравнение при c=0
Уравнение примет вид ах2+bx=0 и мы решаем
x(аx+b) =0
x=0 или ax+b=0
ax=-b
x=-b/a
Пример:
Решить 5x2-15x=0
5x(x-3)=0
x=0 или x-3=0
x=3
Слайд 45Неполное квадратное уравнение при b=0, c=0
Уравнение примет вид ах2=0 и мы
ах2 =0
х2 =0
x=0
Пример:
Решить -81x2=0
x2=0
x=0
Слайд 46Решение неполных квадратных уравнений
Решить 4x2-9=0
9/4
Решить 5x2=0
0 5 1/5
Решить 4x2-3x=0
±3/2 0; ¾ 0; 4/3
А
А
А
В
В
В
С
С
С
Слайд 55Презентацию создали:
Ученики 9 «А» класса 588 школы
ЦАО:
Нгуен Зунг
при поддержки учителя
математики и информатики
Белецкой Наталии Ивановны.
Москва, 2007 г.