- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
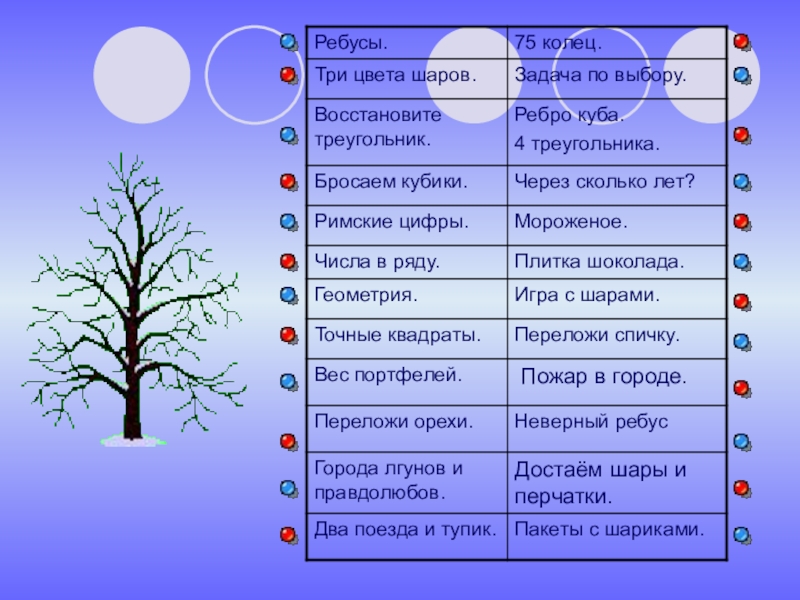
Презентация, доклад на тему Ребусы и логические задачи по математике для учащихся 5-х классов
Содержание
- 1. Ребусы и логические задачи по математике для учащихся 5-х классов
- 2. Слайд 2
- 3. Ребусы.Задача №3.Сколько раз встретится цифра 5 в
- 4. В трёх ящиках лежат белые, синие и
- 5. Выясните, по какому правилу расположены числа в
- 6. Бросаем два кубика.Бросают два игральных кубика. На
- 7. В римской нумерации записано
- 8. Восстановите треугольник.Даны три прямые, которые пересекаются в
- 9. Геометрия.
- 10. Найдите наибольшее натуральное число, любые две последовательные
- 11. Вес портфелей.Митя и Витя взвесили свои портфели.
- 12. Переложи орехи.В трёх кучках 22, 14 и
- 13. Города лгунов и правдолюбов.Два города А и
- 14. Задача по выбору.В классе 36 учеников. Каждому
- 15. 75 колец.Из 75 одинаковых по виду колец
- 16. Ребро куба. Четыре треугольника.Имеется куб, который
- 17. Через сколько лет?Решение: Сейчас детям вместе 29
- 18. Мороженое.Решение: У одного ученика был либо один
- 19. Плитка шоколада.Плитка шоколада прямоугольной формы состоит из
- 20. Игра с шарами.В первом ящике 15 синих
- 21. Переложи спичку.Из спичек выложено равенство: XIV
- 22. Неверный ребус.
- 23. Достаём шары и перчатки.Ответ: в первом случае
- 24. Два поезда и тупик.На рисунке показан железнодорожный
- 25. Пожар в городе.Жители города А говорят только
- 26. Пакеты с шариками. В четырёх пакетах лежат
Слайд 1для учащихся 5 класса.
Составитель: Руднева Н.В.,
учитель математики.
Внеклассные
задачи
МБОУ Лицей №1
Слайд 3
Ребусы.
Задача №3.
Сколько раз встретится цифра 5 в ряду чисел: 1,2.3,4,…,98,99?
Вместо звёздочки поставьте цифры, если известно, что каждое из чисел не меняет своего значения, если прочитать его справа налево:
* * + * * * = * * * *
Ответ: 22 + 979 = 1001.
Ребус №2.
Замените звёздочки цифрами так, чтобы получилось верное равенство:
* * * * + * * * * = * 9997.
Ответ:
9998+9999=19997
или 9999+9998=19997.
в числе единиц –
Решение: в числе десятков
Ответ: 20 раз.
-10 раз,
10 раз.
Всего 20 раз.
Слайд 4В трёх ящиках лежат белые, синие и красные шары. В ящике
Ответ: Синий и красный.
Решение: Можно заметить, что в каждом ящике лежит шар, цвет которого указан на коробке первым, а цвет второго шара на коробке указан неверно.
Три цвета шаров.
Слайд 5Выясните, по какому правилу расположены числа в ряду:
186, 345, *
Найдите третий член ряда.
Решение:
Первые цифры указанных чисел составляют последовательность
Числа в ряду.
составляют убывающую последовательность:8,4,2,1
(каждое последующее число в два раза меньше предыдущего).
также составляют убывающую последовательность:
6,5,4,3.
Ответ: 524.
первых четырёх нечётных чисел:1,3,5,7.
Вторые цифры
Третьи цифры
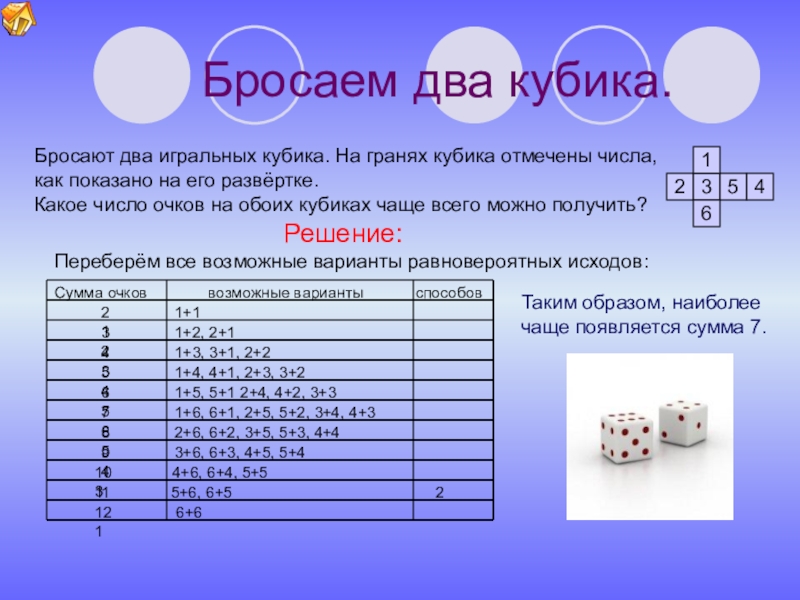
Слайд 6Бросаем два кубика.
Бросают два игральных кубика. На гранях кубика отмечены числа,
как показано на его развёртке.
Какое число очков на обоих кубиках чаще всего можно получить?
2
3
5
4
1
6
Решение:
Переберём все возможные варианты равновероятных исходов:
Сумма очков возможные варианты способов
2 1+1 1
3 1+2, 2+1 2
4 1+3, 3+1, 2+2 3
5 1+4, 4+1, 2+3, 3+2 4
6 1+5, 5+1 2+4, 4+2, 3+3 5
7 1+6, 6+1, 2+5, 5+2, 3+4, 4+3 6
8 2+6, 6+2, 3+5, 5+3, 4+4 5
9 3+6, 6+3, 4+5, 5+4 4
10 4+6, 6+4, 5+5 3
11 5+6, 6+5 2
12 6+6 1
Таким образом, наиболее
чаще появляется сумма 7.
Слайд 7 В римской нумерации записано какое-то число. К нему
Римские цифры.
Ответ: число V (5).
Получим
в результате преобразования
Х (10).
Слайд 8Восстановите треугольник.
Даны три прямые, которые пересекаются в одной точке.
Эти прямые являются
Восстановите треугольник, если задана вершина А треугольника.
Решение:
1. Отразим точку А симметрично
относительно прямых, которые
не содержат точку А.
2. Проведём через
точки А1 и А2 прямую.
А1
А2
3. Точки пересечения В и С этой прямой с двумя
биссектрисами, не проходящими через А,
будут вершинами искомого треугольника.
В
С
А
Обе точки лежат на стороне
треугольника,
противоположной вершине А.
Получим точки А1 и А2.
Слайд 9Геометрия.
Задача 1.
Длины всех
треугольника
выражаются целым числом
дециметров.
Одна сторона 3 дм,
другая 1 дм.
Каков периметр треугольника?
Какой геометрический принцип лежит в разбивке букв по следующим группам:
I -А, Д, М, П, Т, Ф, Ш;
II -В, Е, З, К, С, Э, Ю;
III - О, Ж, Х, Н,
IV -Б, Г, Л, И, Р, У, П, Ч, Ь, Ъ, Ы, Я?
Решение: Третья сторона треугольника
должна быть больше разности
двух других сторон(чем3-1=2)
и меньше суммы этих
сторон(чем 3+1=4).
Это натуральное
число 3.
буквы симметричны относительно вертикальной оси;
буквы симметричны относительно горизонтальной оси;
буквы симметричны относительно обеих осей;
буквы не имеют осей симметрии.
Задача 2.
Периметр треугольника
равен 7 дм.
Слайд 10Найдите наибольшее натуральное число, любые две последовательные цифры которого образуют точный
Ответ: 81 649.
Точные квадраты.
Покажите, что это число наибольшее.
Начнём с наибольшего квадрата числа 9, т.е. 81,
Решение: 8 1
6
4
9
с 1-цы начинается квадрат 4, т.е. 16,
с 6-ки получим квадрат числа 8, т.е. 64,
продолжение должно быть 49.
Это число наибольшее, т.к. на 9 нет квадрата числа, состоящего из двух цифр.
Слайд 11Вес портфелей.
Митя и Витя взвесили свои портфели. Весы показали 3 кг
-Разве два плюс три равно шести?- воскликнул Витя.
Решение:
Так как пять меньше шести, то весы обманывают в меньшую сторону.
-У весов сдвинута шкала,-
догадался Митя.
-Они показывают вес, который
отличается на некоторую
определённую величину от истинного.
Сколько весили портфели на самом деле?
Итак, вес 1-го портфеля 3+1=4 кг, 2-го 2+1=3 кг. Истинный вес портфелей
4+3=7 кг, на весах 7-1=6 кг.
Разница в 1 кг даёт ошибку в 1 кг.
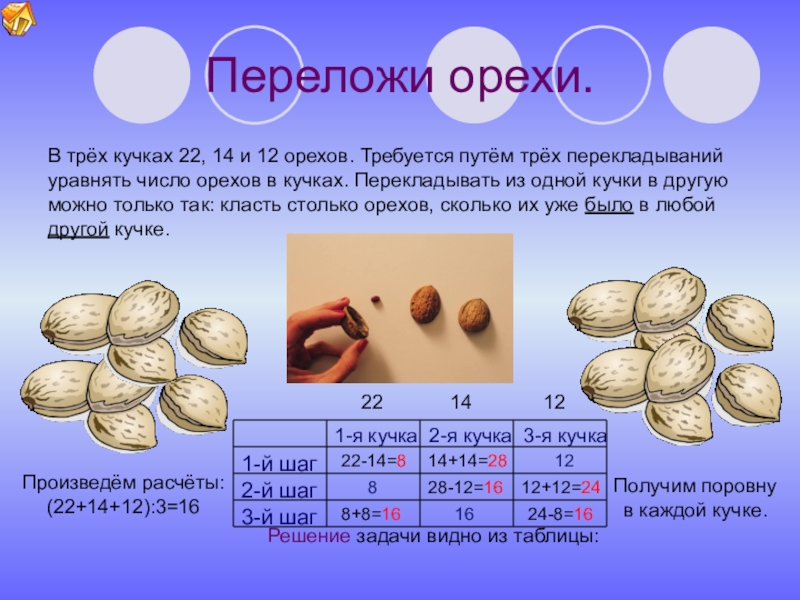
Слайд 12Переложи орехи.
В трёх кучках 22, 14 и 12 орехов. Требуется путём
22-14=8
14+14=28
12
8
28-12=16
12+12=24
8+8=16
16
24-8=16
1-й шаг
2-й шаг
3-й шаг
1-я кучка 2-я кучка 3-я кучка
Решение задачи видно из таблицы:
22 14 12
Произведём расчёты:
(22+14+12):3=16
Получим поровну
в каждой кучке.
Слайд 13Города лгунов и правдолюбов.
Два города А и В расположены рядом. Жители
Решение: следует задать вопрос: «Вы живёте в этом городе?»
Какой вопрос следует задать жителю, которого вы встречаете в одном из городов(вы не знаете, в каком), чтобы по его ответу «да» или «нет» можно было сразу же определить, в каком городе вы находитесь?
Ответ «да»-независимо от того, кто отвечает,-
означает, что вы находитесь в городе А.
Ответ «нет» при любых условиях будет означать,
что вы находитесь в городе В.
Слайд 14Задача по выбору.
В классе 36 учеников. Каждому было дано задание решить
Так как ученик решает одну задачу, то должно получиться 36 решений, а задач всего 17 видов,
следовательно, согласно принципу Дирихле, хотя бы одну задачу решали трое.
Доказательство: 36 : 17 =2 (ост 2).
Слайд 1575 колец.
Из 75 одинаковых по виду колец одно несколько отличается от
Решение:
Например, можно разбить все кольца на 3 кучки: 20,20 и 35.
Затем положить 2 кучки по 20 колец на разные чашки весов.
Если вес их окажется одинаковым,
то сравнить оставшиеся
35 колец с 35 кольцами из 40 одинаковых, которые лежат на весах.
Если же одна из кучек (по 20 колец) оказалась легче, то сравнить её
с 20 из 35 одинаковых, которые не были использованы во взвешивании.
Слайд 16Ребро куба.
Четыре треугольника.
Имеется куб, который содержит столько же кубических сантиметров,
всей его поверхности. Какая длина ребра у этого куба?
Как из шести спичек, не ломая их,
сложить четыре треугольника,
каждая сторона которых
равна одной спичке?
Решение:
Из шести спичек составляется правильная треугольная пирамида.
Ответ: длина ребра 6.
Слайд 17Через сколько лет?
Решение: Сейчас детям вместе 29 лет. Если пройдёт Х
Отцу 41 год, старшему сыну 13 лет, дочери 10 лет, а младшему сыну 6 лет.
Через сколько лет отцу будет столько лет, сколько его детям, вместе взятым?
Ответ: через шесть лет.
Решая уравнение 41+Х=29+3Х, получим Х=6.
Слайд 18Мороженое.
Решение: У одного ученика был либо один рубль,
Два ученика хотели
а у другого 2 рублей. Тогда они сложили свои деньги вместе, и всё равно им
не хватило на покупку даже одной порции. Сколько стоила одна порция
мороженого?
либо не было ни одного.
Поэтому одна порция мороженого стоила
либо 21 рубль,
либо 20 рублей.
Ответ: 20 рублей или 21 рубль.
Слайд 19Плитка шоколада.
Плитка шоколада прямоугольной формы состоит из 5*8 равных долек. Она
разламывается на сорок одинаковых отдельных частей по прямым,
разделяющим дольки. Сколько раз придётся для этого ломать плитку на дольки?
Ответ: 39 раз.
поэтому при любом способе
разломов их будет 39.
Правило:
N –число кусков,
N-1-число разломов.
Решение: т.к. 5*8=40 и
при каждом разломе число кусков
увеличивается на 1,
Слайд 20Игра с шарами.
В первом ящике 15 синих шаров, во втором 12
Решение:
В первом ящике 5 групп по 3 шара, во втором - 6 групп по 2 шара. Первый игрок должен брать шары так, чтобы число групп в обоих ящиках было одинаковым,
т.е. первым ходом он должен взять
одну группу из второго ящика
(2 белых).
Этим ходом он заставит противника
нарушить это равенство.
Отсюда следует, что положение
0 групп в первом ящике
наступит раньше, чем во втором.
Слайд 21Переложи спичку.
Из спичек выложено равенство: XIV – XVI = II
Переместите
Ответ: XIV = XVI - II
Слайд 22Неверный ребус.
Решение
Х 4 0 1
5 1
-------
4 0 1
2 0 0 5
----------
2 0 4 5 1
В математическом кружке составляли числовые ребусы. Один из учеников
Придумал такой ребус: х * 0 * Учитель посмотрел на этот ребус и сказал:
5 1 «Одна из цифр результата неверна.
------ Кроме того, её вообще можно заменить
* * * звёздочкой и расшифровать ребус».
* * 0 *
----------- Расшифруйте этот ребус и выясните,
* * 4 6 * какая цифра неверна.
Решение: Неверная цифра 6.
0
5или0
4
4
20
20
Решение 2:
Х 4 0 0
5 1
-------
4 0 0
2 0 0 0
----------
2 0 4 0 0
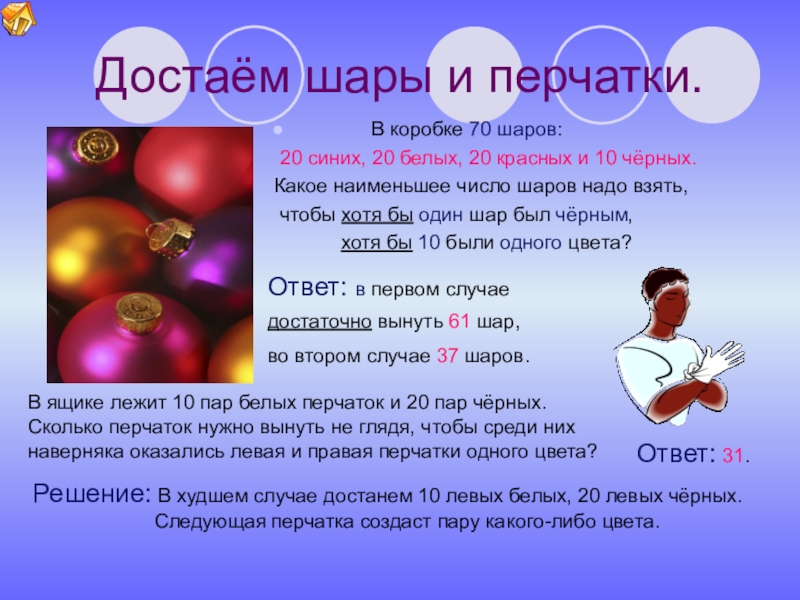
Слайд 23Достаём шары и перчатки.
Ответ: в первом случае
достаточно вынуть 61 шар,
В коробке 70 шаров:
20 синих, 20 белых, 20 красных и 10 чёрных.
Какое наименьшее число шаров надо взять,
чтобы хотя бы один шар был чёрным,
хотя бы 10 были одного цвета?
во втором случае 37 шаров.
В ящике лежит 10 пар белых перчаток и 20 пар чёрных.
Сколько перчаток нужно вынуть не глядя, чтобы среди них
наверняка оказались левая и правая перчатки одного цвета?
Ответ: 31.
Решение: В худшем случае достанем 10 левых белых, 20 левых чёрных.
Следующая перчатка создаст пару какого-либо цвета.
Слайд 24Два поезда и тупик.
На рисунке показан железнодорожный разъезд, на котором находятся
10 вагонов, а в тупике Т помещается только 5 вагонов и один паровоз?
Паровоз А! Проезжай вперёд, но не забудь вернуть чужие вагоны,
загнав их в тупик!
Сначала в тупик Т загоняют пять вагонов,
а оставшиеся вагоны поезда Б вместе с
паровозом проезжают вперёд.
Затем поезд А проходит также вперёд и ,захватывая из тупика Т
пять находящихся там вагонов, движется в первоначальное положение.
Такие же манёвры проводят с остальными пятью вагонами и паровозом Б.
Решение:
Слайд 25Пожар в городе.
Жители города А говорят только правду, жители города В
а жители города С –попеременно правду и ложь (т.е. из двух высказанных
ими утверждений одно истинно, а другое ложно).
Ответ: в город А.
В пожарную часть сообщили по телефону:
«У нас пожар, скорее приезжайте!»
«Где?»-спросил дежурный по части.
«В городе С»,-ответили ему.
В какой город должна приехать машина?
Решение:
звонили не из города А (неверно 2-е утверждение),
и не из города С (д.б. неверно 2-е утверждение, но оно верно).
Значит, звонили из города В. Неверное «У нас» означает А или С,
неверное «В городе С» оставляет только А.
Слайд 26Пакеты с шариками.
В четырёх пакетах лежат по 5 шариков, причём
пакетах каждый шарик весит по 10 г, а в оставшемся
пакете по 9 г.
Как одним взвешиванием
на точных весах с гирями
определить, в каком
пакете более
лёгкие шарики?
Решение:
Надо взять из первого пакета -1 шарик,
из второго - 2, из третьего - 3 и из четвёртого
4 шарика.
Сколько граммов не будет хватать на весах
до 100 г, таков и номер интересующего нас
пакета.