- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Реализация новых ФГОС по математике в основной и старшей школе.
Содержание
- 1. Реализация новых ФГОС по математике в основной и старшей школе.
- 2. Новые ФГОС
- 3. Как обучать? С помощью чего учить? Как проверить достижение новых образовательных результатов?
- 4. Слайд 4
- 5. Как обучать?
- 6. Дидактические принципы
- 7. С помощью чего учить?
- 8. Урок
- 9. Урок
- 10. Урок
- 11. Пример 1: Урок по теме «Сумма углов
- 12. Пример 2: Исследовательская работа на уроке по
- 13. Как проверить достижение новых
- 14. УУД
- 15. Уровень сформированности способностей к дифференцированию, конкретного или
- 16. http://www.sch2000.ru/
Новые ФГОС
Слайд 3Как обучать?
С помощью чего учить?
Как проверить достижение новых образовательных
результатов?
Слайд 11Пример 1: Урок по теме «Сумма углов треугольника» – геометрия 7
класс УМК А.В. Погорелова или Л.С.Атанасяна.
Проблемная ситуация (задание невыполнимое вообще): Постройте треугольник с углами 9000, 12000, 6000.
Побуждающий диалог.
Учитель: – Вы можете начертить такой треугольник? (Побуждение к осознанию противоречия.)
Ученик: – Нет, не получается! (осознание затруднения.)
Учитель: – Какой же вопрос возникает? (Побуждение к формулировке проблемы.)
Ученик: – Почему не строится треугольник? (Проблема как вопрос, не совпадающий с темой урока.)
Формулировка учебной проблемы.
Диалог, побуждающий к выдвижению и проверке гипотезы.
– Начертите треугольник.
– Измерьте его углы транспортиром.
– Найдите сумму углов.
– Какие результаты у вас получились?
– К какому круглому числу приближаются ваши результаты?
– Что же можно предположить о сумме углов треугольника?
– Сверим вывод с учебником.
– А почему у вас получились неточные результаты?
Проблемная ситуация (задание невыполнимое вообще): Постройте треугольник с углами 9000, 12000, 6000.
Побуждающий диалог.
Учитель: – Вы можете начертить такой треугольник? (Побуждение к осознанию противоречия.)
Ученик: – Нет, не получается! (осознание затруднения.)
Учитель: – Какой же вопрос возникает? (Побуждение к формулировке проблемы.)
Ученик: – Почему не строится треугольник? (Проблема как вопрос, не совпадающий с темой урока.)
Формулировка учебной проблемы.
Диалог, побуждающий к выдвижению и проверке гипотезы.
– Начертите треугольник.
– Измерьте его углы транспортиром.
– Найдите сумму углов.
– Какие результаты у вас получились?
– К какому круглому числу приближаются ваши результаты?
– Что же можно предположить о сумме углов треугольника?
– Сверим вывод с учебником.
– А почему у вас получились неточные результаты?
Слайд 12Пример 2: Исследовательская работа на уроке по теме «Признаки делимости на
3 и 9» – математика 5-6 УМК Л.Г.Петерсон или Н.Я. Виленкина или Г.В.Дорофеева и И.Ф. Шарыгина.
1. Представьте число 8535 в виде суммы разрядных слагаемых.
2. Каждое круглое число представьте в виде суммы двух слагаемых, одно из которых равно 1 (например: 100 = 99 + 1).
3. Раскройте скобки, применив распределительный закон ( a·(b + c) = a·c + b·c ).
4. Пользуясь законами сложения, упростите полученное выражение, заключив в скобки слагаемые, не входящие в произведения. Выполните сложение в скобках.
5. Будет ли данное выражение делится на 3, согласно свойствам делимости суммы и произведения?
6. Подумайте, от делимости на 3 какого слагаемого будет зависеть делимость всего выражения?
7. Как получилось это слагаемое? Что это за цифры?
8. Попробуйте сделать вывод о том, когда число делится на 3? Сформулируйте правило.
9. Проверьте свой вывод по учебнику.
1. Представьте число 8535 в виде суммы разрядных слагаемых.
2. Каждое круглое число представьте в виде суммы двух слагаемых, одно из которых равно 1 (например: 100 = 99 + 1).
3. Раскройте скобки, применив распределительный закон ( a·(b + c) = a·c + b·c ).
4. Пользуясь законами сложения, упростите полученное выражение, заключив в скобки слагаемые, не входящие в произведения. Выполните сложение в скобках.
5. Будет ли данное выражение делится на 3, согласно свойствам делимости суммы и произведения?
6. Подумайте, от делимости на 3 какого слагаемого будет зависеть делимость всего выражения?
7. Как получилось это слагаемое? Что это за цифры?
8. Попробуйте сделать вывод о том, когда число делится на 3? Сформулируйте правило.
9. Проверьте свой вывод по учебнику.
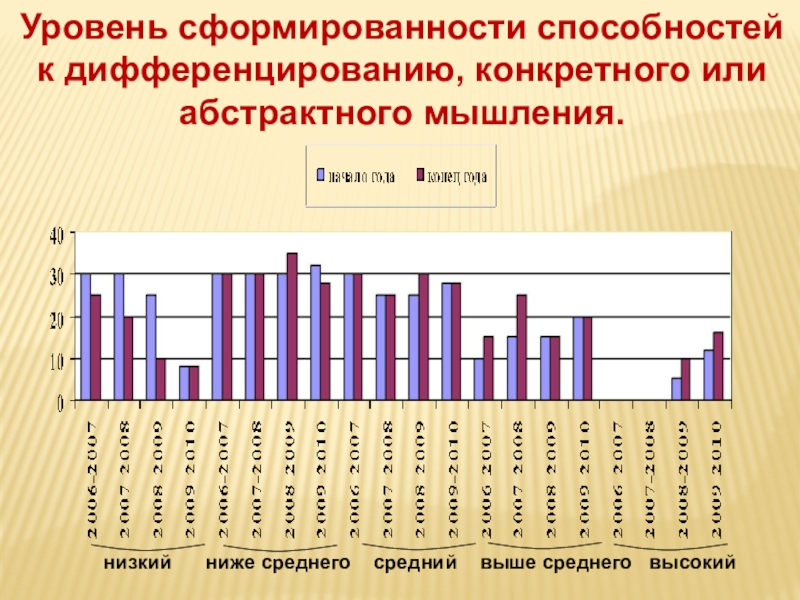
Слайд 15Уровень сформированности способностей к дифференцированию, конкретного или абстрактного мышления.
низкий ниже среднего средний выше среднего высокий