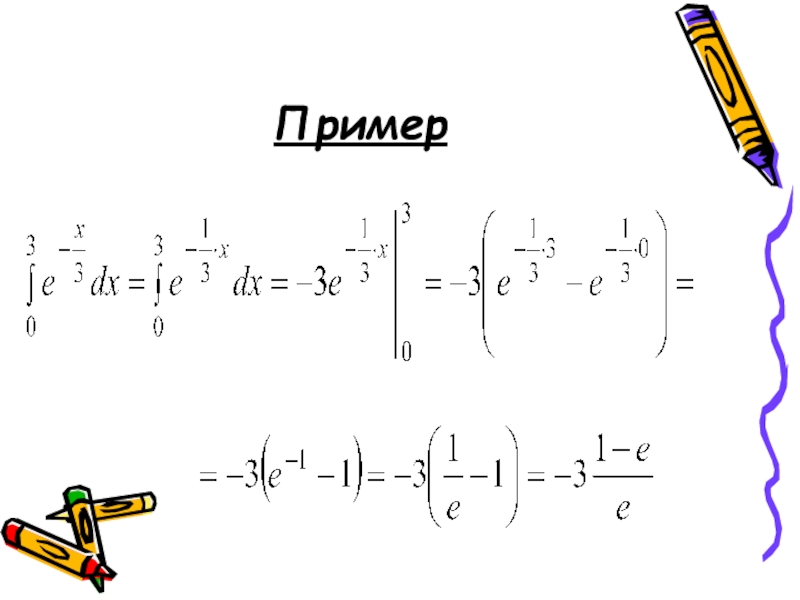- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Разработка урока на тему Интеграл
Содержание
- 1. Разработка урока на тему Интеграл
- 2. Эпиграф: «Кто с детских лет занимается
- 3. Тема: Интеграл.Цели урока: 1) обобщить и систематизировать
- 4. Определенный интеграл
- 5. Определенный интеграл
- 6. Определенный интеграл
- 7. Теорема о существовании определенного интеграла
- 8. Свойства определенного интеграла
- 9. Свойства определенного интеграла
- 10. Вычисление определенного интеграла
- 11. Пример
- 12. Вычисление интеграла
- 13. Верны ли равенства: а)
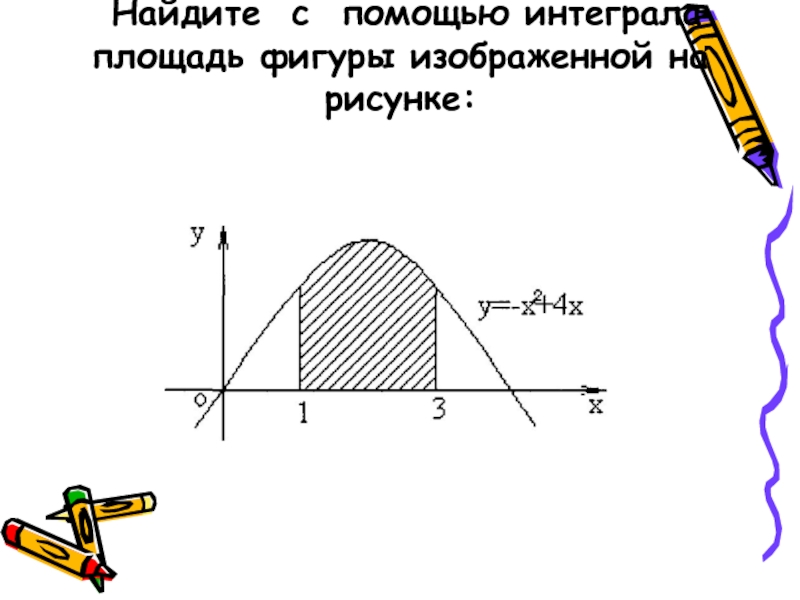
- 14. Найдите с помощью интеграла площадь фигуры изображенной на рисунке:
- 15. Вычислите интеграл:1)
- 16. Вычисление площадейПлощадь фигуры в декартовых координатах.
- 17. Вычисление площадейВ случае параметрического задания кривой, площадь
- 18. ПримерыВычислить площадь фигуры, ограниченной линиями
- 19. Продолжение
- 20. неопределенный интеграл
- 21. Неопределенный интеграл, его свойства и вычисление
- 22. Первообразная и неопределенный интегралОпределение. Функция F(x) называется
- 23. Первообразная и неопределенный интегралОчевидно, если F(x) -
- 24. Первообразная и неопределенный интегралОпределение. Совокупность всех первообразных
- 25. Первообразная и неопределенный интегралЕсли - некоторая первообразная
- 26. Свойства интеграла, вытекающие из определения Производная неопределенного
- 27. Свойства интеграла, вытекающие из определения Неопределенный
- 28. Свойства интегралаСформулируем далее следующие свойства неопределенного интеграла:4.Если
- 29. Свойства дифференциаловПри интегрировании удобно пользоваться свойствами:
Эпиграф: «Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели»
Слайд 2Эпиграф:
«Кто с детских лет занимается математикой, тот развивает внимание,
тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели»
(А.Маркушевич)
(А.Маркушевич)
Слайд 3Тема: Интеграл.
Цели урока:
1) обобщить и систематизировать знания по данной теме;
2)
развить умение применять знания на практике;
3) формировать чувство самоутверждения, самоанализа, самооценки, взаимооценки.
3) формировать чувство самоутверждения, самоанализа, самооценки, взаимооценки.
Слайд 17Вычисление площадей
В случае параметрического задания
кривой, площадь фигуры, ограниченной
прямыми
, осью Ох и кривой
вычисляют по
формуле
где пределы интегрирования определяют из
уравнений .
вычисляют по
формуле
где пределы интегрирования определяют из
уравнений .
Слайд 22Первообразная и неопределенный интеграл
Определение. Функция F(x) называется первообразной функции f(x) ,
определенной на некотором промежутке, если F’(x)=f(x) для каждого x из этого промежутка.
Слайд 23Первообразная и неопределенный интеграл
Очевидно, если F(x) - первообразная функции f(x) ,
то , F(x)+C где C - некоторая постоянная, также является первообразной функции f(x).
Если F(x) есть какая-либо первообразная функции f(x) , то всякая функция вида Ф(x)=F(x)+C также является первообразной функции f(x) и всякая первообразная представима в таком виде.
Если F(x) есть какая-либо первообразная функции f(x) , то всякая функция вида Ф(x)=F(x)+C также является первообразной функции f(x) и всякая первообразная представима в таком виде.
Слайд 24Первообразная и неопределенный интеграл
Определение. Совокупность всех первообразных функции f(x), определенных на
некотором промежутке, называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается .
Слайд 25Первообразная и неопределенный интеграл
Если
- некоторая первообразная функции
, то пишут
, хотя правильнее бы писать
.
Мы по устоявшейся традиции будем писать
.
Тем самым один и тот же символ
будет обозначать как всю совокупность первообразных функции
, так и любой элемент этого множества.
Слайд 26Свойства интеграла, вытекающие из определения
Производная неопределенного интеграла равна подынтегральной функции,
а его дифференциал- подынтегральному выражению. Действительно:
Слайд 27Свойства интеграла, вытекающие из определения
Неопределенный интеграл от дифференциала непрерывно
дифференцируемой функции равен самой этой функции с точностью до постоянной:
3.
3.
так как F(x) является первообразной для F’(x)
Слайд 28Свойства интеграла
Сформулируем далее следующие свойства неопределенного интеграла:
4.Если функции
и имеют первообразные, то функция также имеет первообразную, причем ;
5.;
6.;
7..
5.;
6.;
7..