- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Путешествие в страну Геометрических фигур
Содержание
- 1. Путешествие в страну Геометрических фигур
- 2. «Учиться можно только весело. Чтобы переваривать
- 3. СодержаниеОпределение угла. Развернутый угол.Сравнение углов наложением.Измерение углов.Биссектриса
- 4. Урок 1 Определение угла. Развернутый угол.
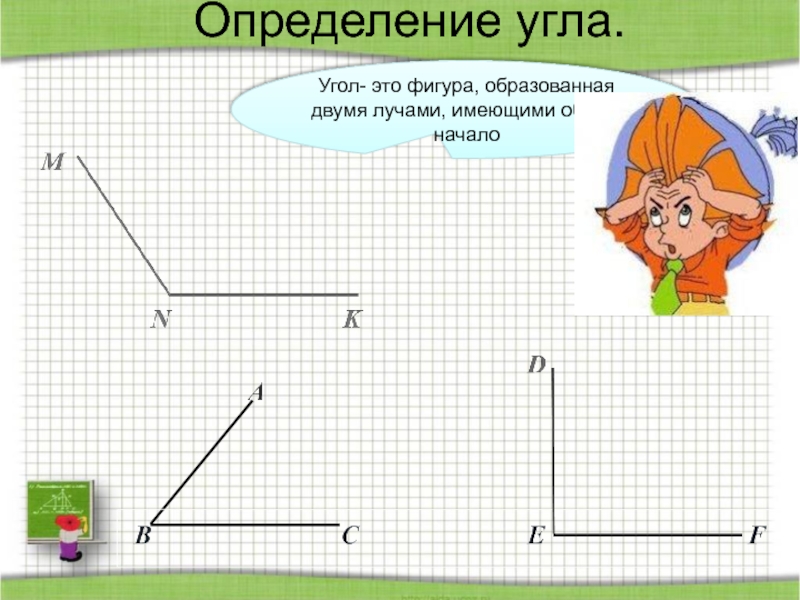
- 5. Определение угла.Угол- это фигура, образованная двумя лучами, имеющими общее начало
- 6. Развернутый угол.Развернутый угол-это угол, образованный дополнительными лучами.O
- 7. Проверь себя.Стороны угла - это два луча
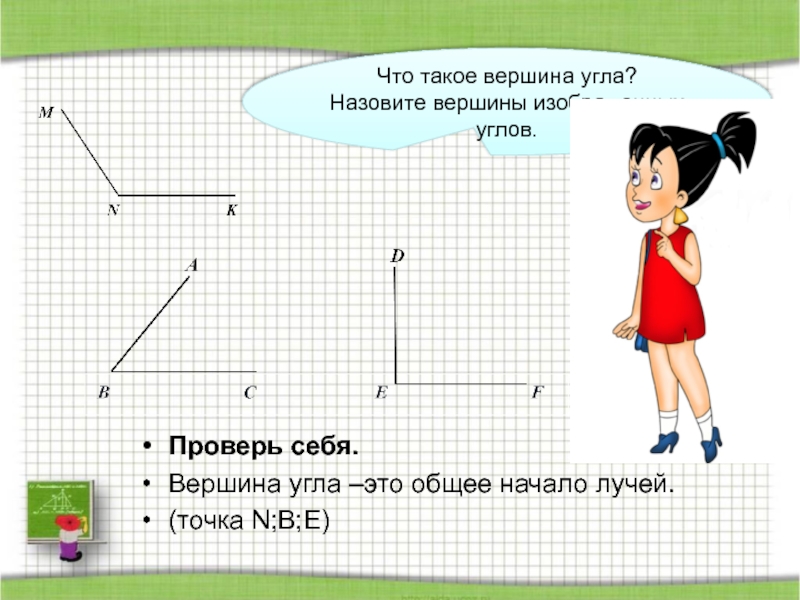
- 8. Что такое вершина угла? Назовите вершины изображенных углов.Проверь себя.Вершина угла –это общее начало лучей.(точка N;B;E)
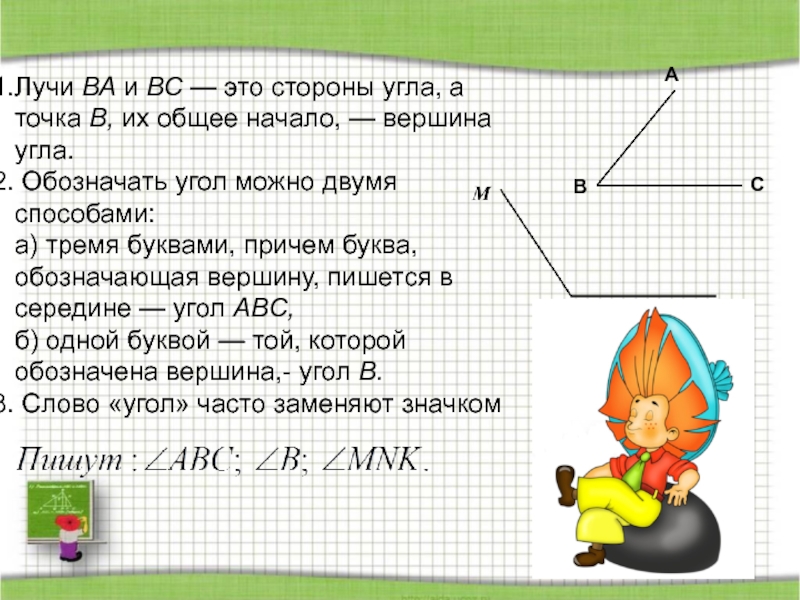
- 9. Лучи ВА и ВС — это стороны
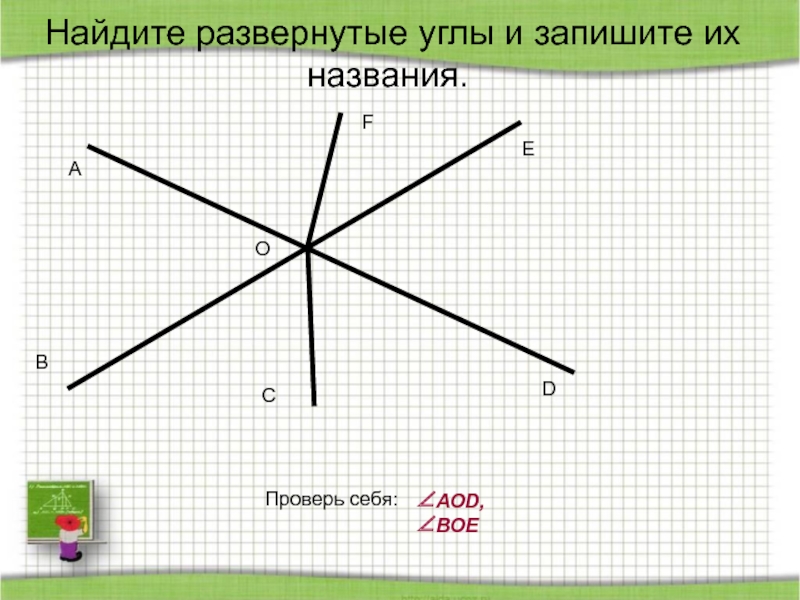
- 10. Найдите развернутые углы и запишите их названия.Проверь себя:∠АОD, ∠ВОE
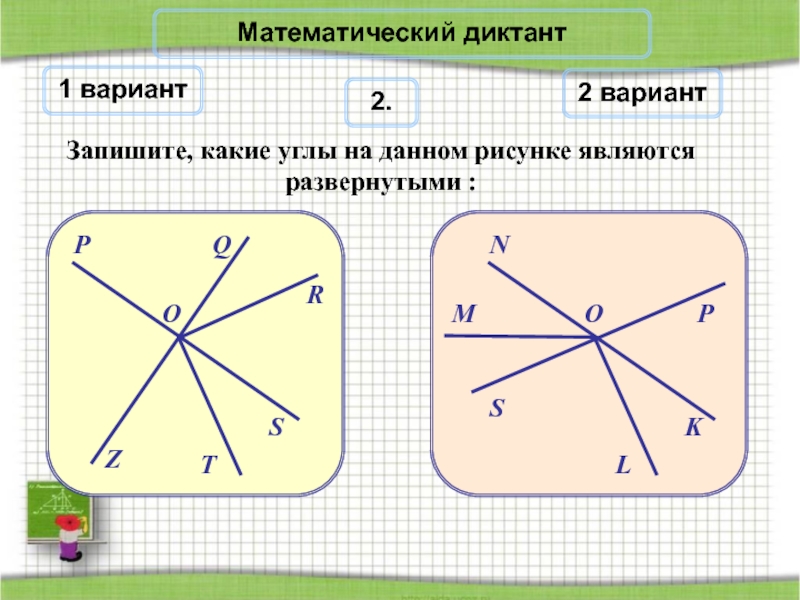
- 11. Математический диктант1 вариант2 вариант1.б) запишите, как обозначена вершина данного угла:в) запишите, как обозначены стороны данного угла:
- 12. Математический диктант1 вариант2 вариант2.
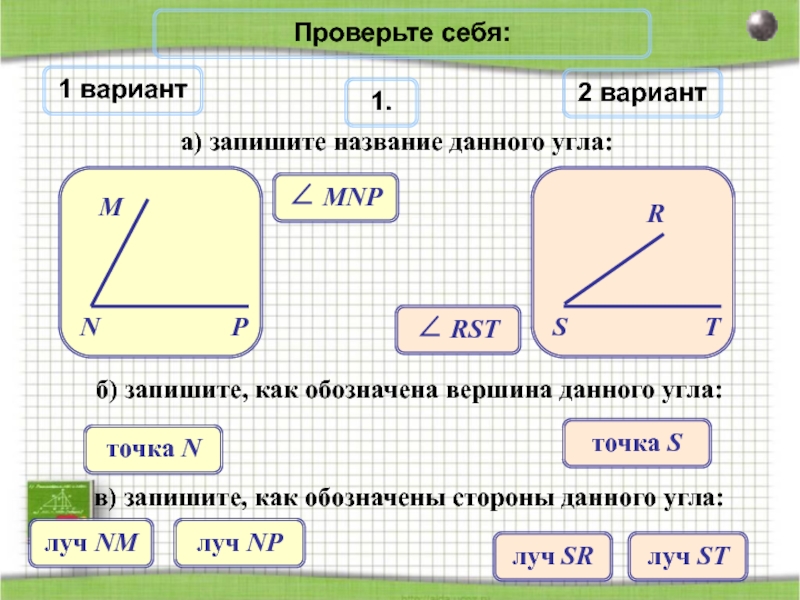
- 13. Проверьте себя:1 вариант2 вариант1.а) запишите название данного
- 14. Урок 2 Сравнение углов наложением.
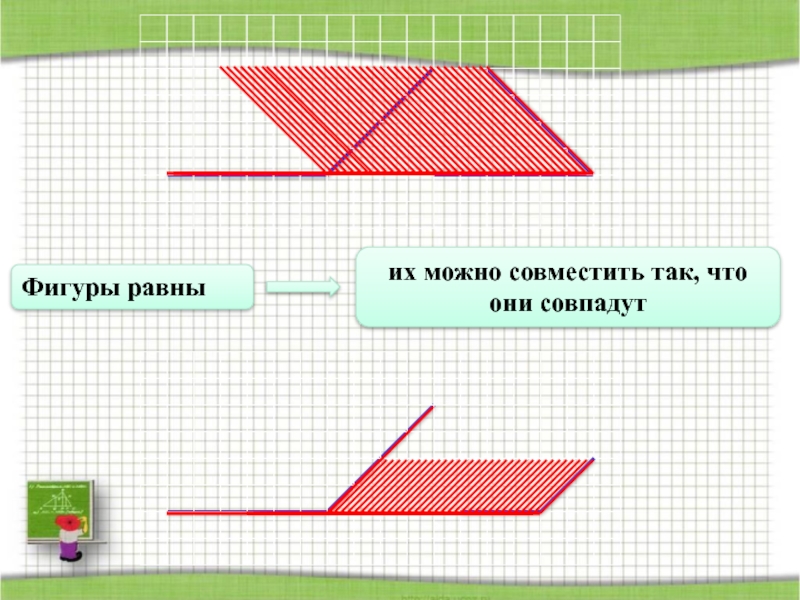
- 15. Вы знаете, что равные фигуры можно совместить
- 16. Фигуры равны их можно совместить так, что они совпадут
- 17. Урок 3 Измерение углов.
- 18. Величину угла измеряют с помощью транспортира
- 19. Виды транспортиров.
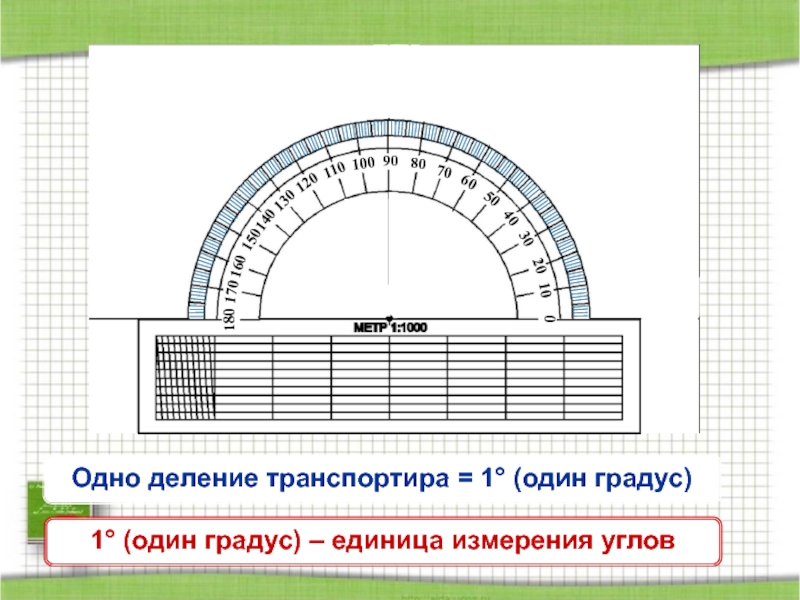
- 20. 0102030405060708090100110120130140160150170180Одно деление транспортира = 1° (один градус)1° (один градус) – единица измерения углов
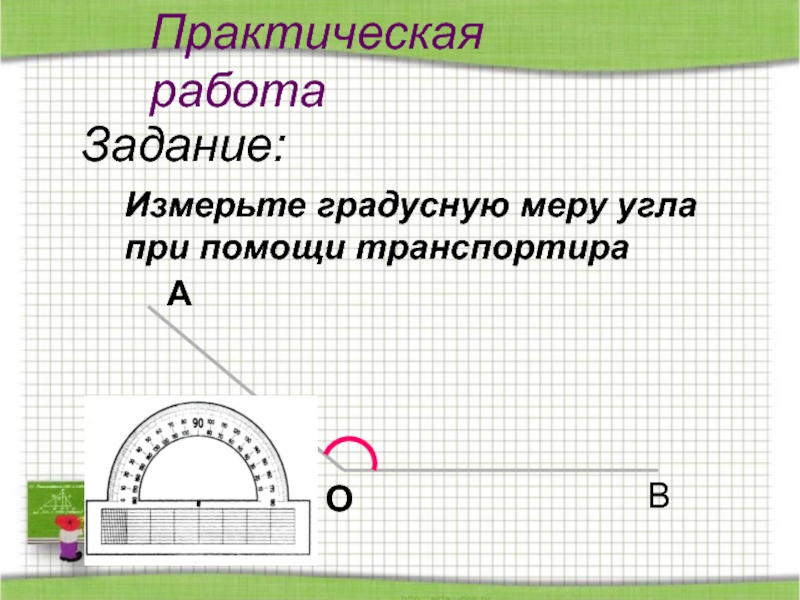
- 21. Практическая работаЗадание:Измерьте градусную меру угла при помощи транспортираАОВ
- 22. Как измерить угол при помощи транспортира?
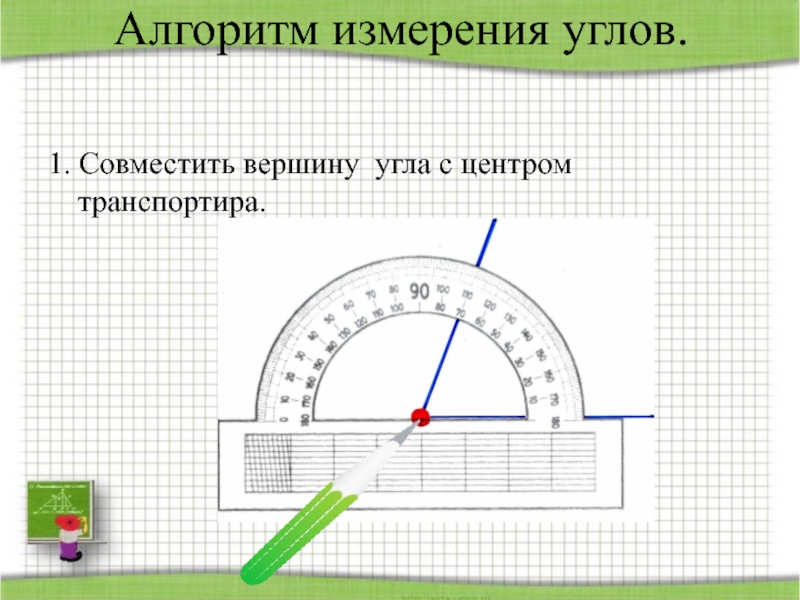
- 23. Алгоритм измерения углов.1. Совместить вершину угла с центром транспортира.
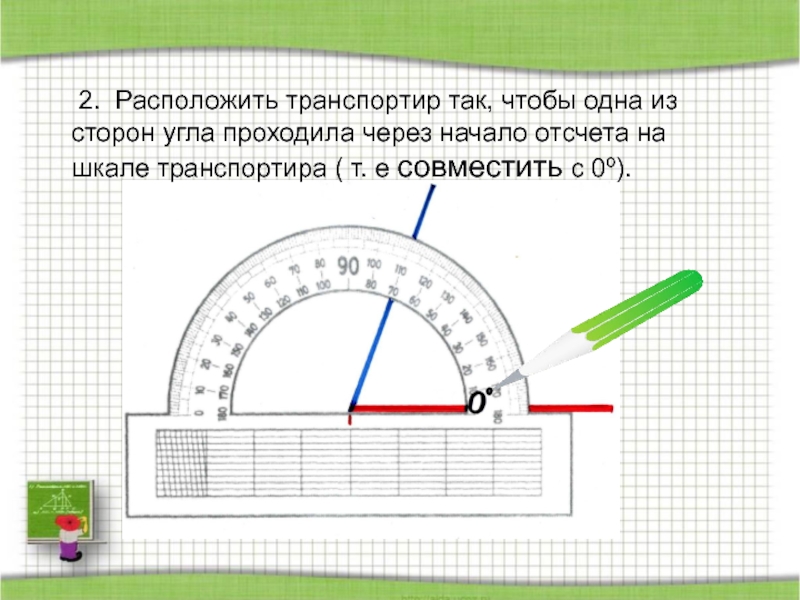
- 24. 2. Расположить транспортир так, чтобы одна
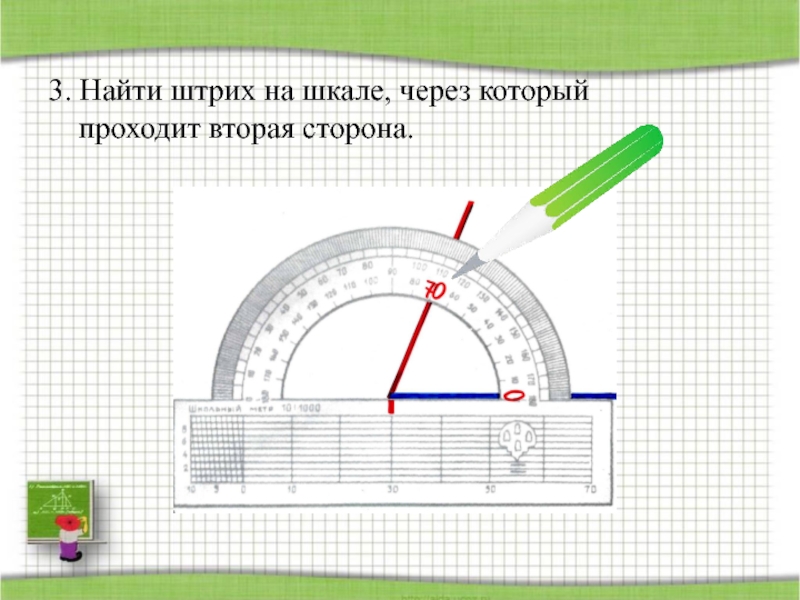
- 25. 3. Найти штрих на шкале, через который проходит вторая сторона.
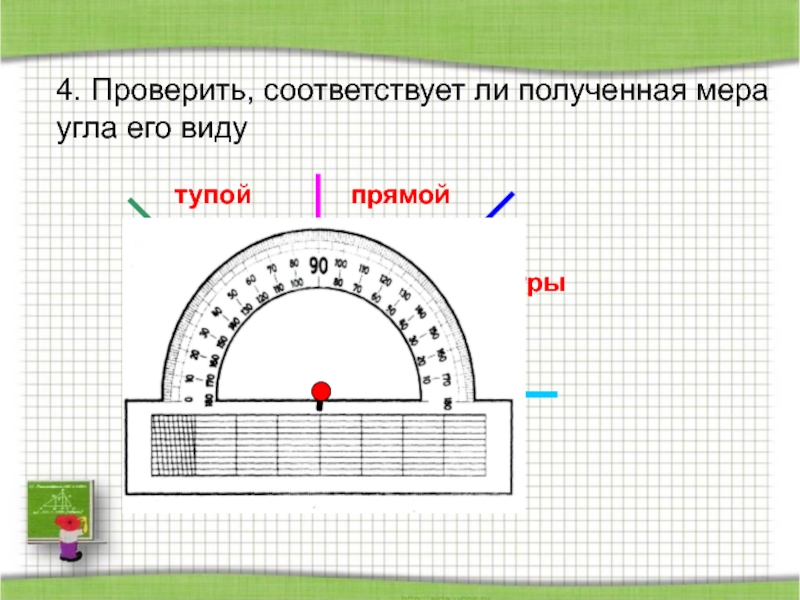
- 26. острыйпрямой тупой 4. Проверить, соответствует ли полученная мера угла его виду
- 27. АCBНа пример.
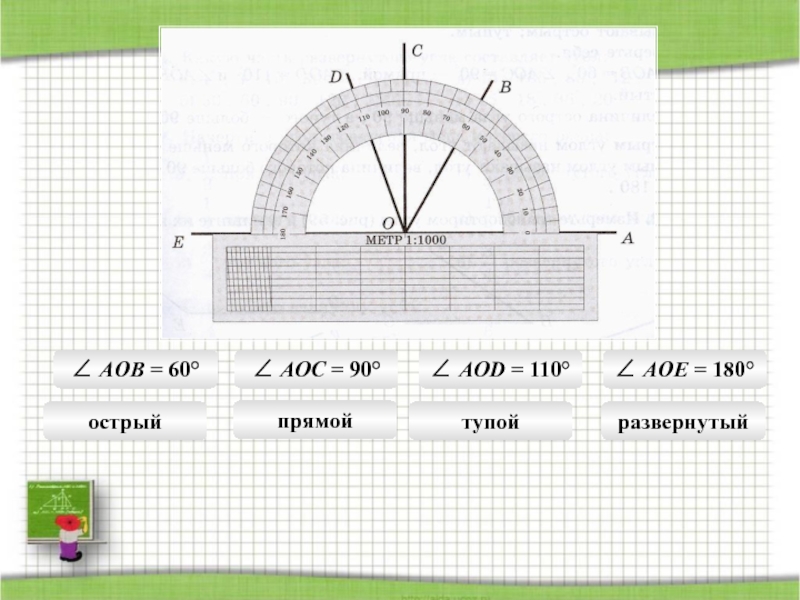
- 28. ∠ AOB = 60°∠ AOC = 90°∠ AOD = 110°∠ AOE = 180°острыйпрямойтупойразвернутый
- 29. Прямым углом называют угол, величина которого равна
- 30. Что нужно для того , чтобы
- 31. Найти градусную меру угла, выполнив вычисления, используя
- 32. Урок 4 Биссектриса угла.
- 33. Этот луч называется биссектрисой угла.Вырежьте из бумаги
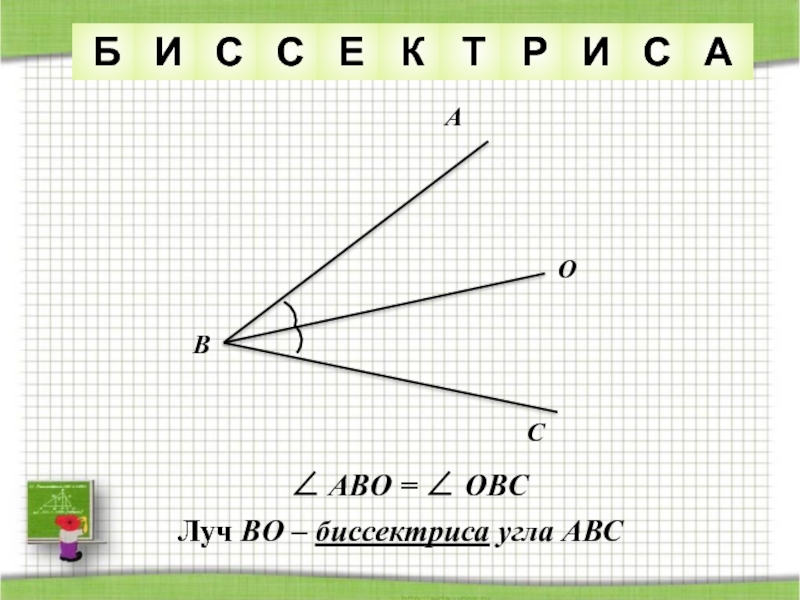
- 34. ACOB∠ ABO = ∠ OBCЛуч BO – биссектриса угла АВС БИССЕКТРИСА
- 35. Биссектриса угла- это луч с началом в
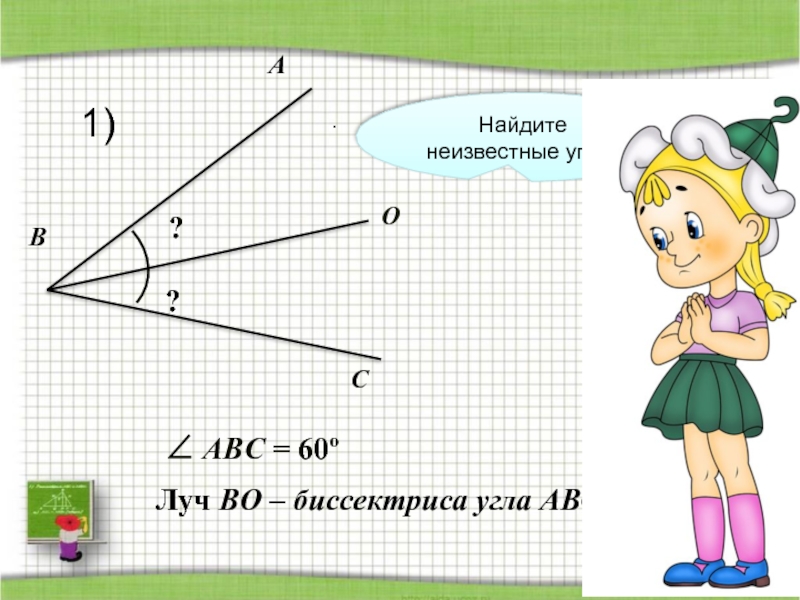
- 36. ACOB?Луч BO – биссектриса угла АВС ?∠ ABС = 60º.Найдите неизвестные углы.1)
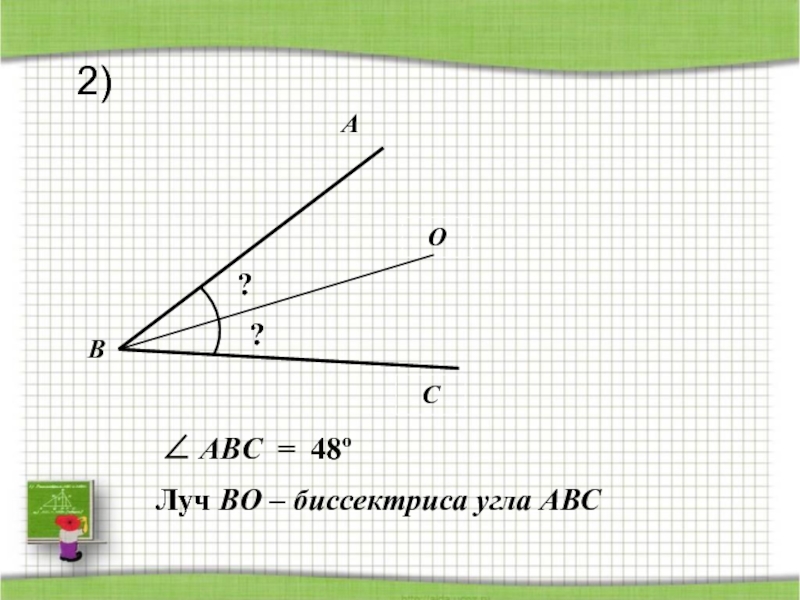
- 37. ACOB?Луч BO – биссектриса угла АВС ?∠ ABС = 48º2)
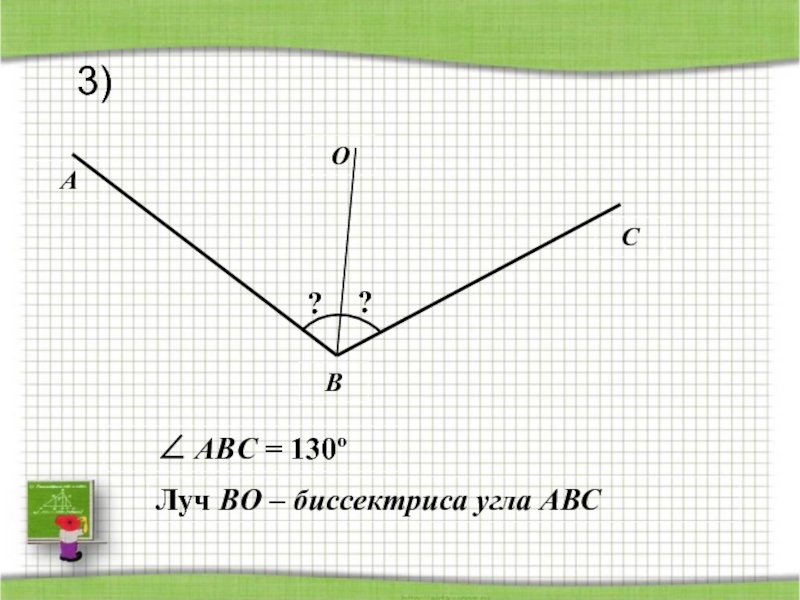
- 38. ACOB?Луч BO – биссектриса угла АВС ?∠ ABС = 130º3)
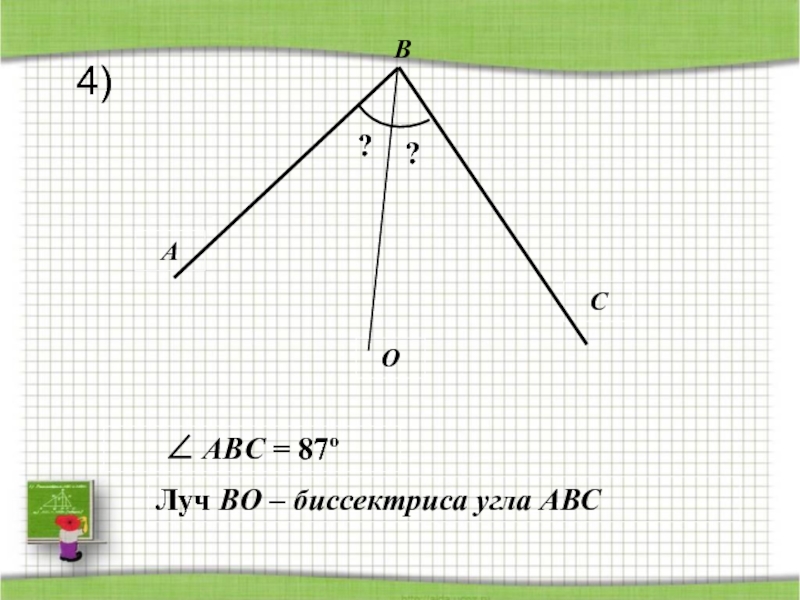
- 39. ACOB?Луч BO – биссектриса угла АВС ?∠ ABС = 87º4)
- 40. Проверь себя.1) 30º2) 24º3) 65º4) 43º5'
- 41. Урок 5 Треугольник.
- 42. BACОстроугольныйВиды треугольников.Остроугольный треугольник – это треугольник у которого все углы острые.
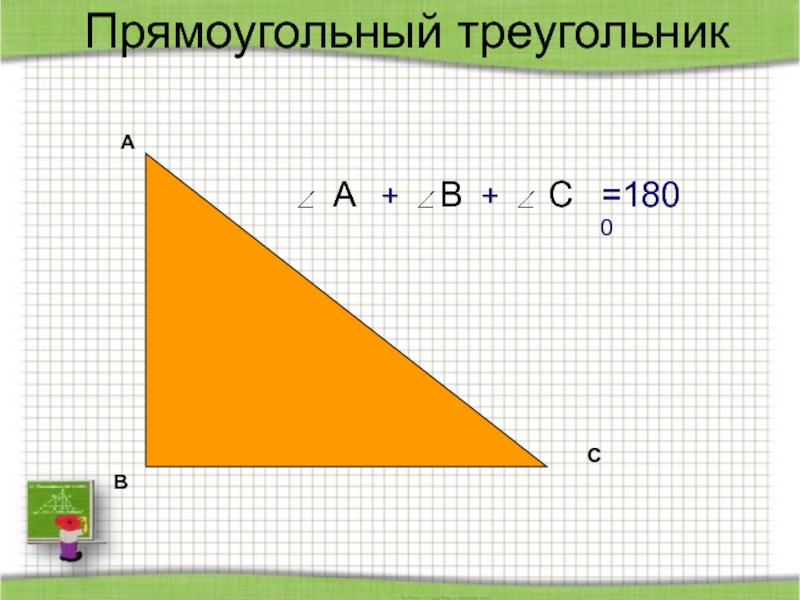
- 43. EFDПрямоугольныйПрямоугольный треугольник – это треугольник, в котором есть прямой угол.
- 44. MKТупоугольныйNТупоугольный треугольник – это треугольник, в котором есть тупой угол.
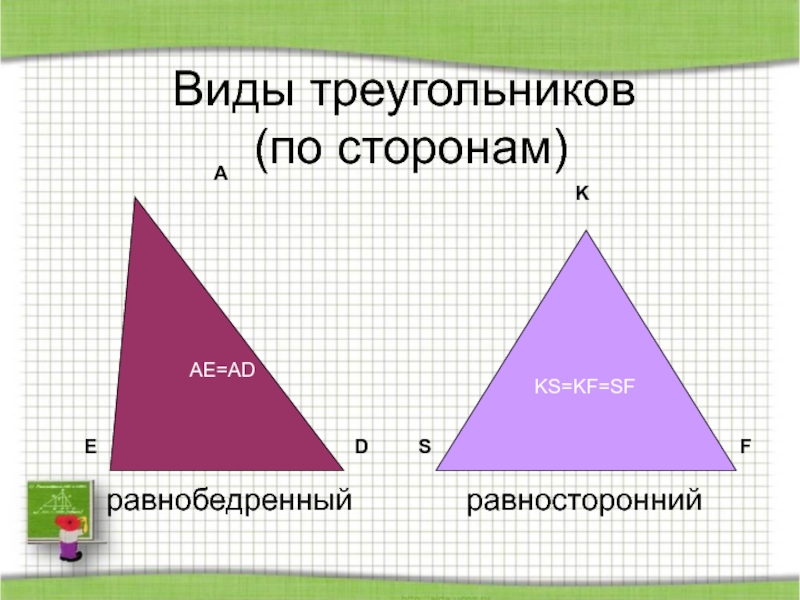
- 45. Виды треугольников (по сторонам)ADEKSFAE=ADKS=KF=SFравнобедренныйравносторонний
- 46. Правило треугольника:«Сумма двух сторон треугольника всегда больше
- 47. Урок 6 Площадь треугольника.
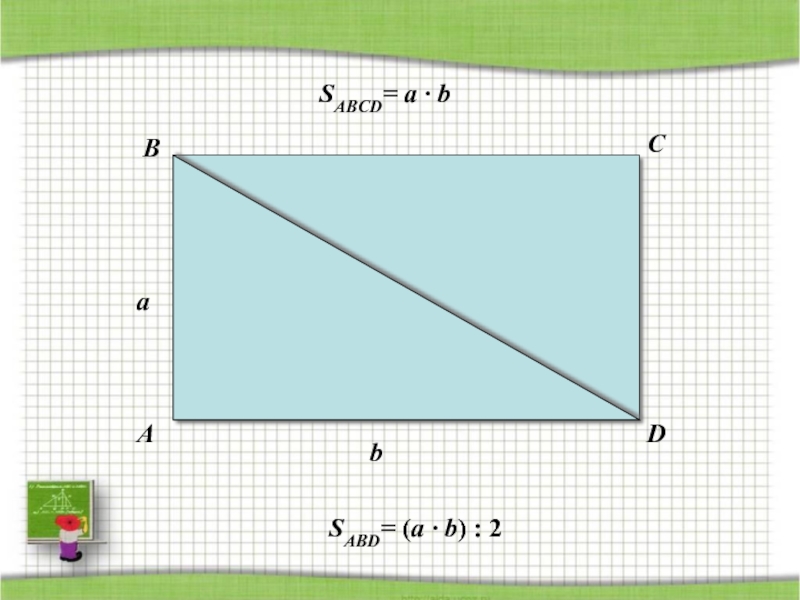
- 48. ABCDabSABCD= a · bSABD= (a · b) : 2Площадь прямоугольного треугольника
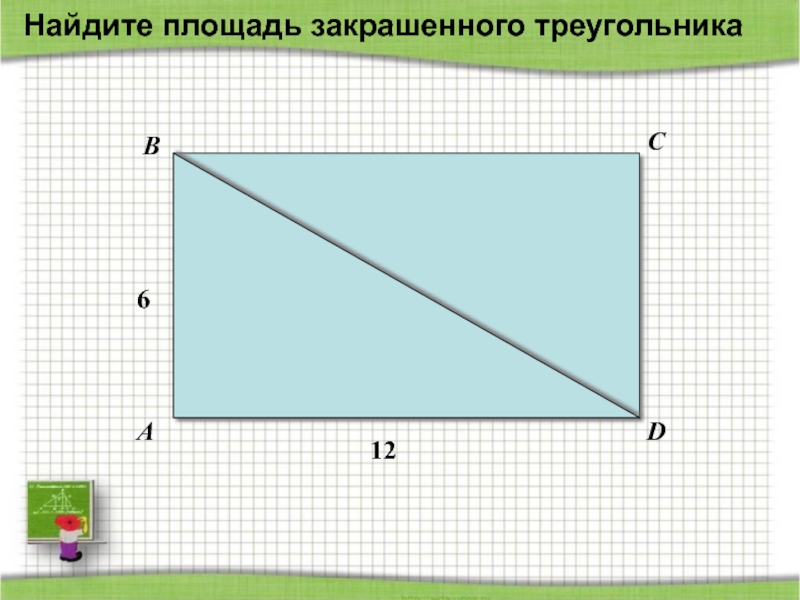
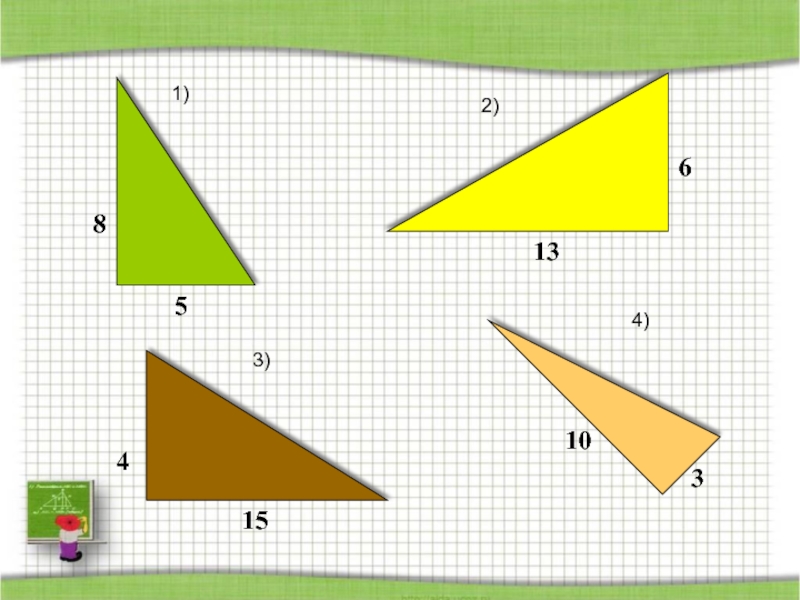
- 49. ABCD612Найдите площадь закрашенного треугольника
- 50. Найдите площадь треугольника1)2)3)4)
- 51. Проверь себя.1) 202) 393) 304) 15
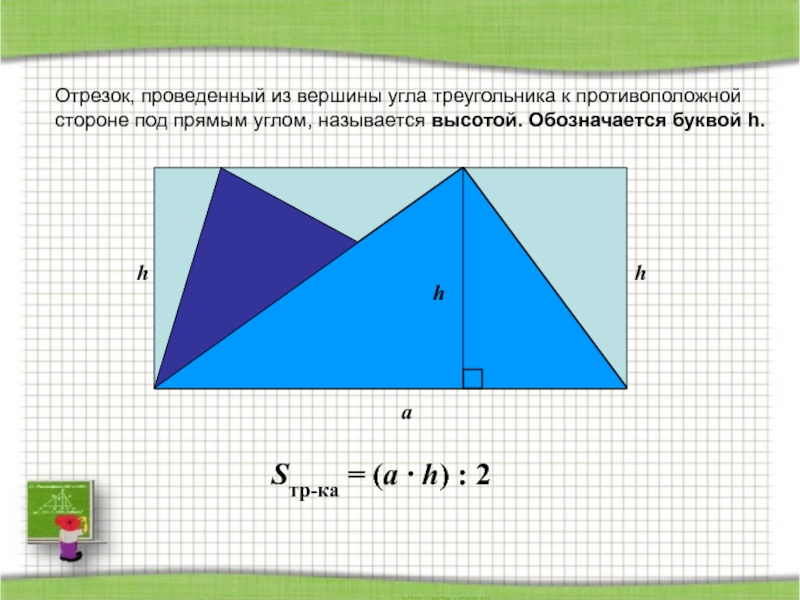
- 52. hhhaSтр-ка = (a · h) : 2Площадь
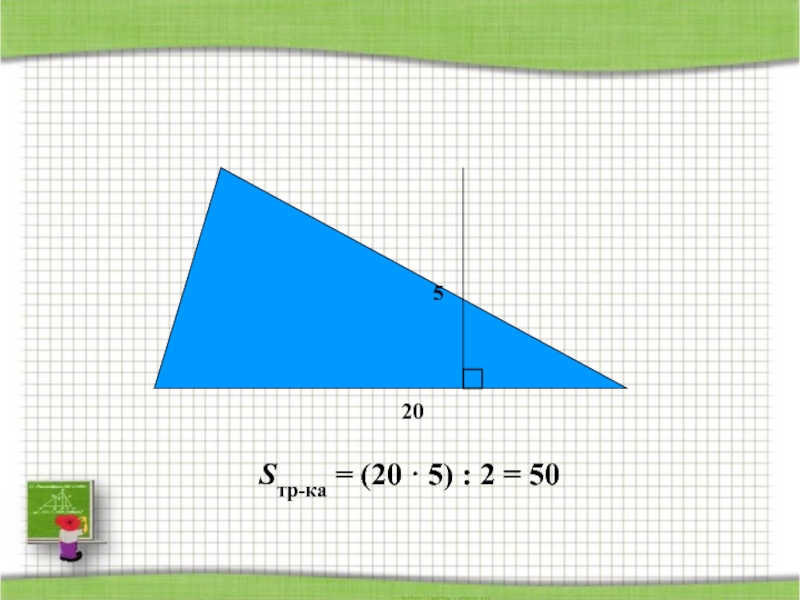
- 53. Найдите площадь треугольникаSтр-ка = (20 · 5) : 2 = 50
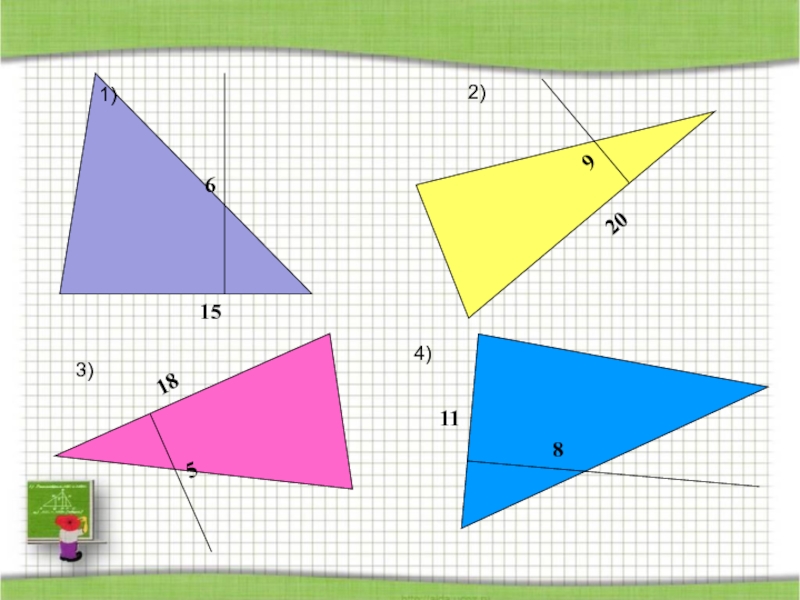
- 54. Найдите площадь треугольника1)2)4)3)
- 55. Проверь себя.1) 452) 903) 454) 44
- 56. Урок 7 Свойства углов треугольника.
- 57. Часто знает и дошкольник,Что такое треугольник.А уж
- 58. ЧЕМУ РАВНА СУММАУГЛОВ ТРЕУГОЛЬНИКА?
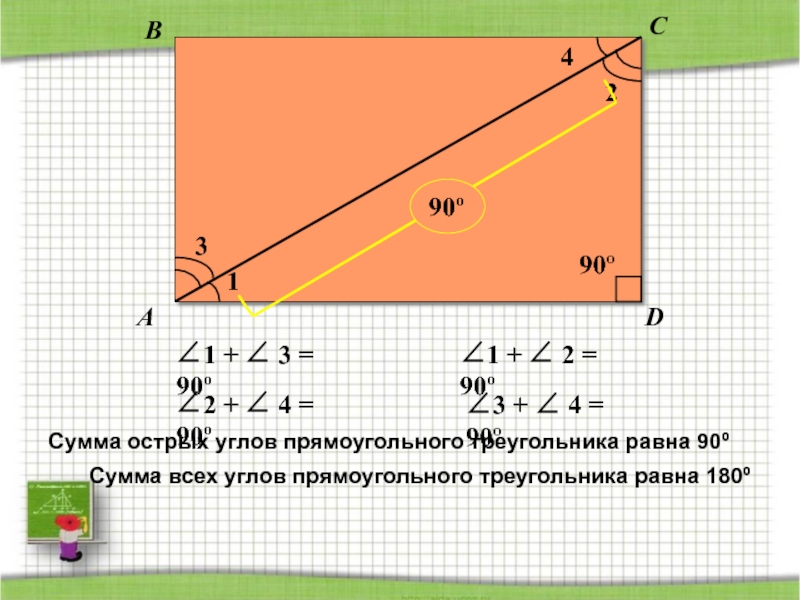
- 59. ABCD2431∠1 + ∠ 3 = 90º∠2 +
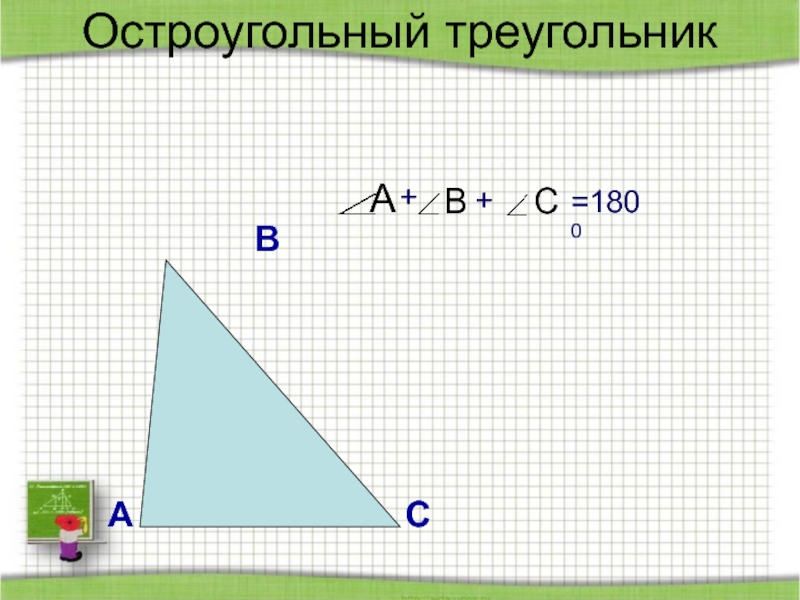
- 60. Остроугольный треугольникАВСА +ВС+=1800
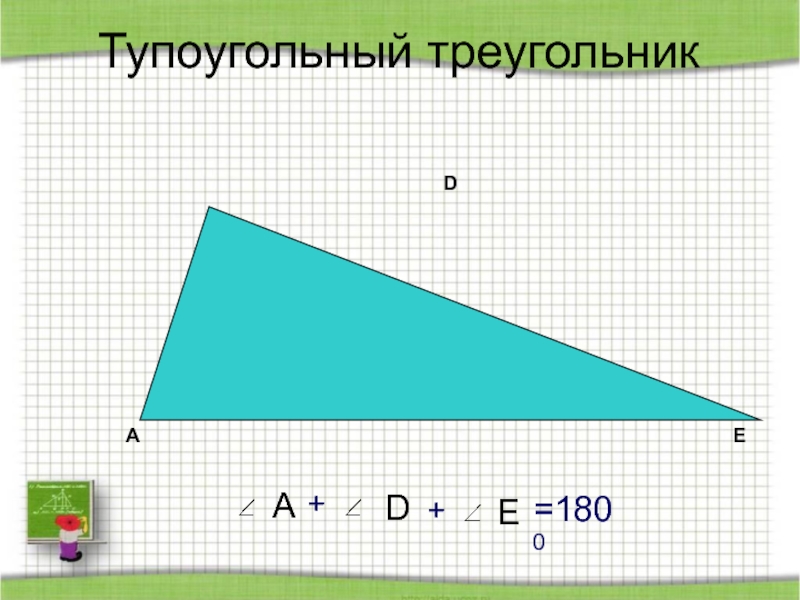
- 61. Тупоугольный треугольникADEА++DE=1800
- 62. Прямоугольный треугольникABC=1800ABC++
- 63. Вывод: Сумма углов треугольника равна1231 +2 +3 =18001800
- 64. Слайд 64
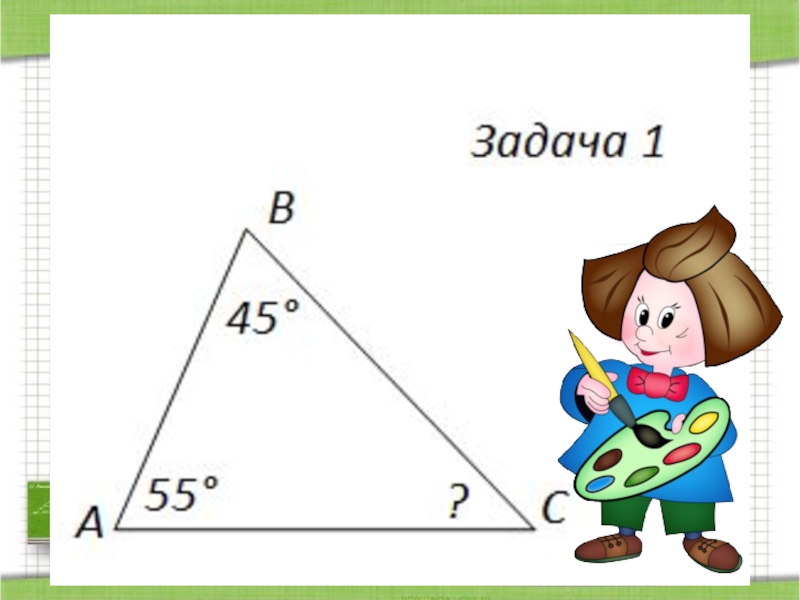
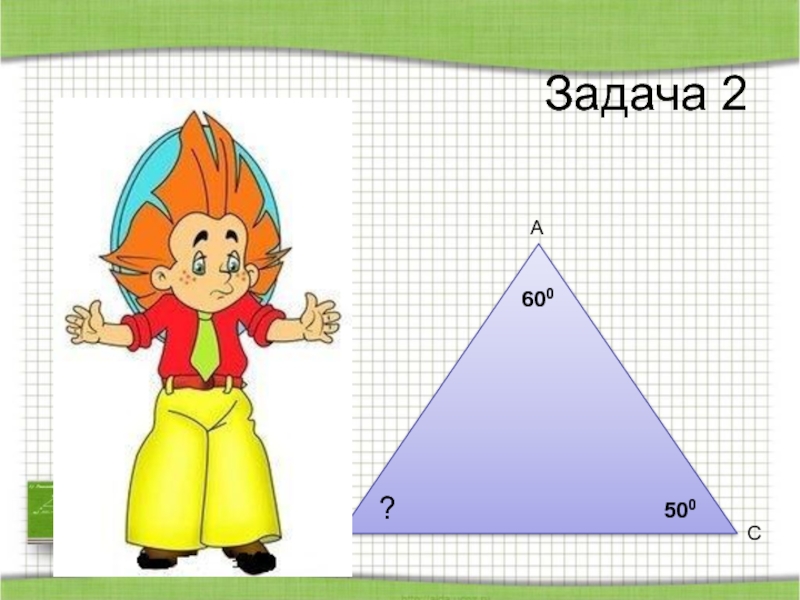
- 65. Задача 2500600?АВС
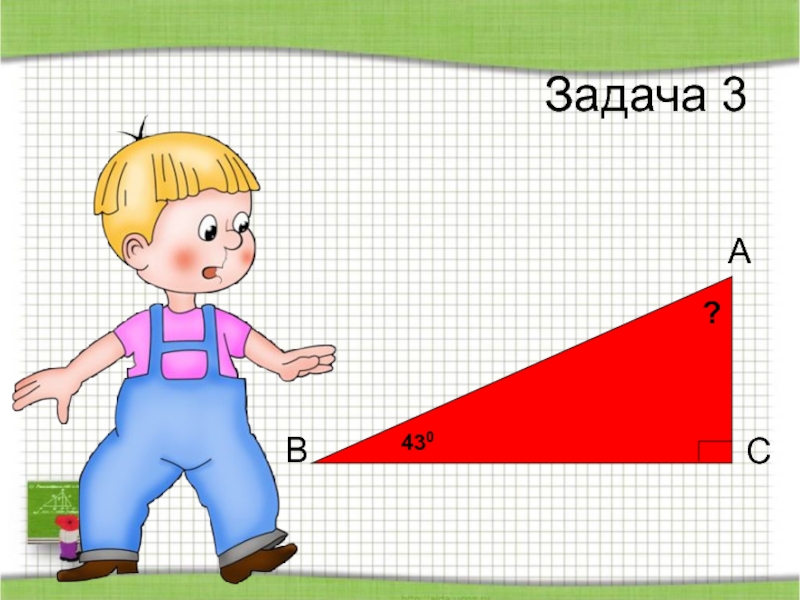
- 66. 430АВС?Задача 3
- 67. Слайд 67
- 68. Проверь себя.2) 1800 – 500 – 600
- 69. Задача Если треугольник существует, найдите его третий угол и определите вид треугольника ( заполните таблицу).
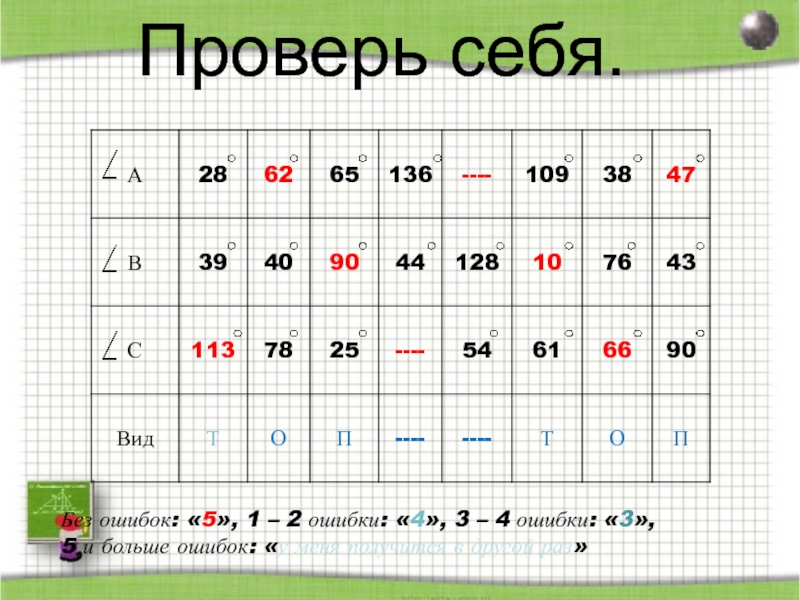
- 70. Проверь себя.Без ошибок: «5», 1 – 2
- 71. Урок 8 Расстояние между двумя точками. Масштаб.
- 72. О расстоянии нам приходиться говорить довольно часто.
- 73. Как вы знаете, расстояние между двумя точками
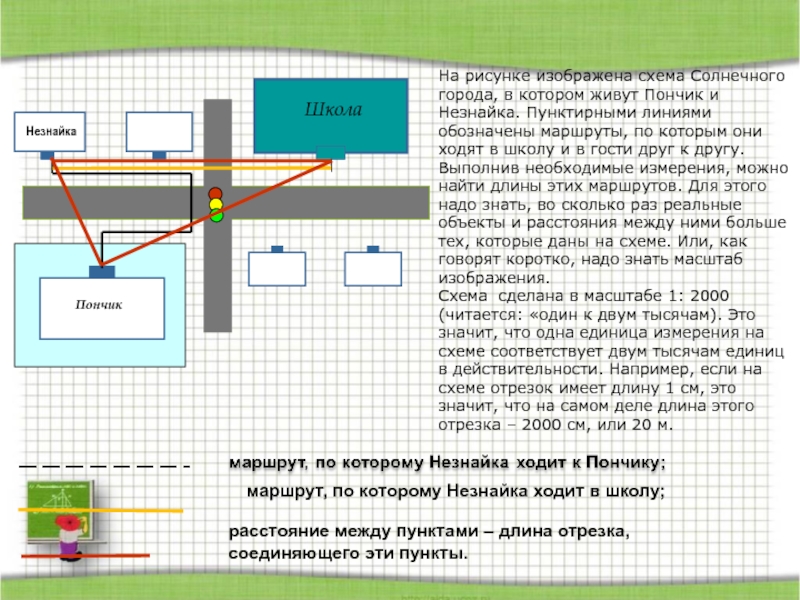
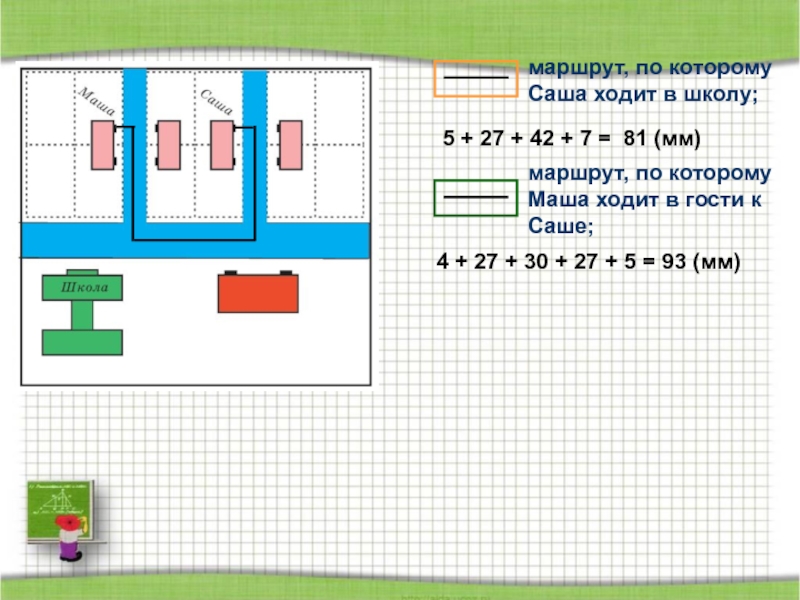
- 74. Незнайка ПончикДлина маршрута и расстояниеНа рисунке изображена
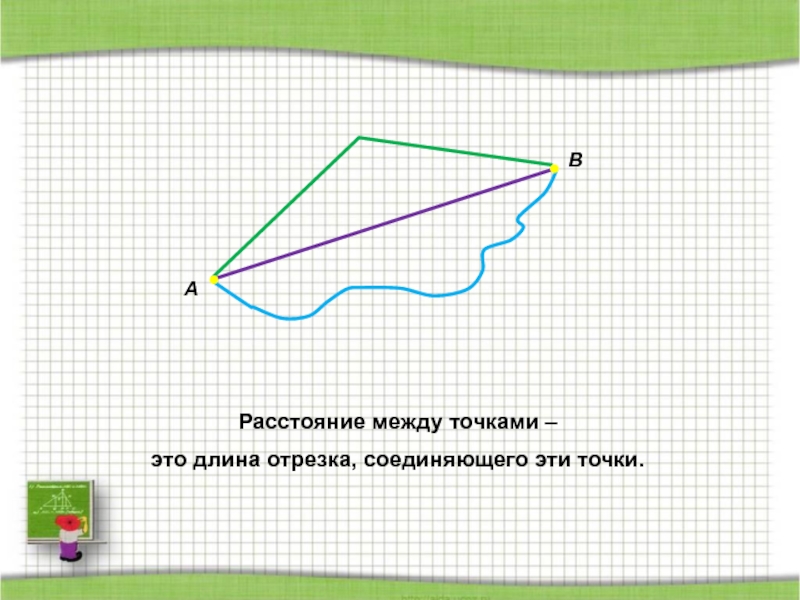
- 75. Расстояние между двумя точкамиРасстояние между точками – это длина отрезка, соединяющего эти точки.АВ
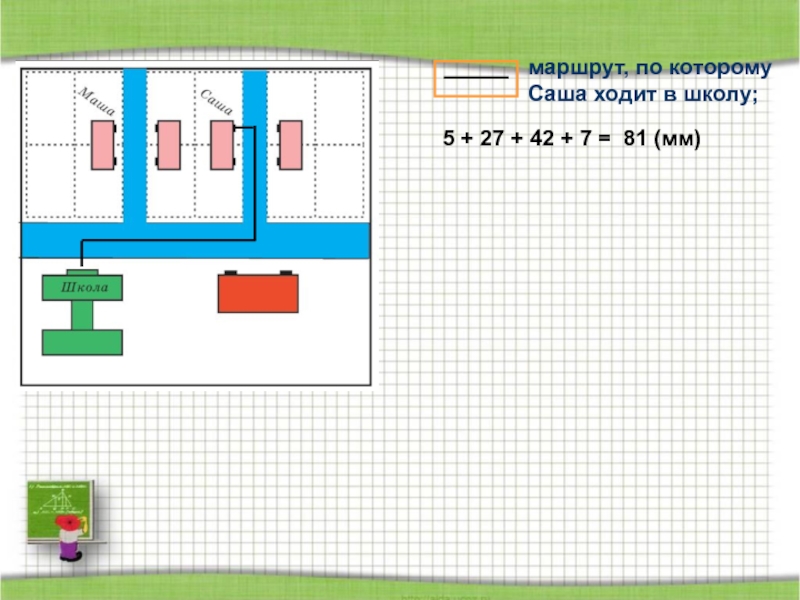
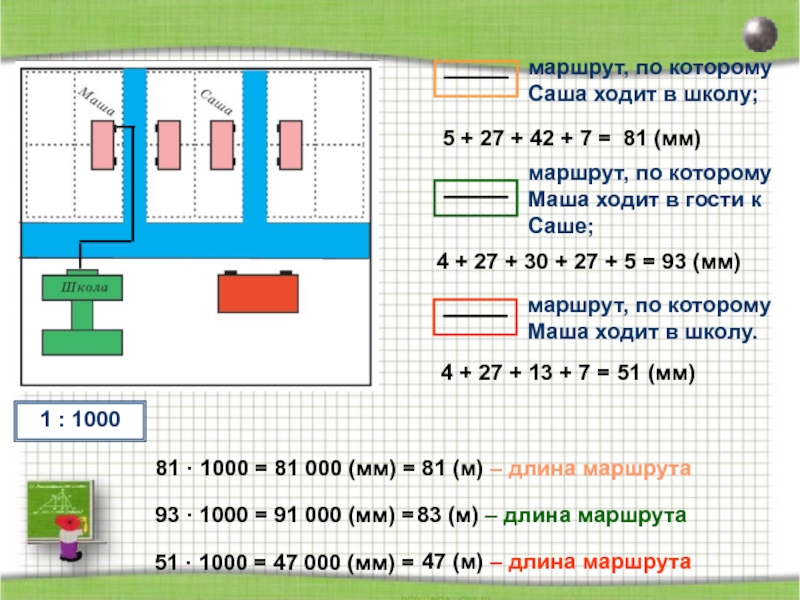
- 76. 5 + 27 + 42 + 7 =81 (мм)
- 77. 4 + 27 + 30 + 27 + 5 = 93 (мм)
- 78. 4 + 27 + 13 + 7
- 79. Урок 9 Расстояние от точки до прямой. Перпендикулярные прямые.
- 80. Незнайка и Пончик собрали грибы в лесу.
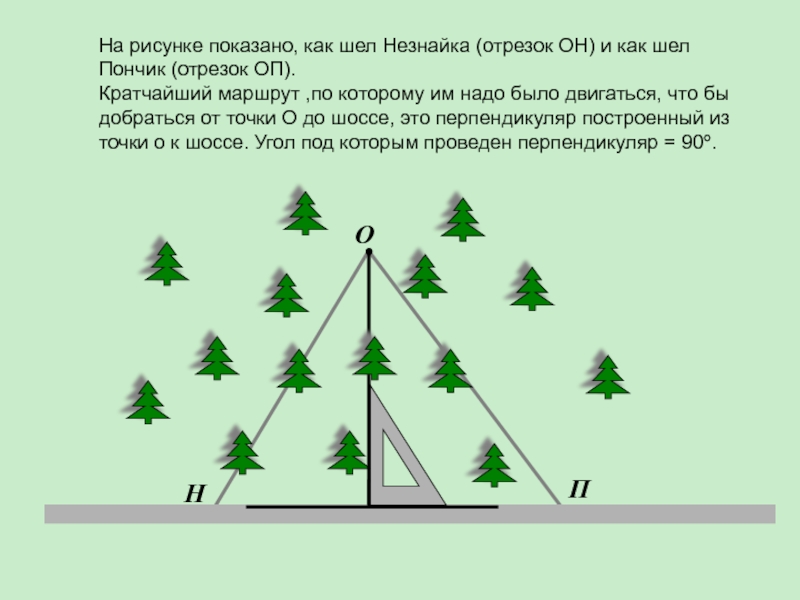
- 81. ОПННа рисунке показано, как шел Незнайка (отрезок
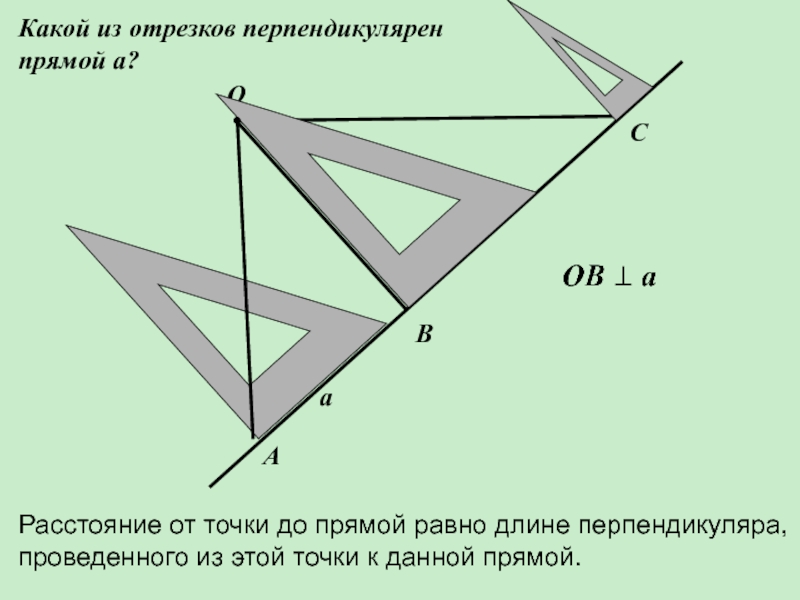
- 82. ОВАСаКакой из отрезков перпендикулярен прямой а?Расстояние от
- 83. Для построения перпендикуляра к прямой необходимо использовать прямоугольный треугольник и линейку.
- 84. DAaCBВзаимно перпендикулярные прямые – это прямые, которые пересекаются под прямым углом
- 85. Спасибо за внимание!
Слайд 2«Учиться можно только весело. Чтобы переваривать
Французский писатель XIX века Анатоль Франц однажды заметил, что:
Слайд 3Содержание
Определение угла. Развернутый угол.
Сравнение углов наложением.
Измерение углов.
Биссектриса угла.
Треугольник.
Площадь треугольника.
Свойства углов треугольника.
Расстояние
Расстояние от точки до прямой. Перпендикулярные прямые.
Слайд 6Развернутый угол.
Развернутый угол-это угол, образованный дополнительными лучами.
O A и O B
или противоположные лучи
A O B
Слайд 7Проверь себя.
Стороны угла - это два луча , которыми образован угол.
Луч
Давайте подумаем что такое сторона угла? И назовите стороны угла изображенного на рисунке.
Слайд 8Что такое вершина угла? Назовите вершины изображенных углов.
Проверь себя.
Вершина угла –это
(точка N;B;E)
Слайд 9Лучи ВА и ВС — это стороны угла, а точка В,
Обозначать угол можно двумя способами:
а) тремя буквами, причем буква, обозначающая вершину, пишется в середине — угол ABC,
б) одной буквой — той, которой обозначена вершина,- угол В.
Слово «угол» часто заменяют значком
Слайд 11Математический диктант
1 вариант
2 вариант
1.
б) запишите, как обозначена вершина данного угла:
в) запишите,
Слайд 13Проверьте себя:
1 вариант
2 вариант
1.
а) запишите название данного угла:
∠ MNP
∠ RST
б) запишите,
точка N
точка S
в) запишите, как обозначены стороны данного угла:
Слайд 15
Вы знаете, что равные фигуры можно совместить так, что они совпадут.
А как же сравнить два угла?
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Слайд 20
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
160
150
170
180
Одно деление транспортира = 1° (один градус)
1° (один градус) – единица
Слайд 24 2. Расположить транспортир так, чтобы одна из сторон угла проходила
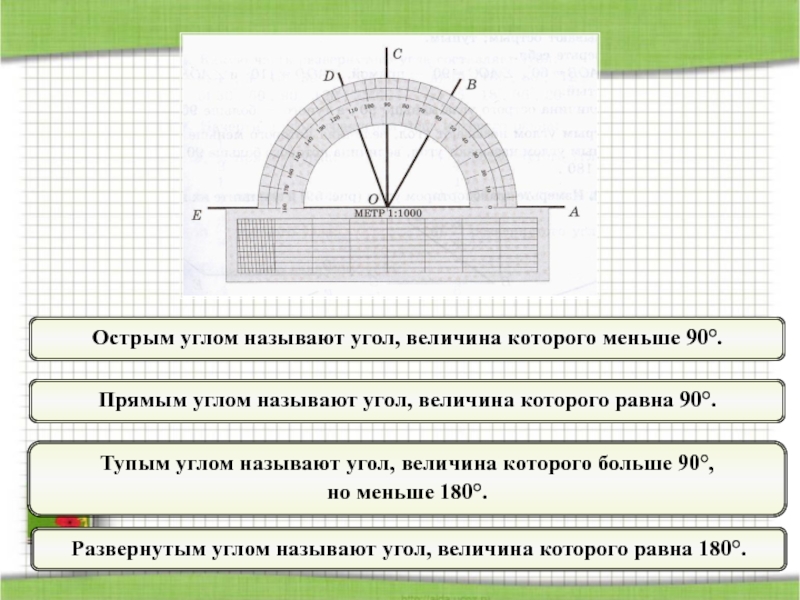
Слайд 29Прямым углом называют угол, величина которого равна 90°.
Тупым углом называют угол,
но меньше 180°.
Острым углом называют угол, величина которого меньше 90°.
Развернутым углом называют угол, величина которого равна 180°.
Слайд 30 Что нужно для того , чтобы измерить градусную меру угла?
1.
2.Составить алгоритм измерения углов.
3.Уметь точно определять градусную меру угла.
4.Уметь правильно определять вид угла.
5. Уметь точно вычислять градусную меру угла.
Слайд 31
Найти градусную меру угла, выполнив
вычисления, используя верхнюю и нижнюю
шкалу
1400
300
Проверка
1400 – 300 = 1100
Слайд 33Этот луч называется биссектрисой угла.
Вырежьте из бумаги угол и перегните так,
Слайд 35Биссектриса угла- это луч с началом в вершине угла, делящий угол
А я знаю стишок про биссектрису.
«Биссектриса- это крыса которая бегает по углам и делит угол пополам.»
Слайд 42
B
A
C
Остроугольный
Виды треугольников.
Остроугольный треугольник – это треугольник у которого все углы острые.
Слайд 46Правило треугольника:
«Сумма двух сторон треугольника
всегда больше третьей стороны»
4
6
7
4 < 6+7
6
7 < 4+6
Могут ли быть у треугольника стороны
равные 2,2 и 5?
Проверь себя. нет
Слайд 52
h
h
h
a
Sтр-ка = (a · h) : 2
Площадь треугольника
Отрезок, проведенный из вершины
Слайд 57Часто знает и дошкольник,
Что такое треугольник.
А уж Вам- то как не
Но совсем другое дело –
Очень быстро и умело
Величины все улов
В треугольнике узнать.
Слайд 59
A
B
C
D
2
4
3
1
∠1 + ∠ 3 = 90º
∠2 + ∠ 4 = 90º
∠1
∠3 + ∠ 4 = 90º
Сумма острых углов прямоугольного треугольника равна 90º
Сумма всех углов прямоугольного треугольника равна 180º
90º
Слайд 68Проверь себя.
2) 1800 – 500 – 600 = 700
1) 1800 –
3) 1800 – 900 – 430 = 470
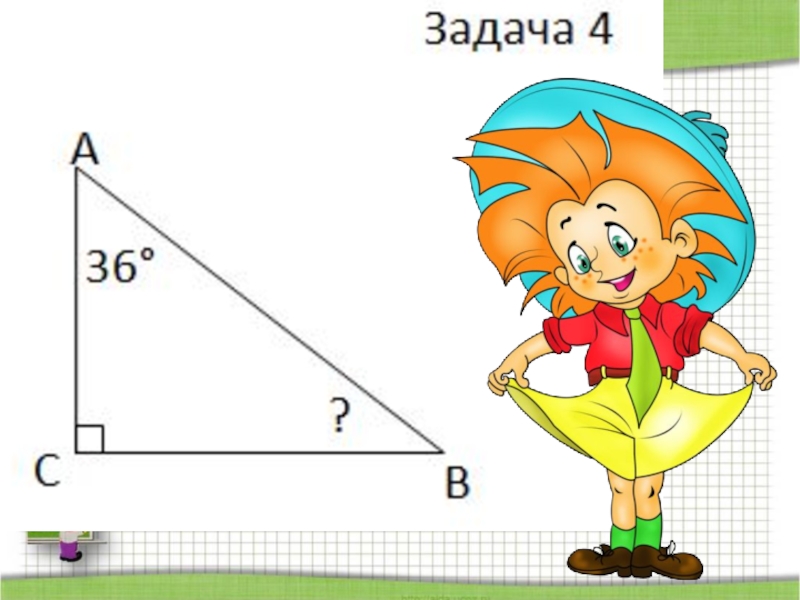
4) 1800 – 900 – 360 = 540
Слайд 69Задача
Если треугольник существует, найдите его третий угол и определите вид
Слайд 70Проверь себя.
Без ошибок: «5», 1 – 2 ошибки: «4», 3 –
5 и больше ошибок: «у меня получится в другой раз»
Слайд 72О расстоянии нам приходиться говорить довольно часто. И следует заметить, что
Рассмотрим такой пример: Незнайка живет в 7 минутах ходьбы от школы, а Пончик идет от дома до школы 5 минут. Можно ли утверждать, что Пончик живет ближе к школе, чем Незнайка? Может ли Пончик жить дальше от школы, чем Незнайка? Итак, в этом примере мы сделали попытку измерить расстояние в минутах и выяснили, что точность такого измерения крайне мала, поскольку у нас не было информации о скоростях движения Пончика и Незнайки.
Слайд 73Как вы знаете, расстояние между двумя точками измеряется по соединяющей их
Слайд 74
Незнайка
Пончик
Длина маршрута и расстояние
На рисунке изображена схема Солнечного города, в
Слайд 75Расстояние между двумя точками
Расстояние между точками –
это длина отрезка, соединяющего
А
В
Слайд 784 + 27 + 13 + 7 =
1 : 1000
81 ·
93 · 1000 = 91 000 (мм) =
51 · 1000 = 47 000 (мм) =
83 (м) – длина маршрута
51 (мм)
47 (м) – длина маршрута
= 81 (м) – длина маршрута
Слайд 80Незнайка и Пончик собрали грибы в лесу. После того как корзинки
Слайд 81
О
П
Н
На рисунке показано, как шел Незнайка (отрезок ОН) и как шел
Кратчайший маршрут ,по которому им надо было двигаться, что бы добраться от точки О до шоссе, это перпендикуляр построенный из точки о к шоссе. Угол под которым проведен перпендикуляр = 90º.