прекрасного»
Аристотель
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Призмы (урок - семинар)
Содержание
- 1. Призмы (урок - семинар)
- 2. В начале урока мне хотелось бы продемонстрировать
- 3. Ландшафтный дизайн
- 4. Дизайн одежды
- 5. Дизайн одежды
- 6. Дизайн интерьеров
- 7. Дизайн интерьеров
- 8. Дизайн интерьеров
- 9. Дизайн в архитектуре
- 10. Дизайн в архитектуре
- 11. Что общего у всех этих дизайнерских решений?
- 12. ПРАВИЛЬНО!При создании этих дизайн проектов применялись различные объемные геометрические фигуры!
- 13. Такой стиль творчества использовался даже в искусстве!
- 14. Английский искусствовед Эрнст ГомбрихАнглийский искусствовед Эрнст Гомбрих выводит истоки
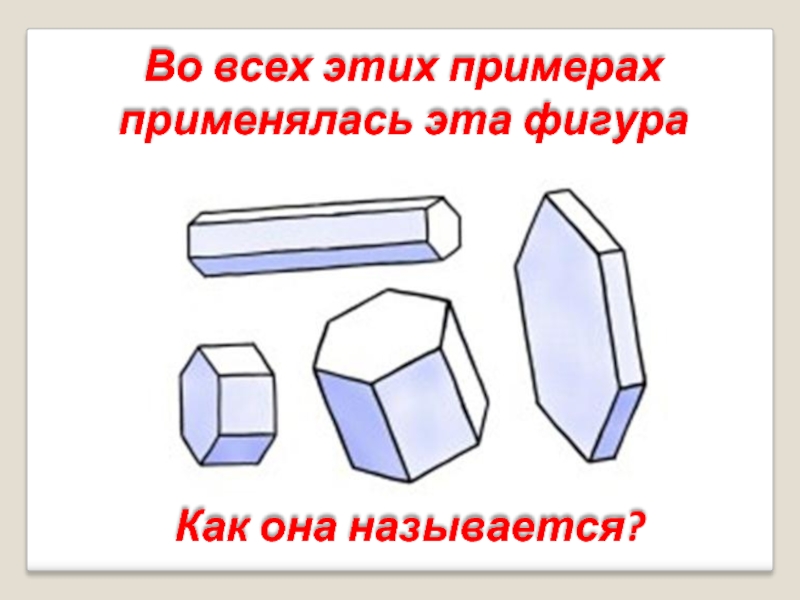
- 15. Во всех этих примерах применялась эта фигураКак она называется?
- 16. ПРАВИЛЬНО!Итак тема сегодняшнего занятияПРАВИЛЬНО!ПРИЗМА
- 17. МногогранникМногогранник, поверхность которого состоит из двух равных
- 18. Высота - это перпендикулярпроведенный из какой–нибудь точки
- 19. Все призмы делятся на прямые и наклонные.Если
- 20. Правильной призмой называется прямая призма, основаниями которой являются правильные многоугольники.Правильная призма
- 21. Задача № 1Сторона правильной четырехугольной призмы равна
- 22. Задача № 2Площадь сечения правильной призмы плоскостью,
- 23. Задача № 3Сторона основания правильной треугольной призмы
- 24. Творческая работа
- 25. Золотое сечение в дизайне основывается на таком принципе.
- 26. Оказывается, золотое сечение имеет численное выражение. Его
- 27. IPod Shuffle и iPhone4 1.7 за первые
- 28. Участвуют три команды по количеству рядов. В
- 29. Проведите анализ сегодняшнего занятия и заполните карточки.Рефлексия
В начале урока мне хотелось бы продемонстрировать Вам некоторые дизайнерские решения в разных областях применения. Вы внимательно посмотрите, проанализируйте и в конце демонстрации расскажите , что у всех этих проектов есть общего.Ландшафтный дизайн
Слайд 2В начале урока мне хотелось бы продемонстрировать Вам некоторые дизайнерские решения
в разных областях применения. Вы внимательно посмотрите, проанализируйте и в конце демонстрации расскажите , что у всех этих проектов есть общего.
Ландшафтный дизайн
Слайд 12ПРАВИЛЬНО!
При создании этих дизайн проектов применялись различные объемные геометрические фигуры!
Слайд 13Такой стиль творчества использовался даже в искусстве! Кубизм (фр. (фр. Cubisme) — модернистское (фр. Cubisme) — модернистское направление в
изобразительном искусстве, прежде всего в живописи, зародившееся в начале XX века во Франции и характеризующееся использованием подчёркнуто геометризованных условных форм, стремлением «раздробить» реальные объекты на стереометрические примитивы.
Слайд 14
Английский искусствовед Эрнст ГомбрихАнглийский искусствовед Эрнст Гомбрих выводит истоки кубизма из творчества французского
художника Поля Сезанна, приводя как пример его работы «Гора Сент-Виктуар со стороны Бельвю» и «Горы в Провансе», а также его ответ на письмо молодого Пабло Пикассо: «В одном из писем Сезанн рекомендует молодому художнику рассматривать натуру как совокупность простых форм — сфер, конусов, цилиндров. Он имел в виду, что эти базисные формы необходимо держать в сознании как организующее начало картины. Однако Пикассо и его друзья восприняли совет буквально».
Возникновение кубизма традиционно датируют 1906Возникновение кубизма традиционно датируют 1906—1907 годамиВозникновение кубизма традиционно датируют 1906—1907 годами и связывают с творчеством Пабло ПикассоВозникновение кубизма традиционно датируют 1906—1907 годами и связывают с творчеством Пабло Пикассо и Жоржа БракаВозникновение кубизма традиционно датируют 1906—1907 годами и связывают с творчеством Пабло Пикассо и Жоржа Брака. Термин «кубизм» появился в 1908 годуВозникновение кубизма традиционно датируют 1906—1907 годами и связывают с творчеством Пабло Пикассо и Жоржа Брака. Термин «кубизм» появился в 1908 году, после того как художественный критик Луи ВосельВозникновение кубизма традиционно датируют 1906—1907 годами и связывают с творчеством Пабло Пикассо и Жоржа Брака. Термин «кубизм» появился в 1908 году, после того как художественный критик Луи Восель назвал новые картины Брака «кубическими причудами». (фр. bizarreries cubiques).
Возникновение кубизма традиционно датируют 1906Возникновение кубизма традиционно датируют 1906—1907 годамиВозникновение кубизма традиционно датируют 1906—1907 годами и связывают с творчеством Пабло ПикассоВозникновение кубизма традиционно датируют 1906—1907 годами и связывают с творчеством Пабло Пикассо и Жоржа БракаВозникновение кубизма традиционно датируют 1906—1907 годами и связывают с творчеством Пабло Пикассо и Жоржа Брака. Термин «кубизм» появился в 1908 годуВозникновение кубизма традиционно датируют 1906—1907 годами и связывают с творчеством Пабло Пикассо и Жоржа Брака. Термин «кубизм» появился в 1908 году, после того как художественный критик Луи ВосельВозникновение кубизма традиционно датируют 1906—1907 годами и связывают с творчеством Пабло Пикассо и Жоржа Брака. Термин «кубизм» появился в 1908 году, после того как художественный критик Луи Восель назвал новые картины Брака «кубическими причудами». (фр. bizarreries cubiques).
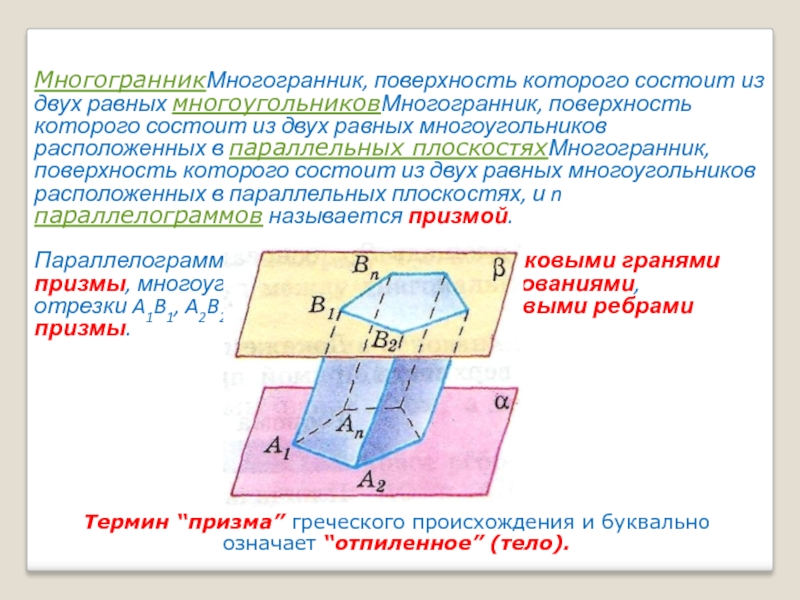
Слайд 17МногогранникМногогранник, поверхность которого состоит из двух равных многоугольниковМногогранник, поверхность которого состоит
из двух равных многоугольников расположенных в параллельных плоскостяхМногогранник, поверхность которого состоит из двух равных многоугольников расположенных в параллельных плоскостях, и n параллелограммов называется призмой.
Параллелограммы A1 B1 B2 A2 называются боковыми гранями призмы, многоугольники A1A2A3 …An– ее основаниями,
отрезки A1B1, A2B2,, …Аn Вn называются боковыми ребрами призмы.
Термин “призма” греческого происхождения и буквально означает “отпиленное” (тело).
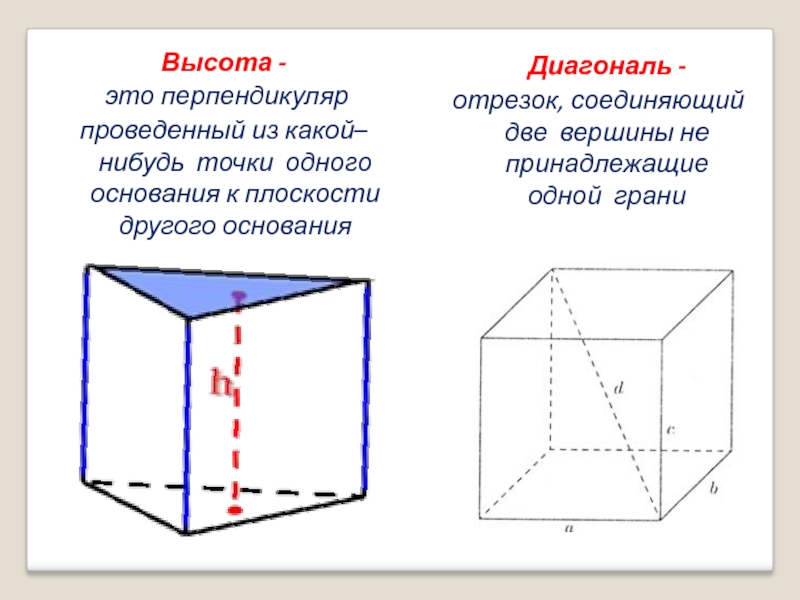
Слайд 18Высота -
это перпендикуляр
проведенный из какой–нибудь точки одного основания к плоскости
другого основания
Диагональ -
отрезок, соединяющий две вершины не принадлежащие одной грани
Слайд 19Все призмы делятся на прямые и наклонные.
Если боковое ребро призмы перпендикулярно
плоскости ее основания, то такую призму называют прямой; если боковое ребро призмы не перпендикулярно плоскости ее основания, то такую призму называют наклонной. У прямой призмы боковые грани - прямоугольники.
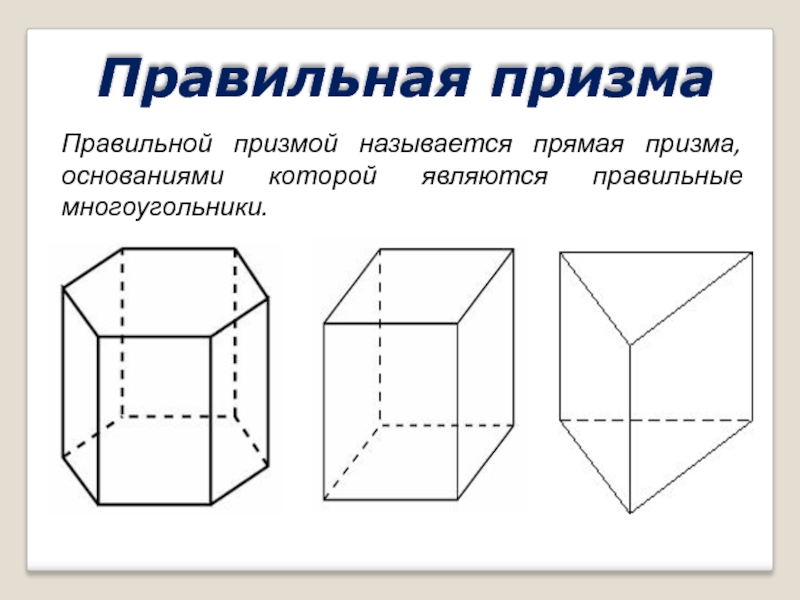
Слайд 20Правильной призмой называется прямая призма, основаниями которой являются правильные многоугольники.
Правильная призма
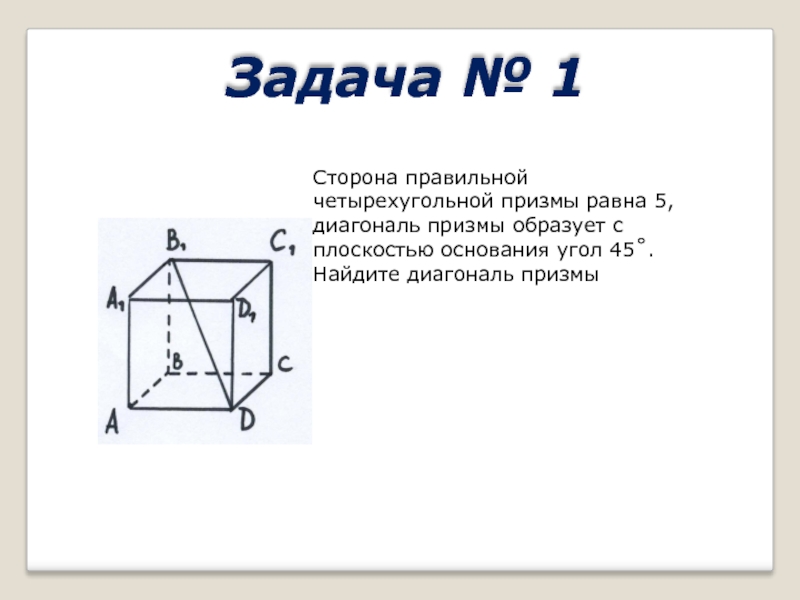
Слайд 21Задача № 1
Сторона правильной четырехугольной призмы равна 5, диагональ призмы образует
с плоскостью основания угол 45˚. Найдите диагональ призмы
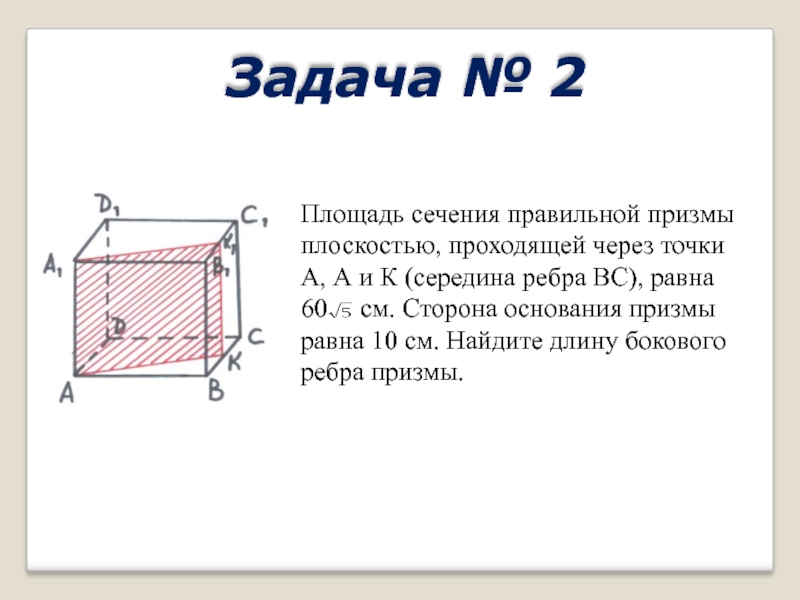
Слайд 22Задача № 2
Площадь сечения правильной призмы плоскостью, проходящей через точки А,
А и К (середина ребра ВС), равна 60 см. Сторона основания призмы равна 10 см. Найдите длину бокового ребра призмы.
Слайд 23Задача № 3
Сторона основания правильной треугольной призмы равна 8 см., боковое
ребро равно 6 см. Найдите площадь сечения проходящего через сторону нижнего основания и противоположную вершину верхнего основания.
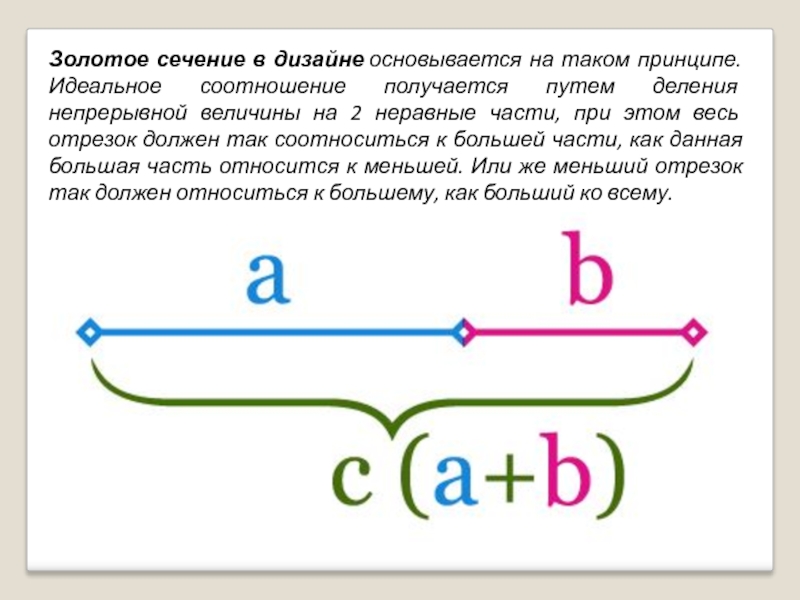
Слайд 25Золотое сечение в дизайне основывается на таком принципе. Идеальное соотношение получается путем
деления непрерывной величины на 2 неравные части, при этом весь отрезок должен так соотноситься к большей части, как данная большая часть относится к меньшей. Или же меньший отрезок так должен относиться к большему, как больший ко всему.
Слайд 26Оказывается, золотое сечение имеет численное выражение. Его легко определить при помощи
ряда Фибоначчи. Возможно, кто-то помнит его еще из школьного курса. Так вот, отношение золотого сечения равно 1,618 – именно к нему стремятся соотношения чисел в ряде знаменитого итальянского математика. Поэтому дизайнеры чаще всего и применяют ряд Фибоначчи для вычисления идеальных пропорций. Но прогресс не стоит на месте, и сегодня появились специальные чрезвычайно удобные программы, позволяющие с легкостью вычислять золотое сечение. Вам нужно лишь задать число и получить соответствующее значение.
Слайд 27IPod Shuffle и iPhone4 1.7 за первые 4 дня продаж принесли
своим разработчикам бешеную прибыль, ведь их было продано фактически 2 миллиона моделей. А соотношение сторон у них 1,59 и 1,67 соответственно
Слайд 28Участвуют три команды по количеству рядов. В каждой команде я назначаю
капитана.
1 ряд. Вы будете дизайнерами одежды.
2 ряд. Вы будете ландшафтными дизайнерами.
3 ряд. Вы будете дизайнерами интерьеров.
Задачи создать соответствующий дизайн – проект, при этом желательно и учитывать правило «золотого сечения».
1 ряд. Вы будете дизайнерами одежды.
2 ряд. Вы будете ландшафтными дизайнерами.
3 ряд. Вы будете дизайнерами интерьеров.
Задачи создать соответствующий дизайн – проект, при этом желательно и учитывать правило «золотого сечения».
Задание