«Введение в вероятность» 5 класс
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Введение в вероятность. 5 класс
Содержание
- 1. Презентация Введение в вероятность. 5 класс
- 2. Опытом, или испытанием, называют осуществление определенного комплекса
- 3. Примеры:
- 4. Классификация событий: Достоверное событие – это событие, которое
- 5. Классификация событий: Невозможное событие – это событие, которое
- 6. Классификация событий: Случайное событие – это событие, которое
- 7. Классификация событий: Два события называются совместными в данном
- 8. Классификация событий: Два события называются не совместными в
- 9. Классификация событий: Два события называются противоположными в данном
- 10. Комбинаторика - это раздел математики, в котором изучаются способы подсчета числа различных комбинаций.Основные типы комбинаций:перестановки;размещения;сочетания.
- 11. Комбинации, состоящие из одних и тех же
- 12. Комбинации, состоящие из n различных элементов по
- 13. Комбинации, состоящие из n различных элементов по
- 14. Задания для самостоятельного выполнения: Даны элементы a,
- 15. Основные правила комбинаторикиПравило сложения.Если элемент а можно
- 16. Основные правила комбинаторикиПравило умножения.Если элемент а можно
- 17. Пример решения задачи:Запишите все трехзначные числа, для
- 18. Задачи для самостоятельного изучения и решения № 96, 228, 388, 694№ 12, 27, 283
Опытом, или испытанием, называют осуществление определенного комплекса условий или действий, при которых происходит соответствующее явление. Возможный результат опыта называют событием.
Слайд 2 Опытом, или испытанием, называют осуществление определенного комплекса условий или действий, при
которых происходит соответствующее явление.
Возможный результат опыта называют событием.
Возможный результат опыта называют событием.
Слайд 4Классификация событий:
Достоверное событие – это событие, которое обязательно произойдет в этом
опыте.
Пример: в урне находятся красные шары. Событие «Извлеченный шар красный» – достоверное, так как в урне нет шаров другого цвета.
Пример: в урне находятся красные шары. Событие «Извлеченный шар красный» – достоверное, так как в урне нет шаров другого цвета.
Слайд 5Классификация событий:
Невозможное событие – это событие, которое не может произойти в
этом опыте.
Пример: в урне находятся красные шары. Событие «Извлеченный шар белый» – невозможное, так как в урне нет шаров белого цвета.
Пример: в урне находятся красные шары. Событие «Извлеченный шар белый» – невозможное, так как в урне нет шаров белого цвета.
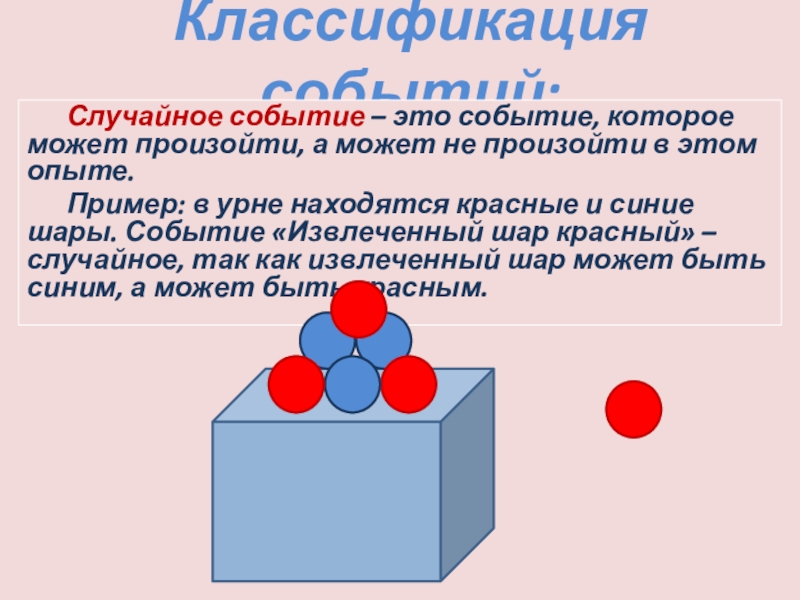
Слайд 6Классификация событий:
Случайное событие – это событие, которое может произойти, а может
не произойти в этом опыте.
Пример: в урне находятся красные и синие шары. Событие «Извлеченный шар красный» – случайное, так как извлеченный шар может быть синим, а может быть красным.
Пример: в урне находятся красные и синие шары. Событие «Извлеченный шар красный» – случайное, так как извлеченный шар может быть синим, а может быть красным.
Слайд 7Классификация событий:
Два события называются совместными в данном опыте если они оба
могут произойти в этом опыте.
Пример: подбрасывают две монеты.
События:
«Герб» на верхней стороне одной монеты» и
«Герб» на верхней стороне другой монеты» – совместные, так как появление одного события не исключает появление другого в этом опыте.
Пример: подбрасывают две монеты.
События:
«Герб» на верхней стороне одной монеты» и
«Герб» на верхней стороне другой монеты» – совместные, так как появление одного события не исключает появление другого в этом опыте.
Слайд 8Классификация событий:
Два события называются не совместными в данном опыте, если они
оба не могут произойти в этом опыте.
Пример: стрелок делает один выстрел по мишени.
События: «Попадание в мишень» и «Промах» – не совместные, так как стрелок либо попал в мишень, либо не попал в этом опыте.
Пример: стрелок делает один выстрел по мишени.
События: «Попадание в мишень» и «Промах» – не совместные, так как стрелок либо попал в мишень, либо не попал в этом опыте.
Слайд 9Классификация событий:
Два события называются противоположными в данном опыте если появление одного
из них равносильно непоявлению другого в этом опыте.
Пример: подбрасывают одну монету.
События:
«Герб» на верхней стороне монеты» и
«Цифра» на верхней стороне монеты» –
противоположные, так как появление одного события исключает появление другого в этом опыте.
Пример: подбрасывают одну монету.
События:
«Герб» на верхней стороне монеты» и
«Цифра» на верхней стороне монеты» –
противоположные, так как появление одного события исключает появление другого в этом опыте.
Слайд 10Комбинаторика -
это раздел математики, в котором изучаются способы подсчета числа
различных комбинаций.
Основные типы комбинаций:
перестановки;
размещения;
сочетания.
Слайд 11 Комбинации, состоящие из одних и тех же различных элементов и отличающиеся
друг от друга только их порядком, называются перестановками этих элементов.
Задание:
Даны элементы a, b, c. Определить число всевозможных перестановок (Р) из этих элементов.
Р = 6
Слайд 12 Комбинации, состоящие из n различных элементов по m элементов, отличающиеся друг
от друга либо порядком, либо составом, называются размещениями из этих элементов.
Задание:
Даны элементы a, b, c. Определить число всевозможных размещений (А) из трех элементов по два элемента.
А = 6
Слайд 13 Комбинации, состоящие из n различных элементов по m элементов, отличающиеся друг
от друга только составом, называются сочетаниями из этих элементов.
Задание:
Даны элементы a, b, c. Определить число всевозможных размещений (С) из трех элементов по два элемента.
С = 3
Слайд 14Задания для
самостоятельного выполнения:
Даны элементы a, b, c, d. Определить
число всевозможных перестановок (Р) из этих элементов.
Определить число всевозможных размещений (А) и сочетаний (С) из четырех элементов по два элемента.
Слайд 15Основные правила комбинаторики
Правило сложения.
Если элемент а можно выбрать n способами, а
элемент b можно выбрать m способами, то выбор «а или b» можно осуществить n + m способами.
Пример.
На полке стоят 3 диска с мультфильмами и 5 дисков с художественными фильмами. Дима хочет просмотреть один диск. Сколько вариантов существует для просмотра?
Решение: 3 + 5 = 8 вариантов просмотра.
Слайд 16Основные правила комбинаторики
Правило умножения.
Если элемент а можно выбрать n способами, после
чего элемент b можно выбрать m способами, то выбор «а и b» можно осуществить n · m способами.
Пример.
На полке стоят 3 диска с мультфильмами и 5 дисков с художественными фильмами. Дима хочет просмотреть один диск с мультфильмом и один диск с художественным фильмом. Сколько вариантов существует для просмотра?
Решение: 3 · 5 = 15 вариантов просмотра.
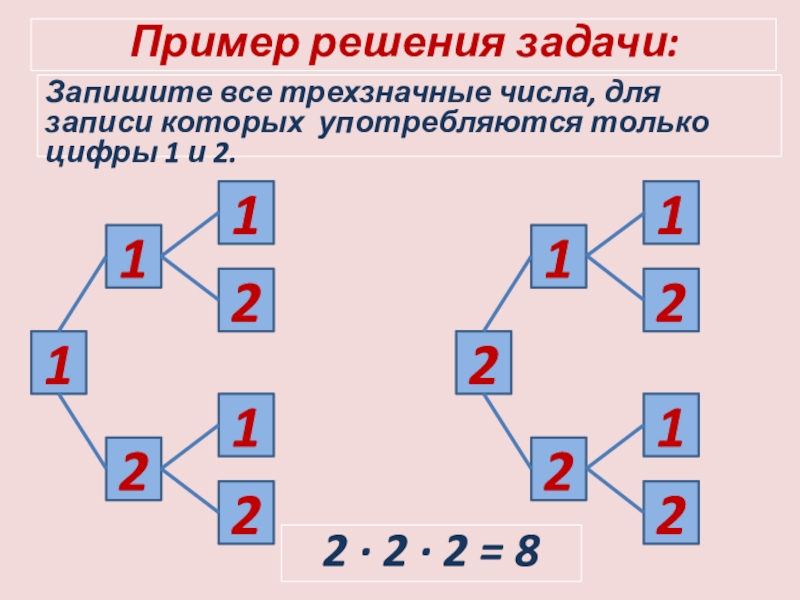
Слайд 17Пример решения задачи:
Запишите все трехзначные числа, для записи которых употребляются только
цифры 1 и 2.
1
1
2
1
1
2
2
2
1
2
1
2
1
2
2 · 2 · 2 = 8
