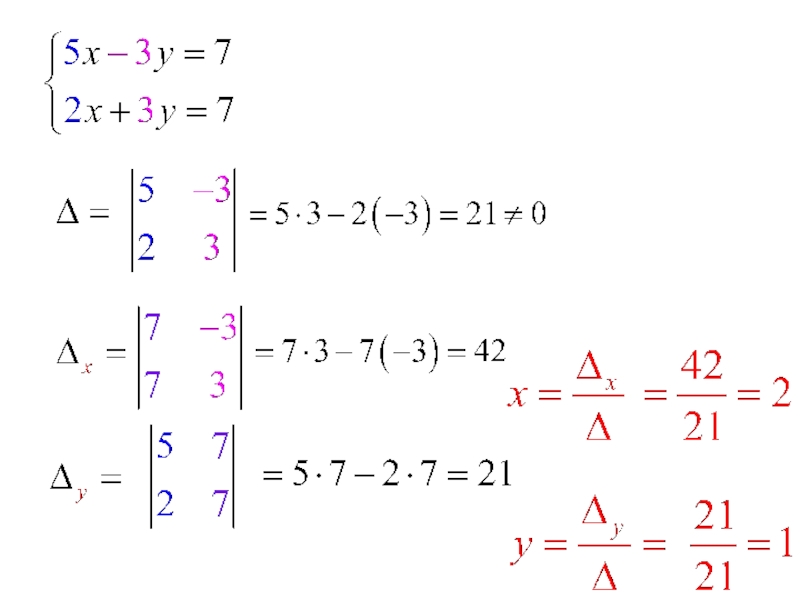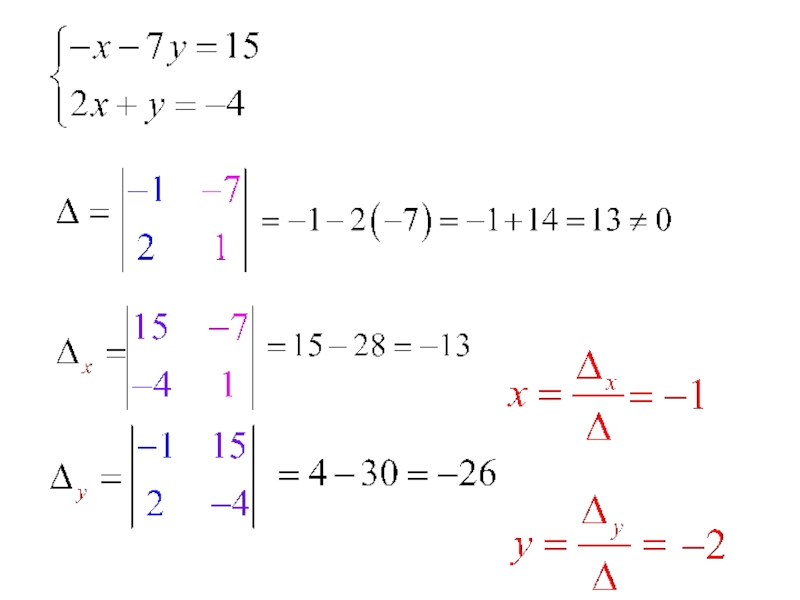Презентация, доклад урока Решение системы линейных уравнений с тремя переменными

Содержание

1. Презентация урока Решение системы линейных уравнений с тремя переменными
2. Системой уравнений с двумя
3. Методы решения системы уравненийМетод подстановки;Метод сложения;Графический метод;Метод Крамера
4. Метод Крамера
5. Габриель Крамер (нем. Gabriel Cramer, 31
6. Метод КрамераОпределениеМатрицей размеров mxn называется прямоугольная таблица
7. Метод КрамераМатрица
8. Метод КрамераМатрицаЭлементы a1 и b2 образуют главную диагональ Элементы b1 и a2образуют побочную диагональ
9. Определитель матрицы второго порядкаОпределителем матрицы второго порядка
10. Определитель матрицы
11. Определитель матрицы
12. Определитель матрицы
13. Свойства определителей:Если в определителе какие-либо две строки
14. Решение систем линейных уравнений с двумя переменными
15. Решение систем уравнений с двумя переменными
16. Решение систем уравнений с двумя переменными
17. Решение систем уравнений с двумя переменными
18. Решение систем уравнений с двумя переменными
19. Решение систем уравнений с двумя переменными
20. Решение систем уравнений с двумя переменными
21. Решение систем уравнений с двумя переменными
22. Решение систем уравнений с двумя переменными
23. Решение систем уравнений с двумя переменными
24. Решение систем уравнений с двумя переменными
25. Слайд 25
26. Слайд 26
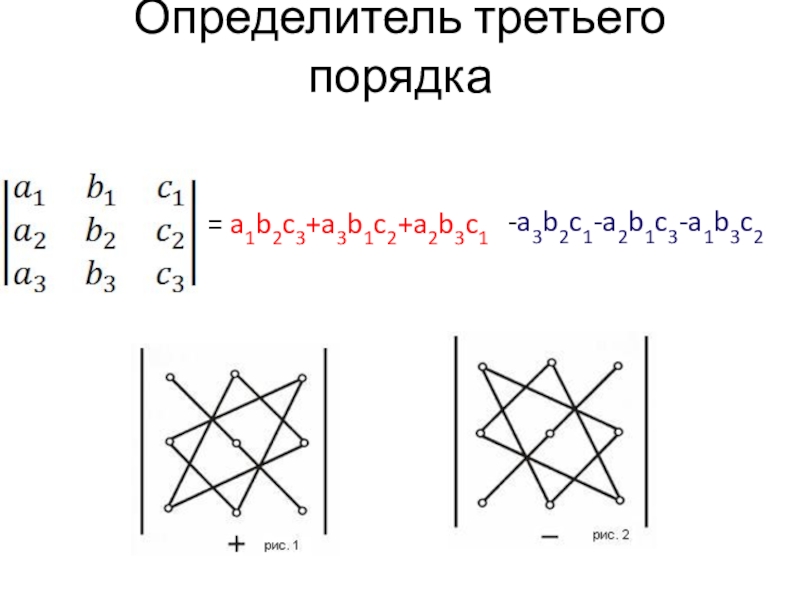
27. Системы трёх линейных уравнений. Определитель третьего порядка
28. 4.20 а)(-2) б) 1/6 в) 0 г) 0а)(2;1) б) (3;2) в) (1;2) г) ᴓ
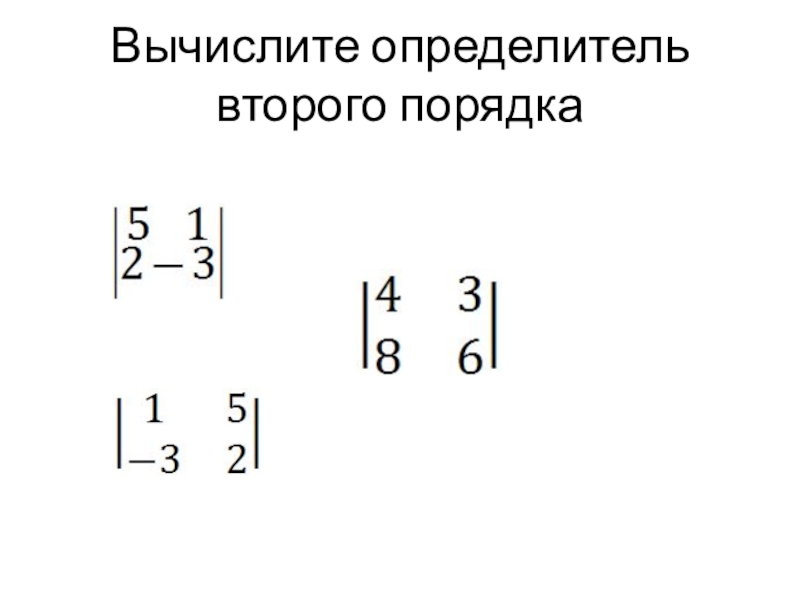
29. Вычислите определитель второго порядка
30. Определитель матрицы третьего порядкаОпределителем матрицы третьего порядка,
31. Определитель матрицы третьего порядкаОпределителем матрицы третьего порядка,
32. Определитель третьего порядка = a1b2c3+a3b1c2+a2b3c1-a3b2c1-a2b1c3-a1b3c2
33. = a1b2c3+a3b1c2+a2b3c1-a3b2c1-a2b1c3-a1b3c2=-48 =6⋅1⋅2+(-2) ⋅3⋅(-3)+4⋅(-3) ⋅0--(-2) ⋅1⋅0-4⋅3⋅2-6⋅(-3) ⋅(-3)Определитель третьего порядка
34. Определитель третьего порядка = a1b2c3+a3b1c2+a2b3c1-a3b2c1-a2b1c3-a1b3c2
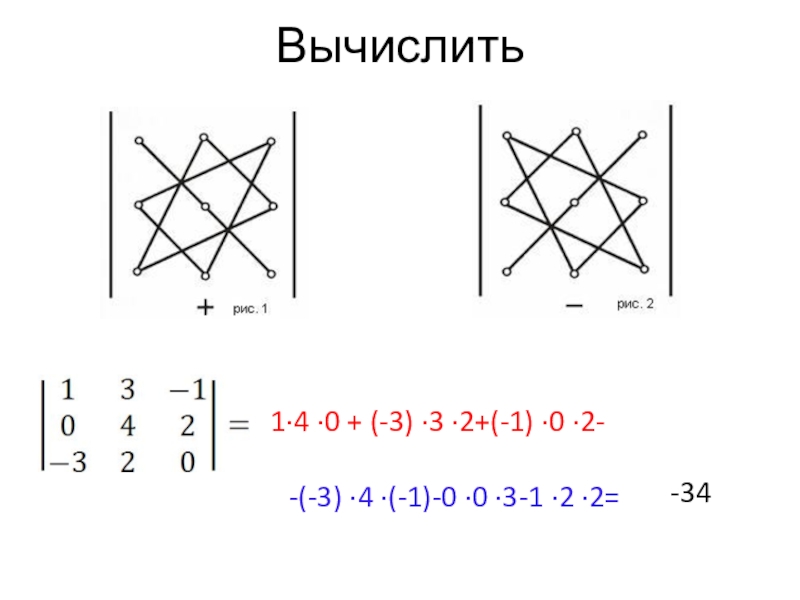
35. Вычислить 1∙4 ∙0 + (-3) ∙3 ∙2+(-1) ∙0 ∙2--(-3) ∙4 ∙(-1)-0 ∙0 ∙3-1 ∙2 ∙2=-34
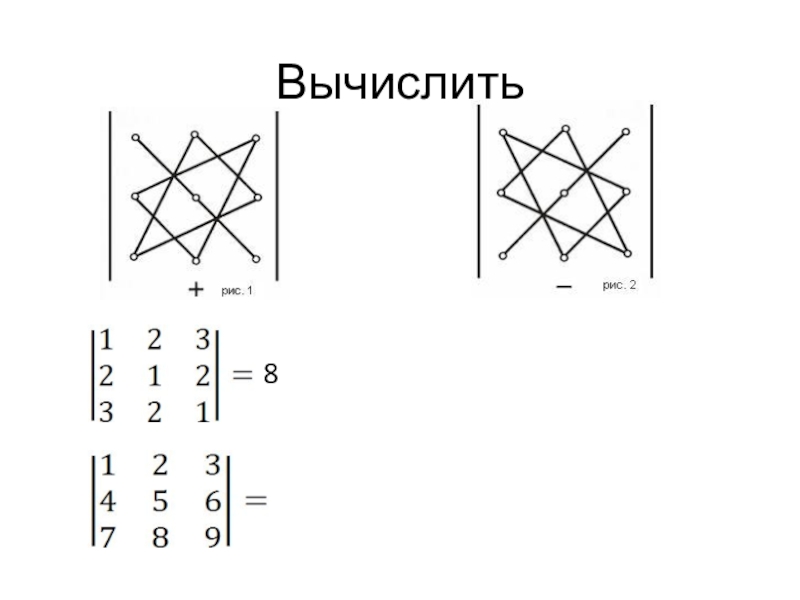
36. Вычислить 8
37. Решение систем линейных уравнений с тремя переменными
38. Решение систем уравнений с тремя переменными
39. Решение систем уравнений с тремя переменными
40. Решение систем уравнений с тремя переменными≠0
41. Решение систем уравнений с тремя переменными
42. Решение систем уравнений с тремя переменными
43. Решение систем уравнений с тремя переменными
44. Решение систем уравнений с тремя переменными
45. Решение систем уравнений с тремя переменными
46. Решение систем уравнений с тремя переменными
47. Решение систем уравнений с тремя переменными
48. Решение систем уравнений с тремя переменными
49. Решение систем уравнений с тремя переменными
50. Решение систем уравнений с тремя переменными
51. Решение систем уравнений с тремя переменными
52. Решение систем уравнений с тремя переменными
53. Решение систем уравнений с тремя переменными
54. Решение систем уравнений с тремя переменными
55. Решение систем уравнений с тремя переменными
56. Решение систем уравнений с тремя переменными
57. Решение систем уравнений с тремя переменными
58. Решение систем уравнений с тремя переменными
59. Решение систем уравнений с тремя переменными
60. Решение систем уравнений с тремя переменными
61. Решение систем уравнений с тремя переменными
62. Решение систем уравнений с тремя переменными
63. Решение систем уравнений с тремя переменнымиПроверка
64. Решение систем уравнений с тремя переменнымиПроверка
65. Решение систем уравнений с тремя переменнымиПроверка
66. Решение систем уравнений с тремя переменнымиПроверка
67. Решение систем уравнений с тремя переменнымиПроверка
68. Решение систем уравнений с тремя переменнымиПроверка
69. Решение систем уравнений с тремя переменнымиПроверка
70. Решение систем уравнений с тремя переменнымиПроверка
71. Решение систем уравнений с тремя переменнымиПроверка
72. Решение систем уравнений с тремя переменнымиПроверка

Системой уравнений с двумя переменными называется система вида: где а11, а12, а21, а22 – коэффициенты при переменных, в1, в2 – свободные членыРешением системы уравнений с двумя переменными называется пара чисел, являющихся

Главная
Математика
Презентация урока Решение системы линейных уравнений с тремя переменными

Слайд 1Решение системы линейных уравнений с двумя переменными.

Слайд 2 Системой уравнений с двумя переменными называется система вида: где а11, а12, а21,

а22 – коэффициенты при переменных, в1, в2 – свободные члены

Решением системы уравнений с двумя переменными называется пара чисел, являющихся решением каждого уравнения

Системой уравнений с двумя переменными называется система вида: где а11, а12, а21,

Слайд 3Методы решения системы уравнений
Метод подстановки;
Метод сложения;
Графический метод;
Метод Крамера

Слайд 4Метод Крамера

Слайд 5 Габриель Крамер
(нем. Gabriel Cramer, 31 июля 1704, Женева, Швейцария

— 4 января 1752, Баньоль-сюр-Сез, Франция) — швейцарский математик, ученик и друг Иоганна Бернулли, один из создателей линейной алгебры.

Габриель Крамер (нем. Gabriel Cramer, 31 июля 1704, Женева, Швейцария — 4 января 1752, Баньоль-сюр-Сез, Франция) —

Слайд 6Метод Крамера
Определение
Матрицей размеров mxn называется прямоугольная таблица чисел, содержащая m строк

и n столбцов. Числа, составляющие матрицу,
называются элементами матрицы.

Метод КрамераОпределениеМатрицей размеров mxn называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу,

Слайд 7Метод Крамера
Матрица

Слайд 8Метод Крамера
Матрица
Элементы a1 и b2 образуют главную диагональ
Элементы b1 и

a2образуют побочную диагональ

Слайд 9Определитель матрицы второго порядка
Определителем матрицы второго порядка , или определителем второго

порядка, называется число, равное разности произведения элементов главной и побочной диагоналей.

Определитель матрицы второго порядкаОпределителем матрицы второго порядка , или определителем второго порядка, называется число, равное разности произведения

Слайд 10Определитель матрицы

Слайд 11Определитель матрицы

Слайд 12Определитель матрицы

Слайд 13Свойства определителей:
Если в определителе какие-либо две строки (столбца) равны между собой,

то такой определитель равен 0.
Общий множитель всех элементов какой-либо строки (или столбца) можно выносить за знак определителя.
Если поменять в определителе местами какие-либо две строки (столбца), то определитель меняет знак.
Если все элементы какой-либо строки (столбца) определителя равны 0, то такой определитель равен 0.