- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока на тему : Параллельное проектирование и его свойства
Содержание
- 1. Презентация урока на тему : Параллельное проектирование и его свойства
- 2. II. АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ Учитель. В течение нескольких
- 3. Дидактическая игра «Правильно-неправильно» Проводим при помощи зеленых и
- 4. 3) Правильно ли, что если плоскость пересекает
- 5. III. МОТИВАЦИЯ УЧЕБНО -ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИПрием значимости Создаем установку
- 6. Будж аль Араш (Дубаи, ОАЭ) Дом-банкнота (Каунас, Литва)
- 7. Дом-рояль со скрипкой (Китай)
- 8. IV. СООБЩЕНИЕ ТЕМЫ, ФОРМУЛИРОВАНИЕ ЦЕЛИ УРОКАV. ВОСПРИЯТИЕ
- 9. Прием новизны Включаем в содержание учебного материала
- 10. Прием «Исследование» Учащиеся на основе изложенного учителем материала,
- 11. Исследование 1 При помощи проектора исследуем проекции таких
- 12. Слайд 12
- 13. Исследование 2 Исследуем проекции таких фигур: угол между
- 14. Слайд 14
- 15. Работа с учебникомКоллективное решение упражнений1. (№ 325)
- 16. VII.ДОМАШНЕЕ ЗАДАНИЕ Решить задачи:1. Треугольник А1В1С1 -
- 17. VIII.РЕФЛЕКСИЯ. ВЫСТАВЛЕНИЕ ОЦЕНОК ✔ Что нового
- 18. Я попрошу вас определить, какое высказывание из
- 19. IX. ДОМАШНЕЕ УДОВОЛЬСТВИЕ(Стратегия творческого поиска «Путь изсистемы»:
- 20. Дом-библиотека (Минск, Белоруссия)Ворота в Европу (Мадрид, Испания)Пирамида близ Лувра (Париж, Франция)
II. АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ Учитель. В течение нескольких уроков мы изучаем тему «Параллельные плоскости». Сегодня мы продолжим ее изучать, но чтобы наша работа была продуктивной, давайте вспомним некоторые свойства параллельных плоскостей.
Слайд 1Тема: Параллельное проектирование и его свойства Акмеологический урок геометрии
в 10 классе
Цель: сформулировать понятие параллельного проектирования; добиться усвоения свойств параллельного проектирования; формировать у учащихся умение применять понятия и свойства параллельного проектирования к решению задач; развивать абстрактное мышление, пространственное воображение и интуицию, познавательный интерес.
Тип урока: усвоение новых знаний
Технологии: стратегии творческого поиска: «Сбор грибов», «Поэзия», «Уникум», «Принцип дополняемости», «Путь из системы».
Приемы: значимости, новизны, исследования, дидактическая игра.
Оборудование: компьютер, мультимедийный проектор, модели плоских геометрических фигур.
Раздаточный материал: карточка-справочник, карточки красного и зеленого цветов.
Слайд 2 II. АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ
Учитель. В течение нескольких уроков мы изучаем тему
«Параллельные плоскости». Сегодня мы продолжим ее изучать, но чтобы наша работа была продуктивной, давайте вспомним некоторые свойства параллельных плоскостей.
Слайд 3 Дидактическая игра
«Правильно-неправильно»
Проводим при помощи зеленых и красных карточек. Вопросы проектируем
на экран. Потом освещаем ответ.
1) Правильно ли, что через произвольную точку в пространстве можно провести лишь одну прямую, параллельную данной прямой?
Ответ. Правильно. По теореме, через точку, которая не лежит на данной прямой, можно провести прямую, параллельную этой прямой, и только одну.
2) Правильно ли, что если две прямые в пространстве не пересекаются, то они параллельны?
Ответ. Неправильно. В пространстве не имеют общих точек параллельные и скрещивающиеся прямые.
1) Правильно ли, что через произвольную точку в пространстве можно провести лишь одну прямую, параллельную данной прямой?
Ответ. Правильно. По теореме, через точку, которая не лежит на данной прямой, можно провести прямую, параллельную этой прямой, и только одну.
2) Правильно ли, что если две прямые в пространстве не пересекаются, то они параллельны?
Ответ. Неправильно. В пространстве не имеют общих точек параллельные и скрещивающиеся прямые.
Слайд 4 3) Правильно ли, что если плоскость пересекает одну из двух параллельных
прямых, то она пересекает и вторую?
Ответ. Правильно. По теореме, если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая также пересекает эту плоскость.
4) Правильно ли, что если прямая параллельна некоторой плоскости, то в плоскости существует прямая, параллельная поданной прямой?
Ответ. Правильно. По доказанному ранее свойству, если прямая параллельна некоторой плоскости, то она параллельна какой-то прямой, которая относится к этой плоскости.
5) Правильно ли, что если две прямые параллельны поданной плоскости, то они параллельны друг другу?
Ответ. Неправильно. Эти прямые могут быть не только параллельными, но и пересекаться, а также могут быть скрещивающимися.
Ответ. Правильно. По теореме, если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая также пересекает эту плоскость.
4) Правильно ли, что если прямая параллельна некоторой плоскости, то в плоскости существует прямая, параллельная поданной прямой?
Ответ. Правильно. По доказанному ранее свойству, если прямая параллельна некоторой плоскости, то она параллельна какой-то прямой, которая относится к этой плоскости.
5) Правильно ли, что если две прямые параллельны поданной плоскости, то они параллельны друг другу?
Ответ. Неправильно. Эти прямые могут быть не только параллельными, но и пересекаться, а также могут быть скрещивающимися.
Слайд 5III. МОТИВАЦИЯ УЧЕБНО -ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ
Прием значимости
Создаем установку на необходимость изучать материал
в связи с его актуальностью в современном мире, эстетической ценностью.
Слайд 8
IV. СООБЩЕНИЕ ТЕМЫ, ФОРМУЛИРОВАНИЕ ЦЕЛИ УРОКА
V. ВОСПРИЯТИЕ И ОСОЗНАНИЕ УЧЕБНОГО МАТЕРИАЛА
Пусть
дано произвольную плоскость α и точку А
Не принадлежащую α. Проведем через точку А прямую, которая
пересекает плоскость α в точке А1. Полученную таким образом точку
А1 называют проекцией точки А на плоскость α , прямую АА1 –
проектирующей прямой, плоскость α - плоскостью проекции.
Чтобы построить проекцию произвольной фигуры, нужно
спроектировать на плоскость проекции каждую точку данной фигуры.
Если проектируемые прямые проводят через одну точку,
говорят о центральном проектировании (перспективе). Если
проектирование осуществляют параллельными прямыми, его
называют параллельным проектированием. В геометрии обычно
применяют параллельное проектирование.
Не принадлежащую α. Проведем через точку А прямую, которая
пересекает плоскость α в точке А1. Полученную таким образом точку
А1 называют проекцией точки А на плоскость α , прямую АА1 –
проектирующей прямой, плоскость α - плоскостью проекции.
Чтобы построить проекцию произвольной фигуры, нужно
спроектировать на плоскость проекции каждую точку данной фигуры.
Если проектируемые прямые проводят через одну точку,
говорят о центральном проектировании (перспективе). Если
проектирование осуществляют параллельными прямыми, его
называют параллельным проектированием. В геометрии обычно
применяют параллельное проектирование.
Слайд 9Прием новизны
Включаем в содержание учебного материала интересные сведения, факты, исторические данные.
Историческая
справка
ЖЕРАР ДЕЗАРГ (2 марта 1593 – 8 октября 1662). Французский математик. Был военным инженером. Заложил основы проективной и начертательной геометрии. В своих исследованиях систематически применял перспективное изображение. Первым ввел в геометрию бесконечно отдаленные элементы. В произведениях о резьбе по камню и о солнечных часах Дезарг дает геометрическое обоснование практических операций.
ГАСПАР МОНЖ (10 мая 1746 – 28 июня 1818). Французский математик и общественный деятель, член Парижской АН, профессор Мезьерской военно-инженерной школы. Создал общий метод изображения пространственных фигур на плоскости. Написал учебник «Начертательная геометрия», который был издан в 1799 году. Вместе с Наполеоном Бонапартом принимал участие в Египетской экспедиции. Во времена Первой империи Монж стал сенатором, получил титул графа. В период Реставрации был лишен всех прав и изгнан из Академии наук.
ЖЕРАР ДЕЗАРГ (2 марта 1593 – 8 октября 1662). Французский математик. Был военным инженером. Заложил основы проективной и начертательной геометрии. В своих исследованиях систематически применял перспективное изображение. Первым ввел в геометрию бесконечно отдаленные элементы. В произведениях о резьбе по камню и о солнечных часах Дезарг дает геометрическое обоснование практических операций.
ГАСПАР МОНЖ (10 мая 1746 – 28 июня 1818). Французский математик и общественный деятель, член Парижской АН, профессор Мезьерской военно-инженерной школы. Создал общий метод изображения пространственных фигур на плоскости. Написал учебник «Начертательная геометрия», который был издан в 1799 году. Вместе с Наполеоном Бонапартом принимал участие в Египетской экспедиции. Во времена Первой империи Монж стал сенатором, получил титул графа. В период Реставрации был лишен всех прав и изгнан из Академии наук.
Слайд 10Прием «Исследование»
Учащиеся на основе изложенного учителем материала, анализа литературы, решения познавательных
задач должны сформулировать вывод по поставленной проблеме.
Простейший природный пример параллельного проектирования – это тень, созданная солнечными лучами. А мы воспользуемся проектором и попробуем исследовать проекции некоторых фигур.
Простейший природный пример параллельного проектирования – это тень, созданная солнечными лучами. А мы воспользуемся проектором и попробуем исследовать проекции некоторых фигур.
Слайд 11Исследование 1
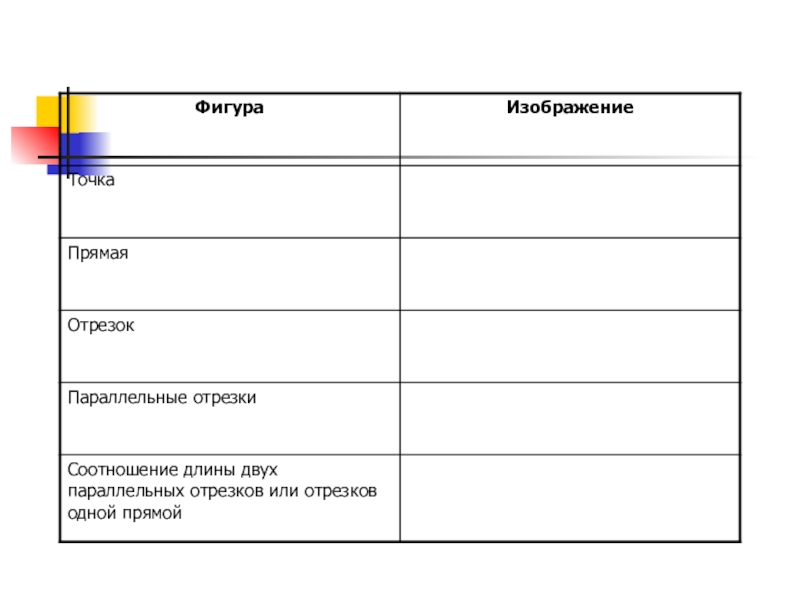
При помощи проектора исследуем проекции таких фигур: прямая, отрезок, параллельные
отрезки и их соотношение, соотношение отрезков одной прямой.
Результаты исследования учащиеся записывают в раздаточные карточки.
(Стратегия творческого поиска «Сбор грибов»: нужно отыскать множество данных, которые в сочетании обуславливают толчок к рождению вывода.)
Результаты исследования учащиеся записывают в раздаточные карточки.
(Стратегия творческого поиска «Сбор грибов»: нужно отыскать множество данных, которые в сочетании обуславливают толчок к рождению вывода.)
Слайд 13 Исследование 2
Исследуем проекции таких фигур: угол между прямыми, биссектриса угла, перпендикулярные
прямые, соотношение длины двух непараллельных отрезков.
Результаты исследования учащиеся записывают в раздаточные карточки (вставляют пропущенные слова).
(Стратегия творческого поиска «Поэзия»: используя ситуацию выбора в рамках возможного или доступного, применять возможности сочетания.)
Результаты исследования учащиеся записывают в раздаточные карточки (вставляют пропущенные слова).
(Стратегия творческого поиска «Поэзия»: используя ситуацию выбора в рамках возможного или доступного, применять возможности сочетания.)
Слайд 15
Работа с учебником
Коллективное решение упражнений
1. (№ 325) Проекция фигуры – точка.
Назовите эту фигуру.
2. (№ 328) Может ли быть:
а) ромб проекцией квадрата
б) ромб проекцией трапеции;
в) равнобокая трапеция проекцией неравнобокой;
г) неравнобокая трапеция проекцией равнобокой;
д) отрезок проекцией неплоской фигуры?
2. (№ 328) Может ли быть:
а) ромб проекцией квадрата
б) ромб проекцией трапеции;
в) равнобокая трапеция проекцией неравнобокой;
г) неравнобокая трапеция проекцией равнобокой;
д) отрезок проекцией неплоской фигуры?
VI. ФОРМИРОВАНИЕ УМЕНИЙ И НАВЫКОВ
(Стратегия эвристического творческого поиска
«Уникум»: предлагаем учащимся создать
качественно новый продукт творческой
деятельности, аналогов которому они не встречали).
Слайд 16 VII.ДОМАШНЕЕ ЗАДАНИЕ
Решить задачи:
1. Треугольник А1В1С1 - проекция
треугольника АВС. Постройте проекции
средних
линий и медиан треугольника АВС.
2. Нарисуйте произвольный
параллелограмм. Пусть он проекция ромба с углом
120о. Постройте проекцию высоты ромба,
проведенной из вершины этого угла
линий и медиан треугольника АВС.
2. Нарисуйте произвольный
параллелограмм. Пусть он проекция ромба с углом
120о. Постройте проекцию высоты ромба,
проведенной из вершины этого угла
Слайд 17
VIII.РЕФЛЕКСИЯ. ВЫСТАВЛЕНИЕ ОЦЕНОК
✔ Что нового вы узнали на уроке?
✔
Что изучили?
✔ Что повторили?
✔ К чему побуждает вас этот урок?
(Стратегия творческого поиска «Принцип дополняемости»: ищем объединяющую субстанциональную основу для разных точек зрения, осуществляем соответствующую коррекцию.)
✔ Что повторили?
✔ К чему побуждает вас этот урок?
(Стратегия творческого поиска «Принцип дополняемости»: ищем объединяющую субстанциональную основу для разных точек зрения, осуществляем соответствующую коррекцию.)
Слайд 18
Я попрошу вас определить, какое высказывание из записанных на доске может
быть эпиграфом к этому уроку, и записать его в тетрадь.
Геометрическое изображение играет огромную роль в исследовательской работе почти во всех разделах математики, даже наиболее ответственных
А. Колмогоров
Геометрия – посредник между природой и архитектурой
А. Картале
Архитектура величественных пирамидных храмов является молчащей математикой
О. Шпенглер
Геометрическое изображение играет огромную роль в исследовательской работе почти во всех разделах математики, даже наиболее ответственных
А. Колмогоров
Геометрия – посредник между природой и архитектурой
А. Картале
Архитектура величественных пирамидных храмов является молчащей математикой
О. Шпенглер
Слайд 19IX. ДОМАШНЕЕ УДОВОЛЬСТВИЕ
(Стратегия творческого поиска «Путь из
системы»: предлагаем индивидуальные
творческие задания, которые
стимулируют
личность к самовыявлению ее внутренней
сути, что даст возможность определить
направление ее дальнейшего развития.)
личность к самовыявлению ее внутренней
сути, что даст возможность определить
направление ее дальнейшего развития.)