- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Удивительный мир чисел
Содержание
- 1. Презентация Удивительный мир чисел
- 2. Цель: как можно больше отыскать удивительных натуральных чисел, установить их свойства и закономерности.
- 3. План1) Введение2) Фигурные числаЛинейные числа Плоские числа
- 4. Введение"Самые древние по происхождению числа – натуральные.
- 5. ВведениеПервое научное определение числа дал Эвклид в
- 6. Фигурные числа
- 7. Фигурные числаФигурные числа — общее название чисел,
- 8. Фигурные числа: линейныеЛинейные числа — числа, не
- 9. Фигурные числа: плоскиеПлоские числа — числа, представимые
- 10. Фигурные числа: телесныеТелесные числа — числа, представимые
- 11. Многоугольные числаВыкладывая различные правильные многоугольники, можно получить
- 12. Многоугольные числа: треугольныеПоследовательность треугольных чисел: 1, 3,
- 13. Многоугольные числа: квадратныеКвадратные числа представляют собой произведение
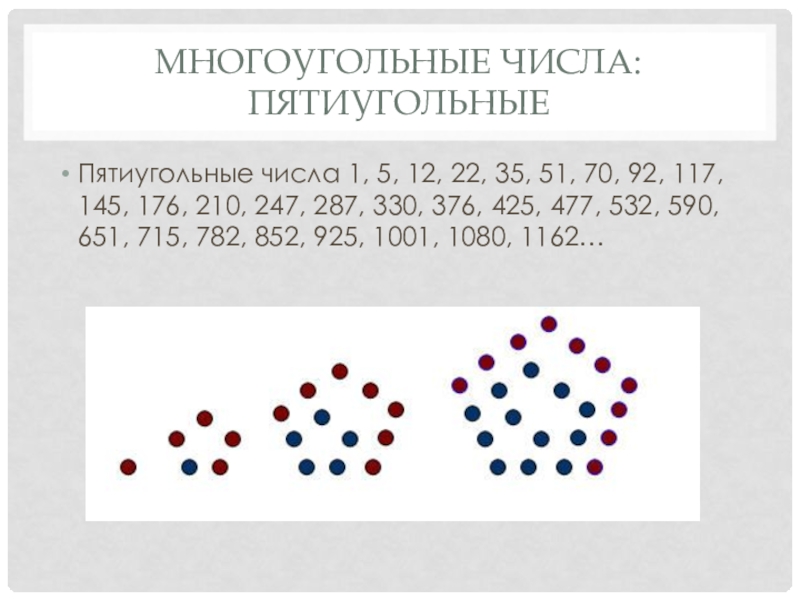
- 14. Многоугольные числа: пятиугольныеПятиугольные числа 1, 5, 12,
- 15. Многоугольные числа: пирамидальныеПирамидальные числа возникают при складывании
- 16. Дружественные числа
- 17. Дружественные числаДружественные числа – это два натуральных
- 18. Дружественные числаДолго считалось, что следующую пару дружественных
- 19. Совершенные числа
- 20. Совершенные числаСовершенное число— натуральное число, равное сумме
- 21. Совершенные числаСовершенные числа образуют последовательность.6,28,496,8128,33 550 336,8
- 22. Совершенные числаПримеры1-е совершенное число — 6 имеет
- 23. ЗаключениеВ труде, в учении, в игре, во
- 24. Спасибо за внимание
Цель: как можно больше отыскать удивительных натуральных чисел, установить их свойства и закономерности.
Слайд 1Выполнила ученица 6-В класса Такенова Алия
Учитель: Маткина Наталья Михайловна
Удивительный мир чисел
Слайд 2Цель: как можно больше отыскать удивительных натуральных чисел, установить их свойства
и закономерности.
Слайд 3План
1) Введение
2) Фигурные числа
Линейные числа
Плоские числа
Телесные числа
Многоугольные числа
Треугольные
числа
Квадратные числа
Пятиугольные числа
Пирамидальные числа
3)Дружественные числа
4)Совершенные числа
5)Заключение
Квадратные числа
Пятиугольные числа
Пирамидальные числа
3)Дружественные числа
4)Совершенные числа
5)Заключение
Слайд 4Введение
"Самые древние по происхождению числа – натуральные. "Ручейки" натуральных чисел, сливаясь,
порождают безбрежный океан вещественных и разного рода особых специальных чисел", так писал о числах Б.А.Кордемский в своей книге "Удивительный мир чисел". Если покопаться в огромном массиве чисел, которых больше, чем руды в земле, можно найти свойства интересные и удивительные, диковинные и забавные, неожиданные и курьёзные. Можно встретить числа – уникумы, похожих на которые нет среди остальных чисел, а также целые букеты чисел, образующих красивые сочетания.
Слайд 5Введение
Первое научное определение числа дал Эвклид в своих "Началах": "Единица есть
то, в соответствии, с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц". Так определял понятие числа и русский математик Магницкий в своей "Арифметике" (1703 г.). Первоначальные представления о числе появились в эпоху каменного века, при переходе от простого собирания пищи к ее активному производству, примерно 100 веков до н. э. Числовые термины тяжело зарождались и медленно входили в употребление. Древнему человеку было далеко до абстрактного мышления, хватило того, что он придумал числа: "один" и "два". Остальные количества для него оставались неопределенными и объединялись в понятии "много".
Слайд 7Фигурные числа
Фигурные числа — общее название чисел, связанных с той или
иной геометрической фигурой. Различают следующие виды фигурных чисел:
Слайд 8Фигурные числа: линейные
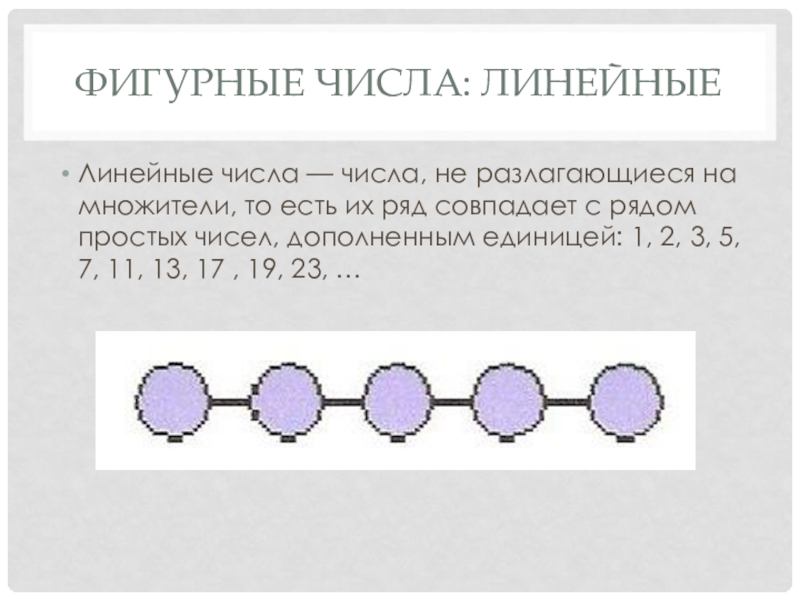
Линейные числа — числа, не разлагающиеся на множители, то
есть их ряд совпадает с рядом простых чисел, дополненным единицей: 1, 2, 3, 5, 7, 11, 13, 17 , 19, 23, …
Слайд 9Фигурные числа: плоские
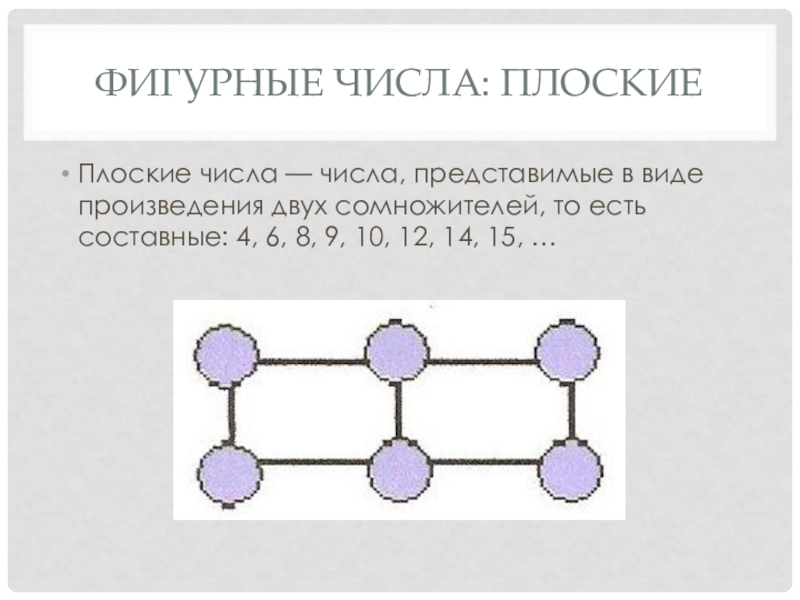
Плоские числа — числа, представимые в виде произведения двух
сомножителей, то есть составные: 4, 6, 8, 9, 10, 12, 14, 15, …
Слайд 10Фигурные числа: телесные
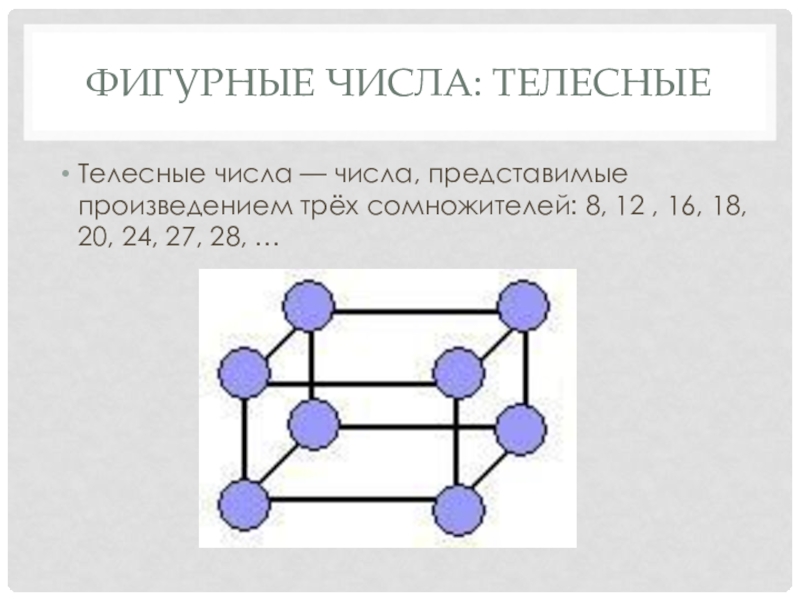
Телесные числа — числа, представимые произведением трёх сомножителей: 8,
12 , 16, 18, 20, 24, 27, 28, …
Слайд 11Многоугольные числа
Выкладывая различные правильные многоугольники, можно получить разные классы многоугольных чисел.
Предположительно от фигурных чисел возникло выражение: "Возвести число в квадрат или в куб".
Слайд 12Многоугольные числа: треугольные
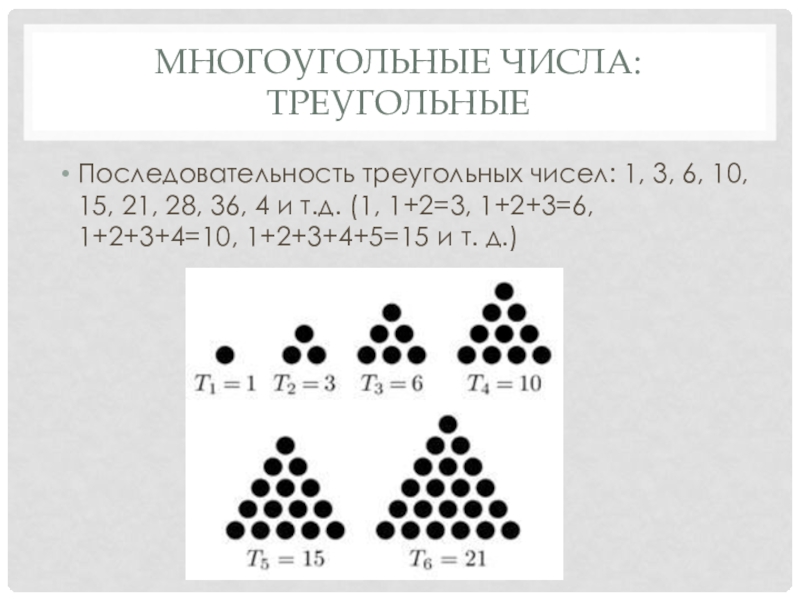
Последовательность треугольных чисел: 1, 3, 6, 10, 15, 21,
28, 36, 4 и т.д. (1, 1+2=3, 1+2+3=6, 1+2+3+4=10, 1+2+3+4+5=15 и т. д.)
Слайд 13Многоугольные числа: квадратные
Квадратные числа представляют собой произведение двух одинаковых натуральных чисел,
то есть являются полными квадратами: 1, 4, 9, 16, 25, 36, и т.д. (1+3=4, 1+3+5=9, 1+3+5+7=16).
Слайд 14Многоугольные числа: пятиугольные
Пятиугольные числа 1, 5, 12, 22, 35, 51, 70,
92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001, 1080, 1162…
Слайд 15Многоугольные числа: пирамидальные
Пирамидальные числа возникают при складывании круглых камушков горкой так,
чтобы они не раскатывались. Получается пирамида. Каждый слой в такой пирамиде - треугольное число. Наверху один камушек, под ним - 3, под теми - 6 и т.д.: 1, 1+3=4, 1+3+6=10, 1+3+6+10=20, ... Кубические числа возникают при складывании кубиков: 1, 2·2·2=8, 3·3·3=27, 4·4·4=64, 5·5·5=125...
Слайд 17Дружественные числа
Дружественные числа – это два натуральных числа, для которых сумма
всех делителей первого числа (кроме него самого) равна второму числу и сумма всех делителей второго числа (кроме него самого) равна первому числу. История дружественных чисел теряется в глубине веков. Эти удивительные числа были открыты последователями Пифагора. Правда пифагорейцы знали только одну пару дружественных чисел – 220 и 284. Проверим эту пару чисел на свойство дружественных чисел: 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284, 1 + 2 + 4 + 71 + 142 = 220 .
Слайд 18Дружественные числа
Долго считалось, что следующую пару дружественных чисел 17296 и 18416
открыл в 1636 году знаменитый французский математик Пьер Ферма. Но недавно в одном из трактатов арабского ученого Ибн аль-Банны (1256-1321) были найдены строки "Числа 17296 и 18416 являются дружественными. Аллах всеведущ". Пару чисел 220 и 284 стали считать символом дружбы. В Средние века имели хождение талисманы с выгравированными на них числами 220 и 284, якобы способствующими укреплению любви.
Слайд 20Совершенные числа
Совершенное число— натуральное число, равное сумме всех своих собственных делителей
(то есть всех положительных делителей, отличных от самого́ числа). По мере того как натуральные числа возрастают, совершенные числа встречаются всё реже. Неизвестно, бесконечно ли множество всех совершенных чисел.
Слайд 21Совершенные числа
Совершенные числа образуют последовательность.
6,
28,
496,
8128,
33 550 336,
8 589 869 056,
137 438
691 328,
2 305 843 008 139 952 128,
2 658 455 991 569 831 744 654 692 615 953 842 176,
191 561 942 608 236 107 294 793 378 084 303 638 130 997 321 548 169 216, …
2 305 843 008 139 952 128,
2 658 455 991 569 831 744 654 692 615 953 842 176,
191 561 942 608 236 107 294 793 378 084 303 638 130 997 321 548 169 216, …
Слайд 22Совершенные числа
Примеры
1-е совершенное число — 6 имеет следующие собственные делители: 1,
2, 3; их сумма равна 6.
2-е совершенное число — 28 имеет следующие собственные делители: 1, 2, 4, 7, 14; их сумма равна 28.
3-е совершенное число — 496 имеет следующие собственные делители: 1, 2, 4, 8, 16, 31, 62, 124, 248; их сумма равна 496.
4-е совершенное число — 8128 имеет следующие собственные делители: 1, 2, 4, 8, 16, 32, 64, 127, 254, 508, 1016, 2032, 4064; их сумма равна 8128.
2-е совершенное число — 28 имеет следующие собственные делители: 1, 2, 4, 7, 14; их сумма равна 28.
3-е совершенное число — 496 имеет следующие собственные делители: 1, 2, 4, 8, 16, 31, 62, 124, 248; их сумма равна 496.
4-е совершенное число — 8128 имеет следующие собственные делители: 1, 2, 4, 8, 16, 32, 64, 127, 254, 508, 1016, 2032, 4064; их сумма равна 8128.
Слайд 23Заключение
В труде, в учении, в игре, во всякой творческой деятельности нужны
человеку сообразительность, находчивость, догадка, умение рассуждать – всё то, что наш народ определяет одним словом «смекалка». Смекалку можно воспитывать и развивать систематическими и постепенными упражнениями, в частности решением математических задач как школьного курса, так и задач, возникающих из практики, связанных с наблюдениями окружающего нас мира вещей и событий. Мир полон тайн и загадок. Но разгадать их могут только пытливые. Современная наука встречается с величинами такой сложной природы, что для их изучения приходится изобретать все новые виды чисел. И нам бы хотелось продолжить изучать эти числа, их свойства, закономерности…. Он такой удивительный МИР чисел!