Разработано учителем математики гимназии №22 Захарьян А. А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад темы Решение задач с параметрами в итоговом повторении курса алгебры.
Содержание
- 1. Презентация темы Решение задач с параметрами в итоговом повторении курса алгебры.
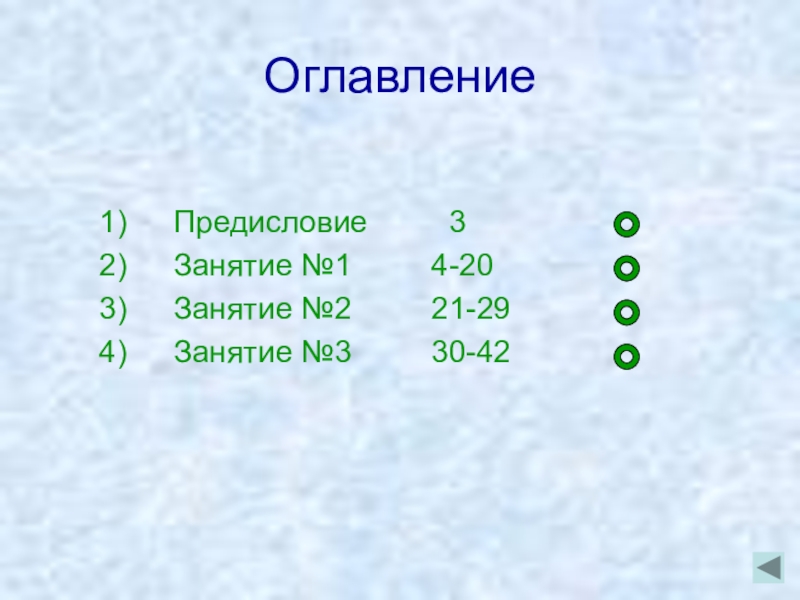
- 2. Оглавление Предисловие 3 Занятие №1 4-20 Занятие №2 21-29 Занятие №3 30-42
- 3. ПредисловиеВ последнее время в билетах вступительных экзаменов
- 4. Занятие №1 (2 часа)Главное, что должен усвоить
- 5. Пример №1. Сравнить –а и 5а Решение:1)
- 6. Пример №2. Решить уравнение ах=2Решение:1) если а=0,
- 7. Пример №3 Решить уравнение (а2-9)х=а+3 Решение:1)
- 8. Пример №4 Решить неравенство: ах0, то2) если а0, то х
- 9. Пример №5 Решить уравнение Решение:Ответ: если
- 10. Пример №6 Решить уравнение Решение:1) если
- 11. Пример №7 Решить уравнение Решение:Ответ: если b-4, то x=b.
- 12. Пример №8 Решить уравнение Решение:1) если
- 13. Пример №9 Решить неравенство Решение: 1)
- 14. a)
- 15. б) учитывая, что при то Ответ: если
- 16. если
- 17. Пример №10 При каких а уравнение
- 18. Пример №11 При каких а уравнение
- 19. Задачи для самостоятельного домашнего решения задаются с
- 20. б) (при а=-2 решений нет; при
- 21. Занятие №2 (2 часа)Урок начинается с разбора домашнего задания. Затем учитель предлагает решить более общую задачу.
- 22. Пример №12 Выяснить, при каких значениях параметра
- 23. Решение:1) уравнение имеет два различных корня тогда
- 24. 3) уравнение имеет два корня
- 25. Самостоятельная работа. Вариант I1. Для всякого а
- 26. 1) если b=12, то 2) если b=-12,
- 27. 3. Для каждого значения параметра решить неравенство:Решение:
- 28. 2) -2
- 29. Вариант IIЗадания аналогичны заданиям варианта I.1. Ответ:
- 30. Занятие №3 (2 часа)Теперь можно приступать к решению задач ЕГЭ с параметрами.
- 31. Пример №1. Найти все значения параметра p,
- 32. f ’(a)=0 Т.к.
- 33. Пример №2. Найти все значения а, при
- 34. 1) если 0
- 35. 2) если а>1, то Чтобы решение удовлетворяло условию задачи, необходимо и достаточно, чтобы Ответ:
- 36. Пример №3. Найти все значения параметра а,
- 37. Решим неравенство методом интервалов, рассмотрев функцию
- 38. т.е. 3) если - аналогично случаю 1) Ответ: 0 4 a
- 39. Пример №4. Найти все значения параметра p,
- 40. Рассмотрим функцию D(f)=[0; ),f(t)=0
- 41. 2) Узнаем при каких p уравнениеимеет ровно
- 42. Но уравнению
Слайд 1 Презентация темы «Решение задач с параметрами в итоговом повторении курса
Слайд 3Предисловие
В последнее время в билетах вступительных экзаменов по математике, в ЕГЭ
В классах с углублённым изучением математики параметрам уделяется достаточно внимания, начиная с решения линейных уравнений. При изучении каждой темы «углублёнки» можно найти время для решения задач с параметрами. Чего нельзя сказать об общеобразовательных классах и классах с гуманитарным уклоном. Поэтому я предлагаю учителям, работающим в неспециализированных выпускных классах перед итоговым повторением уделить несколько часов решению задач с параметрами
Слайд 4Занятие №1 (2 часа)
Главное, что должен усвоить школьник это то, что
Задачи надо начинать решать с очень простых, постепенно усложняя их.
Слайд 5Пример №1. Сравнить –а и 5а
Решение:
1) если а
2) если а=0, то –а=0, 5а=0, значит –а=5а
3) если а>0, то –а<0, 5a>0, значит –а<5a.
Ответ: если a<0, то –а>5a
если а=0, то–а=5а
если а>0, то–а<5a.
a
a<0
a=0
a>0
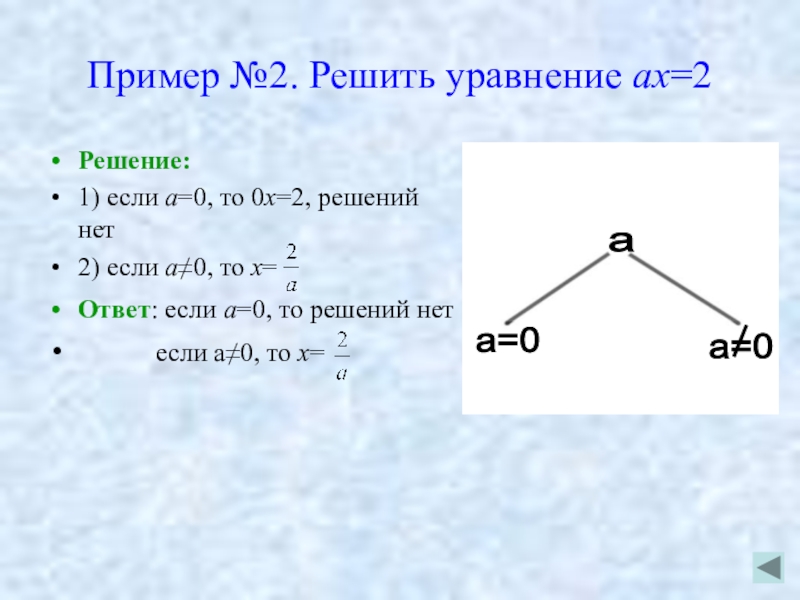
Слайд 6Пример №2. Решить уравнение ах=2
Решение:
1) если а=0, то 0х=2, решений нет
2) если а≠0, то х=
Ответ: если а=0, то решений нет
если а≠0, то х=
a
a=0
a=0
Слайд 7Пример №3 Решить уравнение
(а2-9)х=а+3
Решение:
1) если а=3, то 0х=6, решений
2) если а=-3, то 0х=0, х
3) если а≠±3, то а2-9≠0,
Ответ: если а=3, то решений нет
если а=-3, то x
если а≠±3, то
a
a=3
a=-3
a=3
a=-3
Слайд 8Пример №4 Решить неравенство: ах0, то
2) если а
3) если а=0, то - «И»
Ответ: если а>0, то х<
если а<0, то
если а=0, то
a
a=0
a>0
a<0
Слайд 10Пример №6 Решить уравнение
Решение:
1) если а=-1, то -2х+1+1=0; х=1
2) если
Ответ: если а=-1, то х=1
если а≠-1,то х=1 или
Слайд 12Пример №8 Решить уравнение
Решение:
1) если а≠0, то х=1
2) если а=0,
Ответ: если а≠0, то х=1
если а=0, то х=±1
Слайд 13Пример №9 Решить неравенство
Решение:
1) a) если b=1, то
2) если b≠±1, то неравенство квадратное
Слайд 16если
если то
Рассмотренные выше задачи требовалось просто решить. В следующих задачах будет поставлено какое-то более «узкое», конкретное условие.
Слайд 17Пример №10 При каких а уравнение
имеет единственное решение?
Решение:
1) если
2) если а≠0, то уравнение квадратное и оно имеет единственное решение при D=0
D=1-12a
Ответ: при а=0 или а=
Слайд 18Пример №11 При каких а уравнение
имеет единственное решение?
Решение:
1) если а=2,
2) если а≠2, то уравнение имеет единственное решение при D=0
Ответ: при а=5
Слайд 19Задачи для самостоятельного домашнего решения задаются с ответами для самоконтроля
При
при
2) Решить уравнение:
a)
(при а=1 или а=3 решений нет; при а≠1 и а≠3 х=а)
Слайд 20б)
(при а=-2 решений нет; при а≠-2 х=2)
3)
(при )
Слайд 21Занятие №2 (2 часа)
Урок начинается с разбора домашнего задания. Затем учитель
Слайд 22Пример №12 Выяснить, при каких значениях параметра а уравнение
1) два различных корня;
2) не более одного корня;
3) два корня различных знаков;
4) два положительных корня.
Слайд 23Решение:
1) уравнение имеет два различных корня тогда и только тогда, когда
2) а) если а=4, то
б)
Слайд 243) уравнение имеет два корня различных
знаков тогда и
4) уравнение имеет два положительных корня тогда и только тогда, когда
Слайд 25Самостоятельная работа.
Вариант I
1. Для всякого а решить уравнение
Решение:
Т.к. сумма коэффициентов равна
Ответ: 1; 2а.
2. При каких b уравнение имеет единственный корень? Для каждого b найти этот корень.
Решение:
Квадратное уравнение имеет единственный корень тогда и только тогда, когда D=0
Слайд 273. Для каждого значения параметра решить неравенство:
Решение:
Решим неравенство методом интервалов,
непрерывную на R, имеющую нули 2, -2, b
Рассмотрим три случая:
1)
b
-2
2
Слайд 29Вариант II
Задания аналогичны заданиям варианта I.
1.
Ответ: -1; 3а.
2.
Ответ: при b=20
при b=-20 x=2.
3.
Ответ: если то
если -1
Слайд 31Пример №1. Найти все значения параметра p, при которых уравнение
Решение:
Рассмотрим функцию f(a)= определённую на [-1;0)U(0;1] и найдём её область значений.
f(-1)=11; f(1)=3; при
f ’(a)=
Слайд 32f ’(a)=0
Т.к.
Чтобы уравнение а значит и данное уравнение имело хотя бы один корень, необходимо и достаточно, чтобы
Ответ:
Слайд 33Пример №2. Найти все значения а, при которых область определения функции содержит
Решение:
D(y):
Решим первое неравенство системы:
Слайд 352) если а>1, то
Чтобы решение удовлетворяло условию задачи, необходимо и
Ответ:
Слайд 36Пример №3. Найти все значения параметра а, при каждом из которых
Решение:
Слайд 37Решим неравенство методом интервалов, рассмотрев функцию
1) если
- решение содержит отрезок длиной 3, что не удовлетворяет условию задачи.
2) если 0
Чтобы решение удовлетворяло условию задачи, необходимо и достаточно, чтобы выполнялись условия:
a
0
4
4
a
0
Слайд 39Пример №4. Найти все значения параметра p, при которых уравнение имеет
Решение:
1)
Пусть =t, тогда
Слайд 40
Рассмотрим функцию
D(f)=[0; ),
f(t)=0
E(f)=(- ;0]
f’(t)= f’(t)<0
Значит графики функций и y=p могут иметь только одну общую точку, т.е. уравнение
а значит и уравнение
может иметь ровно один корень при
Слайд 412) Узнаем при каких p уравнение
имеет ровно один корень:
а) если 2p+3=0
б) если то уравнение имеет единственный корень при D=0.
D=0
Итак, уравнение имеет ровно
один корень при
Слайд 42Но уравнению
т.е. при и p=-1 уравнения и
имеют равное число корней, а именно, по одному.
Ответ: ; -1