информатики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Создание проблемных ситуаций на уроках математики
Содержание
- 1. Презентация Создание проблемных ситуаций на уроках математики
- 2. «Каждый человек видит тем больше нерешённых проблем,
- 3. Создание проблемных ситуаций через умышленно допущенные учителем
- 4. Создание проблемных ситуаций через использование занимательных заданий«Линейная
- 5. «Формулы сокращённого умножения»Преступники украли в банке большую
- 6. «Сумма n-первых членов арифметической прогрессии»“Примерно 200 лет
- 7. Создание проблемных ситуаций через решение
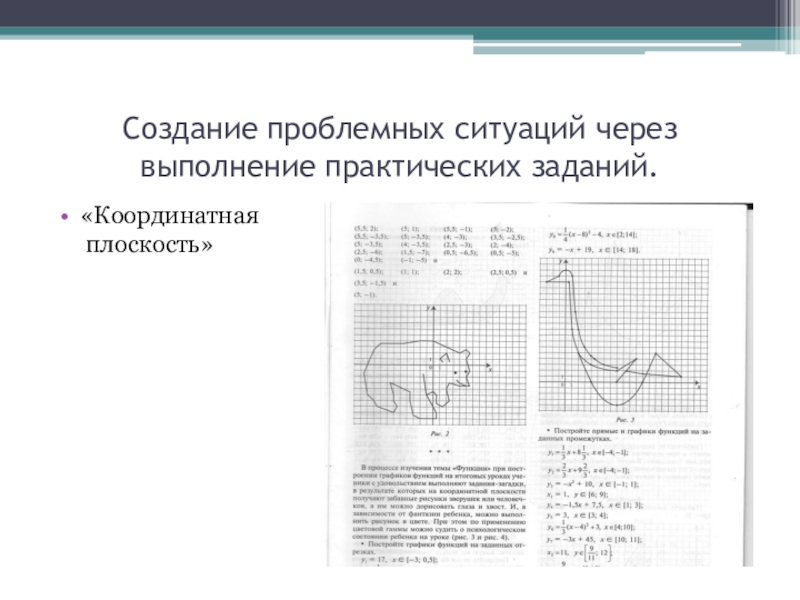
- 8. Создание проблемных ситуаций через выполнение практических заданий.«Координатная плоскость»
- 9. Создание проблемных ситуаций через решение задач на внимание и сравнение.
- 10. Создание проблемных ситуаций через противоречие нового материала
- 11. Создание проблемных ситуаций через различные способы решения
- 12. Создание проблемных ситуаций через выполнение небольших исследовательских
- 13. Рекомендации учителям по созданию проблемных ситуаций на
«Каждый человек видит тем больше нерешённых проблем, чем обширнее круг его знаний». С.Л.Рубинштейн Как же создавать проблемные ситуации?
Слайд 1Создание проблемных ситуаций
на уроках математики
Составитель: В.Г. Глазунова,
учитель математики и
Слайд 2«Каждый человек видит тем больше нерешённых проблем, чем обширнее круг его
знаний».
С.Л.Рубинштейн
Как же создавать проблемные ситуации?
Слайд 3Создание проблемных ситуаций через умышленно допущенные учителем ошибки
«Линейные уравнения с одной
переменной»
(3Х + 7) х 2 – 3 = 17
6Х + 14 – 3 = 17
6Х = 17 – 14 – 3
6Х = 0 Х = 0 При проверке ответ не сходится.
«Обманные задачи»: 1. Постройте прямоугольник со сторонами 2, 3 и 5 см. 2. Больший угол треугольника равен 50°. Найдите остальные углы. 3. Две стороны треугольника перпендикулярны третьей. Определите вид треугольника.
“У меня не получается”
6Х + 14 – 3 = 17
6Х = 17 – 14 – 3
6Х = 0 Х = 0 При проверке ответ не сходится.
«Обманные задачи»: 1. Постройте прямоугольник со сторонами 2, 3 и 5 см. 2. Больший угол треугольника равен 50°. Найдите остальные углы. 3. Две стороны треугольника перпендикулярны третьей. Определите вид треугольника.
“У меня не получается”
Слайд 4Создание проблемных ситуаций через использование занимательных заданий
«Линейная функция»
Обычная форма задания:
функция
задана формулой У = Х + 5
найдите значение функции при Х = 0, 7, -5, 1.
Занимательная форма задания: “угадать” формулу, записанную на карточке
найдите значение функции при Х = 0, 7, -5, 1.
Занимательная форма задания: “угадать” формулу, записанную на карточке
Слайд 5«Формулы сокращённого умножения»
Преступники украли в банке большую сумму денег.
Их поймали,
но похищенную сумму установить не удалось. Преступники категорически отказываются назвать её, утверждая, что записали это число в виде степени и зашифровали не только основание, но и её показатель.
Экспертам удалось узнать основание степени. Это число 597.
Но каким был показатель не говорят. После очередного допроса преступники сказали, что показатель степени является корнем уравнения
( 2y +1)2 – 4y2 =9
y = 2
5972 = (600 – 3)2 =6002 -2 х 600 х 3 + 32 = 360000 – 3600 + 9 =356409
Экспертам удалось узнать основание степени. Это число 597.
Но каким был показатель не говорят. После очередного допроса преступники сказали, что показатель степени является корнем уравнения
( 2y +1)2 – 4y2 =9
y = 2
5972 = (600 – 3)2 =6002 -2 х 600 х 3 + 32 = 360000 – 3600 + 9 =356409
Слайд 6«Сумма n-первых членов арифметической прогрессии»
“Примерно 200 лет тому назад в одной
из школ Германии на уроке математики учитель предложил ученикам найти сумму первых 100 натуральных чисел. Все принялись подряд складывать числа, а один ученик почти сразу же дал правильный ответ. Имя этого ученика Карл Фридрих Гаусс. В последствии он стал великим математиком. Как удалось Гауссу так быстро подсчитать эту сумму?”
Проблемная ситуация: как найти быстро сумму первых 100 натуральных чисел?
Решение проблемы (1 + 100) х 50 = 5050
Слайд 7 Создание проблемных ситуаций
через решение задач, связанных с жизнью.
«Периметр прямоугольника»
Семья Димы летом переехала в новый дом. Им отвели земельный участок прямоугольной формы. Папа решил поставить изгородь. Он попросил Диму сосчитать сколько потребуется штакетника, для изгороди, если на 1 погонный м. изгороди требуется 10 штук? Сколько денег потратит семья, если каждый десяток стоит 50 рублей.
«Площадь прямоугольника»
«Проценты»
«Площадь прямоугольника»
«Проценты»
Слайд 10Создание проблемных ситуаций через противоречие нового материала старому,
уже известному.
Вычисляем
(2 х 5)²= 2² х5² = 100
(3 х 4)²= 3² х 4² = 9 х 16 = 144
(5 : 6)² = 5² : 6² = 25 : 36
(3 + 4)² = 3² + 4² = 9 + 16 = 25
Попробуйте сосчитать по-другому.
( 3 + 4)² =7² = 49
(3 х 4)²= 3² х 4² = 9 х 16 = 144
(5 : 6)² = 5² : 6² = 25 : 36
(3 + 4)² = 3² + 4² = 9 + 16 = 25
Попробуйте сосчитать по-другому.
( 3 + 4)² =7² = 49
Слайд 11Создание проблемных ситуаций через различные способы решения одной задачи.
8 класс. Тема:
«Площадь трапеции»
а) провести диагональ и найти площадь трапеции как сумму площадей двух треугольников;
б) провести две высоты и найти площадь трапеции как сумму площадей прямоугольника и двух прямоугольных треугольников;
в) провести прямую, параллельную боковой стороне трапеции и найти площадь трапеции как сумму площадей параллелограмма и треугольника.
Слайд 12Создание проблемных ситуаций через выполнение небольших исследовательских заданий.
5 кл. Тема «Длина
окружности»
8 кл. «Квадратные уравнения»
Измерение на местности
8 кл. «Квадратные уравнения»
Измерение на местности
Слайд 13Рекомендации учителям по созданию проблемных ситуаций на уроке.
Подводить к противоречию с
уже известным и предлагать самим находить способ разрешения.
Побуждать делать сравнения, обобщения, выводы.
Создавать ситуации включения, используя задания, связанные с их жизненным опытом.
Использовать задачи с заведомо допущенными ошибками.
Предлагать практические исследовательские задания.
Отыскивать различные способы решения одной и той же задачи.
Излагать различные точки зрения на один и тот же вопрос.
Учить составлять задачи по статистическим данным своего населённого пункта.
Побуждать делать сравнения, обобщения, выводы.
Создавать ситуации включения, используя задания, связанные с их жизненным опытом.
Использовать задачи с заведомо допущенными ошибками.
Предлагать практические исследовательские задания.
Отыскивать различные способы решения одной и той же задачи.
Излагать различные точки зрения на один и тот же вопрос.
Учить составлять задачи по статистическим данным своего населённого пункта.