- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад проекта по математике В поисках оптимальных решений
Содержание
- 1. Презентация проекта по математике В поисках оптимальных решений
- 2. «Математика знает весьма тонкие изобретения, могущие принести
- 3. Легенда об основании Карфагена гласит,
- 4. ВведениеВеликий русский математик
- 5. Но не только людям приходится решать такие
- 6. Решение
- 7. Цели и задачи проекта:Показать историческую важность открытия
- 8. Из истории…Математикам удалось разработать методы решения задач
- 9. Слайд 9
- 10. Из истории…. В случае большого количества аргументов
- 11. Слайд 11
- 12. История одной задачи
- 13. История одной задачиПозднее Лейбниц высказал в одной
- 14. Из истории… Много задач на нахождение кривых
- 15. Открытие геодезических линий позволило продвинуться вперед картографам и геодезистам.
- 16. Из истории… Общий метод решения задач на
- 17. Слайд 17
- 18. Эксперимент
- 19. Эксперимент
- 20. Сказка
- 21. Задача Дидоны Найти прямоугольник наибольшей площади,
- 22. Торопящийся луч света Законы отражения и преломления
- 23. Этот принцип дает ключ к разгадке головоломки
- 24. Задача о трех железных дорогах
- 25. Лиса и курятник Нора
- 26. Задача о крокодилах В круглом озере живут
- 27. Та же задача для четырех крокодилов
- 28. Задача о кошке У мышки три выхода
- 29. Как провести шоссе? Из приречного города
- 30. Канал и плот Канал имеет
- 31. Бумажный змейЗмею, имеющему вид кругового сектора, желают
- 32. Слайд 32
- 33. Сколько решений имеет система:
- 34. Занимательные задачи Волшебный замок В
- 35. Занимательные задачи Найди число Найди наименьшее
- 36. Занимательные задачи
- 37. ЗаключениеНам удалось найти фигуру, имеющую наибольшую площадь
- 38. Слайд 38
Слайд 1В поисках оптимальных решений
9 «В» класс
Руководитель: Князева В.А.
МОУ СОШ №72
Станица Кривянская
2009г.
Слайд 2«Математика знает весьма тонкие изобретения, могущие принести большую пользу для удовлетворения
Декарт
Слайд 3 Легенда об основании Карфагена гласит, что когда финикийский корабль
Проблема:
Какая, известная геометрическая фигура имеет наибольшую площадь при заданном периметре?
Руины Карфагена
Слайд 4Введение
Великий русский математик П. Л. Чебышев в
Слайд 5Но не только людям приходится решать такие задачи.
Слайд 6 Решение проблемы будем искать
История разработки методов решения задач на экстремумы.
Решить проблему экспериментально.
Доказать гипотезу теоретически.
Слайд 7Цели и задачи проекта:
Показать историческую важность открытия методов решения задач на
В интересной и занимательной форме донести до учащихся тему проекта, используя дополнительную литературу, свои задумки и электронную презентацию.
Решить задачу Дидоны.
Слайд 8Из истории…
Математикам удалось разработать методы решения задач на наибольшие и наименьшие
Чем больше аргументов, тем сложнее задача, тем труднее выбрать оптимальные значения величин.
Для функций одного аргумента отыскание экстремумов делается с помощью дифференциального исчисления.
Даже старшеклассник справляется с задачей, если функция зависит от одного аргумента.
Но часто приходится отыскивать экстремумы функций многих переменных.
Слайд 9
Инженеры-технологи стремятся так организовать производство, чтобы на имеющемся станочном парке сделать как можно больше продукции.
Конструкторы ломают голову, стремясь изобрести наилегчайший прибор на космическом корабле.
Экономисты стараются так спланировать прикрепление заводов к источникам сырья, чтобы транспортные расходы оказались наименьшими.
Слайд 10Из истории…
. В случае большого количества аргументов для решения задачи требуется
Для решения таких задач составляются специальные программы, откуда и возникло название «линейное программирование». Задачи на линейное программирование впервые решил советский ученый Л. В. Канторович.
Линейное программирование сейчас применяется в самых различных областях.
Слайд 11 «Многие идеи
Янош Бояйи
История одной задачи
Слайд 12История одной задачи
Возникает задача: найти такую кривую, что двигаясь по ней, падающая точка А быстрее всего попадет в точку В. В 1696 году Иоганн Бернулли доказал, что искомой кривой является циклоида.
Иоганн Бернулли предложил Лейбницу найти решение (тот быстро нашел ответ), а Лейбниц предложил опубликовать «столь замечательную и до сих пор неслыханную задачу» для состязания между геометрами с годичным срок для решения
Слайд 13История одной задачи
Позднее Лейбниц высказал в одной заметке мнение, что во
Прогноз оказался верным – поступило лишь три решения, одно из которых принадлежало Лопиталю, второе – Якобу Бернулли, а третье было без подписи опубликовано в английском журнале. Но Иоганн Бернулли сразу угадал, что в Англии мог решить задачу с таким блеском только Исаак Ньютон.
Как писал сам Бернулли, он узнал Ньютона, как льва узнают по когтям.
И действительно, задача стоила того, чтобы ее решали великие математики.
Ведь в ней шла речь о функциях, у которых аргументами служили кривые линии.
Самое замечательное решение оказалось у Якоба Бернулли.
Он сформулировал принцип: если какая-нибудь кривая обладает свойством максимума или минимума, то каждая ее бесконечно малая часть обладает тем же свойством.
Слайд 14Из истории…
Много задач на нахождение кривых линий, обладающих свойствами экстремума,
И в геометрии новое исчисление оказалось очень полезным. После того, как вывели формулу для длины пространственной кривой, возникла задача: найти кратчайшее расстояние среди всех кривых, соединяющих две точки А и В поверхности и лежащих на этой поверхности.
Например:
на плоскости – отрезок
на сфере – дуга диаметрального сечения
на эллипсоиде вращения – геодезическая линия.
Слайд 16Из истории…
Общий метод решения задач на экстремальные
Метод Лагранжа назвали вариационным исчислением.
Своеобразные вариационные задачи возникают при изучении процессов управления. Это управление самолетами, ракетами, экономическими системами и т. д.
Возникает задача: как осуществить переход из одного состояния в другое, либо в кратчайший срок, либо с наименьшим расходом топлива Экстремальные задачи теории управления изучали советский математик академик Л. С. Понтрягин и его ученики В. Г. Болтянский, Г. В. Гамкрелидзе и Е. Ф.Мищенко. Он разработал особый метод решения получивший название «принцип максимума Понтрягина».
Слайд 17
Разбейте пустыню
Далее разобьем пополам эту половину, затем ту часть, где окажется лев, и т. д. до тех пор, пока размер полученной части станет сравнимым с размерами льва.
Тогда лев окажется в клетке.
Анекдот Как ловить льва в пустыне?
Слайд 18Эксперимент
Из формулы: Ѕ = а в sina площадь параллелограмма будет принимать наибольшее значение при α = 90°( это прямоугольник). Составим таблицу возможных значений для сторон прямоугольника и треугольника при постоянном периметре и вычислим площадь. Например: периметр фигуры равен 12 см.
Прямоугольник Треугольник
Вывод: эксперимент показал, что среди прямоугольников наибольшую площадь имеет квадрат, а среди треугольников – равносторонний треугольник.
Пусть длина окружности равна периметру данной фигуры. Вычислим площадь круга.
С = 2 π ґ, Ѕ = π ґ², т. о. Ѕ = С²/4π = 36 /π ≈ 11,5
Слайд 19Эксперимент
Решим задачу Дидоны при помощи мыльной пленки. Проволочное колечко окунем в мыльный раствор и на пленку положим нитку, связав ее концы. У нитки неправильная форма. Проколем пленку внутри нитки и мыльная пленка, стремясь занять меньшую площадь, мгновенно расправит петлю в правильную окружность!
Итак, экспериментально мы пришли к гипотезе: наибольшую площадь при заданном периметре имеет круг, но всякая гипотеза требует доказательства.
Слайд 20Сказка
В плоскости проходило много линий – и прямые, и кривые, и ломаные. И у всех были свои точки зрения на мир.
- все в мире делится на возвышенное и униженное, - резала правду одна прямая
- нет, отрубила другая, - все в мире – или правые или неправые.
- не ссорьтесь, девочки, - плавно изогнувшись, вмешалась кривая, - все в мире диалектично: здесь ты правый, а тут унижен. Ломаные свое мнение высказывать стеснялись, а окружность формулировала так: - весь мир – или внутренний или остальной. Ну, об остальном мне говорить неинтересно, зато мой внутренний мир богат. Только такие, всесторонние как я…
- плоские личности так много болтают, прервала ее спираль, а что касается мира – то он лишь прослойка между витками, чтоб они не перепутались…
И никто не спрашивал мнения маленькой, незаметной– точки единственной общей точки плоскости и линии, проходившей вне этой плоскости.
Решая задачи, не упускайте на первый взгляд незаметные факты.
Слайд 21Задача Дидоны
Найти прямоугольник наибольшей площади, ограниченный с одной стороны морем,
Решение.
Пусть АВ = х, тогда ВС = ℓ-2х, а Ѕ(х) = х(ℓ-2х) (1) на отрезке [0,ℓ/2]. Преобразуем функцию (1) к виду:
Ѕ(х) = хℓ -2х² = -2(х - ℓ/4)² + ℓ²/8, откуда видно, что функция (1) принимает наибольшее значение при х = ℓ/4
Итак, прямоугольник является половиной квадрата, примыкающей длинной стороной к морю, его площадь
Ѕ = ℓ²/32.
Слайд 22Торопящийся луч света
Законы отражения и преломления света применяются при расчете сложных
Слайд 23Этот принцип дает ключ к разгадке головоломки
Ворона видит двор
Напротив дерева – забор.
Слетай на землю, клюй зерно,
Оно рассыпано давно.
Задача вроде бы проста,
Да остры когти у кота.
Куда слететь,
Схватить зерно и на забор взлететь?
Чтоб от кота вороне упорхнуть,
Тут надобно найти короткий путь.
Замечание: задачу можно решить и геометрически, и алгебраически.
Слайд 24Задача о трех железных дорогах
В лесу,
Живет медведь. Знаток ответь:
Где, В кругу валежней, Меж корнями,
Ему Берлогу надо рыть,
Чтоб до ближайшей Из дорог,
Как можно больше Было расстоянье?
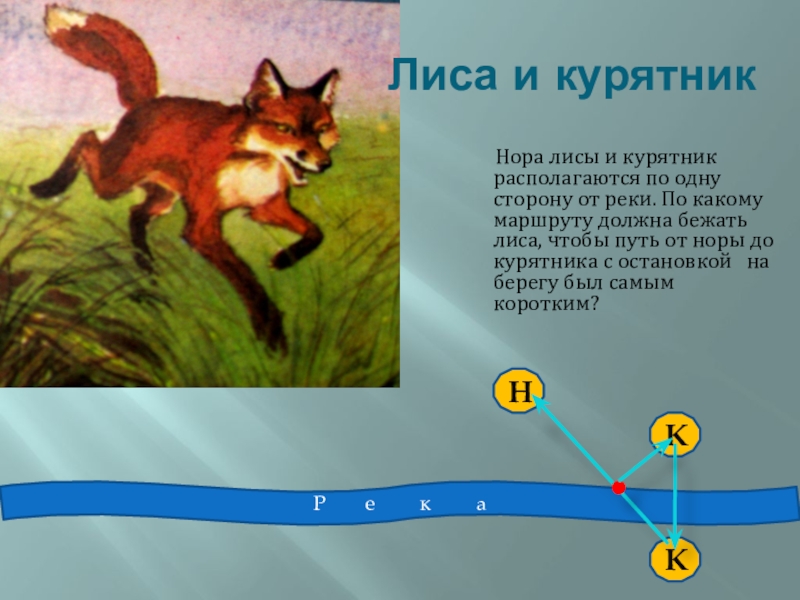
Слайд 25Лиса и курятник
Нора лисы и курятник располагаются
Р е к а
Н
К
К
Слайд 26Задача о крокодилах
В круглом озере живут три крокодила. Где они
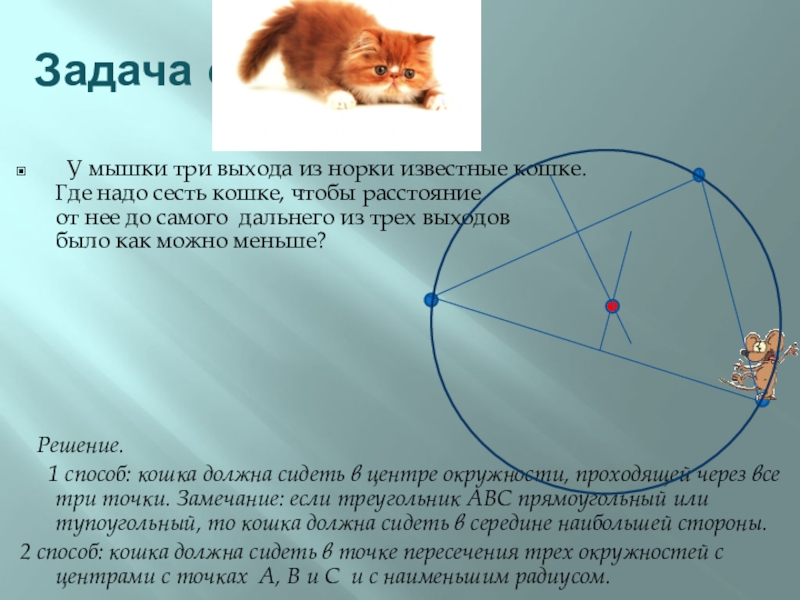
Слайд 28Задача о кошке
У мышки три выхода из норки известные кошке.
Решение.
1 способ: кошка должна сидеть в центре окружности, проходящей через все три точки. Замечание: если треугольник АВС прямоугольный или тупоугольный, то кошка должна сидеть в середине наибольшей стороны.
2 способ: кошка должна сидеть в точке пересечения трех окружностей с центрами с точках А, В и С и с наименьшим радиусом.
Слайд 29Как провести шоссе?
Из приречного города А надо направлять грузы
Слайд 30Канал и плот
Канал имеет прямоугольный поворот. Какой максимальной
Обоснуйте чертеж
Решение:
Слайд 31Бумажный змей
Змею, имеющему вид кругового сектора, желают придать такую форму, чтобы
Решение. Пусть ґ – радиус сектора, ℓ - дуга, р –периметр, Ѕ – площадь, тогда р = 2ґ+ ℓ, Ѕ(ґ) = ґ ℓ/2 = ґ (р - 2ґ)/2 = ґ р - 2ґ²/2 (1). Функция (1) принимает наибольшее значение при ґ = -в/2а (вершина параболы; ветви вниз), т. о. ґ = р/4, тогда ℓ = р/2. Итак, сектор при данном периметре замыкает наибольшую площадь, если его радиус составляет половину дуги.
Слайд 32
Расходы в час
Расходы на топливо будут тем больше, чем быстрее движется судно, остальные же расходы от скорости не зависят. Чем медленнее движется корабль, тем дешевле его эксплуатация? Нет! Поскольку расходы нужно рассчитывать не на 1 час, а на 1 км пути.
Возникает задача: какой должна быть скорость парохода, чтобы общая сумма расходов на 1 км пути была наименьшей, если расходы на топливо за 1час пропорциональны квадрату скорости?
Решение: пусть Ѕ – сумма расходов в час, а V – скорость судна, тогда расходы на 1км пути найдем по формуле: Ѕ/Ѵ. По условию Ѕ = ķѴ²+в, где ķ – коэффициент пропорциональности, в – другие расходы (кроме топлива).
Итак, надо найти значение Ѵ, при котором функция у = ķѴ+в/Ѵ имеет наименьшее значение.
Эту функцию можно исследовать на минимум с помощью производной, поэтому оставим вопрос пока открытым и вернемся к нему в 11-м классе.
Оптимальная скорость
Слайд 34Занимательные задачи Волшебный замок
В замке 3 двери открыты,
Слайд 35Занимательные задачи Найди число
Найди наименьшее натуральное число, которое после
n - ?
2n =n²
3n=n³
Слайд 36Занимательные задачи Три
Бак полон воды. Ее перелили поровну в три бочки. В первой бочке вода заняла 1/2 его объема, во второй – 2/3 , а в третьей – 3/4 объема. Известно, что бак и все три бочки вмещают по целому числу литров.
При каком наименьшем объеме бака это возможно?
Слайд 37Заключение
Нам удалось найти фигуру, имеющую наибольшую площадь при заданном периметре –
Также мы считаем, что работа стоит затраченных усилий, так как мы пополнили свой багаж знаний, получили навыки самостоятельной и совместной работы, а также навыки в поисковой и творческой деятельности.
Мы надеемся, что исторические факты, подбор различных задач и разные методы их решения вызовут интерес и у учеников, и у учителей и будут полезны им при организации элективного курса.
И в завершение мы хотим привести слова
Блеза Паскаля:
Слайд 38
что полезно не упускать случая делать его немного занимательным».
Паскаль