- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад проекта по математике на тему Неевклидовая геометрия (10 класс)
Содержание
- 1. Презентация проекта по математике на тему Неевклидовая геометрия (10 класс)
- 2. Цели исследования:Изучить историю становления геометрии.Выявить, существуют ли
- 3. Геометрия ЕвклидаПервым систематическим изложением геометрии, дошедшим до
- 4. Из каждой точки ко всякой другой точке
- 5. О чем говорится в V постулате Евклида?Если
- 6. Вообразим, что мы взяли две точки А
- 7. В современных аксиоматических изложениях геометрии в качестве
- 8. Долгое время евклидовая геометрия считалась единственно верной,
- 9. Лобачевский в течение 40 лет преподавал в Казанском
- 10. Сохранились студенческие записи лекций Лобачевского (от 1817),
- 11. Лобачевский считает аксиому параллельности Евклида произвольным ограничением.
- 12. Две несовпадающие прямые либо пересекаются
- 13. Плоскости Лобачевского
- 14. Геометрия Лобачевского Лобачевский построил новую геометрию,
- 15. Модель ЛобачевскогоОдной из первых моделей, в которой
- 16. И данная модель не получила противоречия. Отсюда
- 17. Например:вертикальные углы равны; углы при основании равнобедренного
- 18. Однако, теоремы, где применяется аксиома параллельности прямых,
- 19. В геометрии Лобачевского:Два неравных равносторонних треугольника имеют
- 20. Ученые не раз отмечали, что Лобачевский своею
- 21. Геометрия Лобачевского включает в себя геометрию Евклида
- 22. Но помимо Лобачевского были и другие учённые, которые пытались подтвердить или опровергнуть геометрию Евклида. А именно:
- 23. Исследования Саккери Гипотезу тупого угла, допускающую существование
- 24. Исследования Лежандра Французского математик Адриен Мари Лежандр,
- 25. Исследования Гаусса Гаусс обратился к теории параллельных в
- 26. Исследования Януша Больяй Творцом новой геометрии стал так
- 27. Какой геометрией описывается мир, в котором мы живём??
- 28. Сейчас вселенная расширяется, но если масса вещества
- 29. Геометрия Лобачевского в нашем мире Геометрия
- 30. Заключение:Когда Евклид формулировал 5 постулат, вряд ли
- 31. Использованные ресурсы: http://uztest.ru/abstracts/?idabstract=336056 https://ru.wikipedia.org/wiki Энциклопедия по математике
- 32. Спасибо за внимание!
Слайд 1Неевклидовая
Геометрия
Автор проекта: Мартынов Анатолий, ученик 11 «А» класса.
Руководитель:
Учитель математики Гаврилова
Слайд 2Цели исследования:
Изучить историю становления геометрии.
Выявить, существуют ли геометрии, отличные от евклидовой?
Содержание
Узнать о сферах применения геометрии Лобачевского.
Слайд 3Геометрия Евклида
Первым систематическим изложением геометрии, дошедшим до нашего времени, являются “Начала”
Именно «Начала» являются основой евклидовой геометрии, от которой мы и будем отталкиваться. А для этого приведём 5 основных постулатов Евклида:
Слайд 4Из каждой точки ко всякой другой точке можно провести прямую;
Каждую ограниченную
Из любого центра можно описать окружность любого радиуса;
Все прямые углы равны;
И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньше двух прямых, то продолженные эти прямые неограниченно встретятся с той стороны, где углы меньше двух прямых.
Слайд 5О чем говорится в V постулате Евклида?
Если две прямые а и
Слайд 6 Вообразим, что мы взяли две точки А и В на расстоянии
Продолжим прямые а и в, пока они не пересекутся в точке С. В результате получится прямоугольный треугольник АВС, у которого угол А прямой, угол при вершине С равен y и составляет 1 угловую секунду. Катет АС этого треугольника имеет длину с/tg y=2,06*105. Следовательно, длина катета АС составляет приблизительно 2,06*105 м= =206 км (на самом деле немного больше).
Слайд 7В современных аксиоматических изложениях геометрии в качестве неопределяемых терминов обычно рассматриваются
точка – это то, что не имеет частей;
линия – это длина без ширины;
прямая – это линия, которая равно расположена по отношению к точкам на ней;
поверхность – это то, что имеет только длину и ширину;
плоская поверхность есть та, которая равно расположена по отношению к прямым на ней;
граница есть то, что является оконечностью чего-либо.
Определения
Слайд 8Долгое время евклидовая геометрия считалась единственно верной, но потом многие учённые
Никола́й Ива́нович Лобаче́вский (20 ноября (1 декабря) 1792, Нижний Новгород
— 12 (24) февраля 1856, Казань) — русский математик, создатель
неевклидовой геометрии, деятель университетского образования и народного просвещения. Известный английский математик Уильям Клиффорд назвал Лобачевского «Коперником геометрии»
Слайд 9Лобачевский в течение 40 лет преподавал в Казанском университете, в том числе
Немного биографии
Николай — средний из троих сыновей Прасковьи Александровны Лобачевской, мужем которой был чиновник в геодезическом департаменте Иван Максимович Лобачевский (1760—1800).
В 1802 году Прасковья Александровна отдала всех троих сыновей в Казанскую гимназию, единственную в те годы во всей восточной части Российской империи, на «казённое разночинское содержание». Николай Лобачевский окончил гимназию в конце 1806 года, показав хорошие знания, особенно по математике и языкам —латинскому, немецкому, французскому. Вскоре после поступления Николая в гимназию, расширяются возможности для получения дальнейшего образования. 5 ноября 1804 года император Александр I подписывает «Утвердительную грамоту» и «Устав Императорского Казанского университета», куда и поступает Николай.
Слайд 10Сохранились студенческие записи лекций Лобачевского (от 1817), где им делалась попытка
Это сочинение стало первой в мировой литературе серьёзной публикацией по неевклидовой геометрии, или геометрии Лобачевского.
Слайд 11Лобачевский считает аксиому параллельности Евклида произвольным ограничением. С его точки зрения,
(1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского
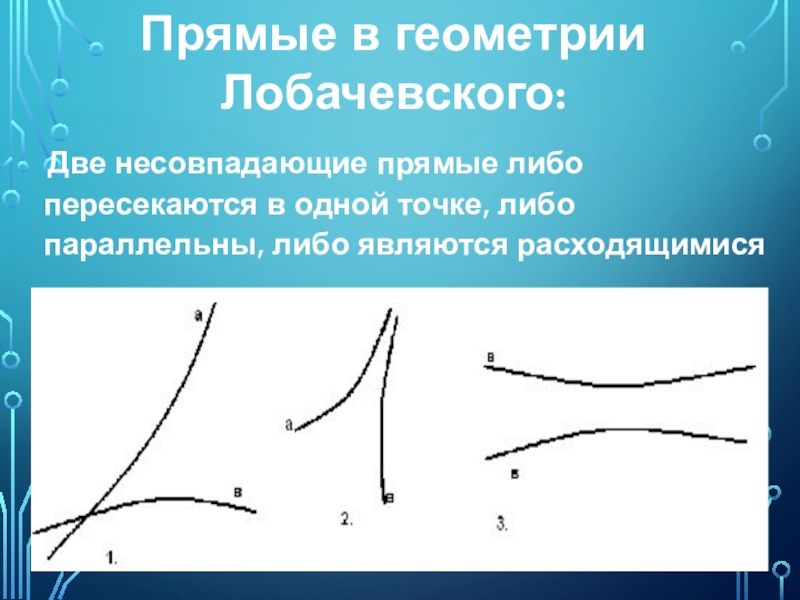
Слайд 12 Две несовпадающие прямые либо пересекаются в одной точке, либо
Прямые в геометрии Лобачевского:
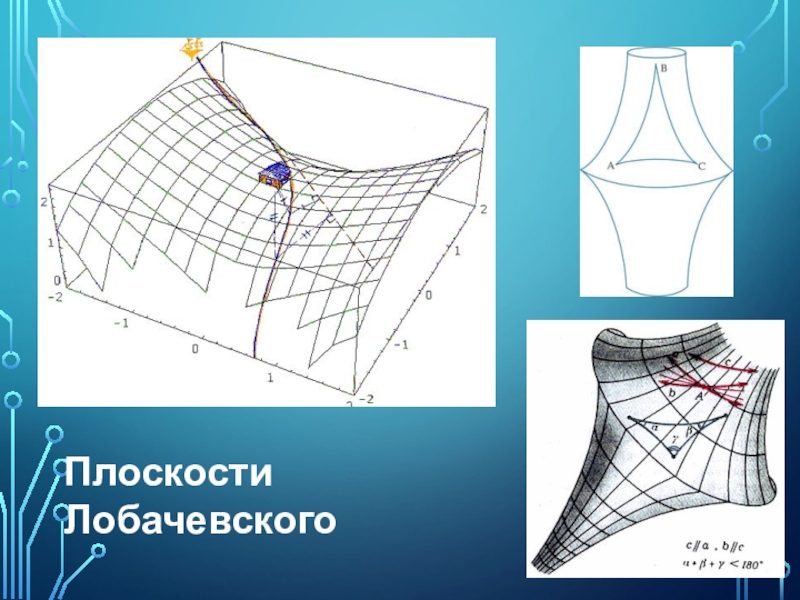
Слайд 14Геометрия Лобачевского
Лобачевский построил новую геометрию, откинув постулат Евклида, заменив
Слайд 15Модель Лобачевского
Одной из первых моделей, в которой «работает» геометрия Лобачевского, является
Пусть даны неевклидова прямая AB и точка C вне ее. Бесконечное множество прямых, проходящих через точку C , не пересекают хорду-прямую AB. А следовательно аксиома Лобачевского верна для этой модели.
Слайд 16И данная модель не получила противоречия.
Отсюда следует, что таких прямых
Доказывая много десятков теорем, не обнаруживая логических противоречий, Лобачевскому пришла в голову догадка о непротиворечивости такой геометрии, он назвал её воображаемой.
В геометрии Лобачевского сохраняются все теоремы, которые в евклидовой геометрии можно доказать без использования пятого постулата.
Слайд 17Например:
вертикальные углы равны;
углы при основании равнобедренного треугольника равны;
из данной
и др.
Слайд 18Однако, теоремы, где применяется аксиома параллельности прямых, видоизменяются:
Теорема о
Формула для площади треугольника S=k*D, то есть площадь связана с его дефектом. Самую большую площадь имеет треугольник с нулевыми углами, а его стороны имеют бесконечную длину.
Слайд 19В геометрии Лобачевского:
Два неравных равносторонних треугольника имеют неравные углы.
В геометрии
Если углы одного треугольника равны соответственно углам другого треугольника, то эти треугольники равны.
Геометрическое место точек, находящихся на данном расстоянии от данной прямой и лежащих по одну сторону есть кривая линия, которая называется эквидистантой.
Слайд 20Ученые не раз отмечали, что Лобачевский своею геометрией совершил прорыв в
Слайд 21Геометрия Лобачевского включает в себя геометрию Евклида не как частный, а
Пространство Лобачевского есть пространство трех измерений, отличающееся от нашего тем, что в нем не имеет места постулат Евклида. Основываясь на работах Лобачевского и постулатах Римана, Альберт Эйнштейн создал теорию относительности, подтвердившую искривленность нашего пространства. Теория Эйнштейна была многократно подтверждена астрономическими наблюдениями, в результате которых стало ясно, что геометрия Лобачевского является одним из фундаментальных представлений об окружающей нас Вселенной.
Слайд 22Но помимо Лобачевского были и другие учённые, которые пытались подтвердить или
Слайд 23Исследования Саккери
Гипотезу тупого угла, допускающую существование четырехугольника, у которого четвертый
Итальянец Саккери рассматривал четырехугольник с тремя прямыми углами (рис. 3). Четвертый угол (обозначим его через ф) мог оказаться прямым, тупым или острым. Саккери установил, что гипотеза прямого угла, т.е. утверждение о том, что четвертый угол ф всегда равен 900, позволяет доказать пятый постулат. Иначе говоря, гипотеза прямого угла представляет собой новую аксиому, эквивалентную пятому постулату.
Слайд 24Исследования Лежандра
Французского математик Адриен Мари Лежандр, в каждом издании книги,
Но неизменно в следующем издании автор, признавая, что в его рассуждении использовалось некое утверждение (не сформулированное им явно) - "очевидное", но в действительности представлявшее собой новую аксиому, эквивалентную пятому постулату.
Ни одна из попыток Лежандра не привела к успеху.
Слайд 25Исследования Гаусса
Гаусс обратился к теории параллельных в 1792 г. Сначала он надеялся
В 1817 г. в одном из писем признался: "Я прихожу все более к убеждению, что необходимость нашей геометрии не может быть доказана". Но обнародовать эти идеи он не решился из боязни быть непонятым.
Гаусс не опубликовал ни один из своих результатов, хотя из его писем и личных бумаг видно, что он разработал основные положения неевклидовой геометрии.
Слайд 26Исследования Януша Больяй
Творцом новой геометрии стал так же и венгерский математик
Результаты Яноша Больяя были сжато изложены в 1832 г. в приложении книге его отца, Фаркаша Больяя. Труд Я. Больяя "Приложение, содержащее науку о пространстве, абсолютно истинную, не зависящую от истинности или ложности XI аксиомы Евклида (что a priori никогда решено быть не может)" обычно кратко называют "Аппендикс" (от лат. "приложение").
Слайд 28Сейчас вселенная расширяется, но если масса вещества всей вселенной превысит определенный
Слайд 29Геометрия Лобачевского в нашем мире
Геометрия Лобачевского находит свое применение
в географии
в теории чисел
в теории относительности
в астрономии
в релятивистской физике
в физике высоких энергий
в теории функции комплексного переменного
Слайд 30Заключение:
Когда Евклид формулировал 5 постулат, вряд ли он знал, какую бурю
Лобачевский, отказавшись от 5 постулата, не знал, что его «воображаемая геометрия» на поверку окажется реальной.
Доказательства к геометрии Евклида существуют, но они не всегда работают, как например физика Ньютона.
Для жизненного пользования вполне подходит и евклидовая геометрия, поэтому от неё никто не отказывается, и её преподают в школах.
Неевклидовые геометрии существуют, и они не противоречат геометрии Евклида полностью, а только лишь её части.
Нельзя сказать, что неевклидовая геометрия единственно правильная. Может быть через несколько лет она устареет и окажется неверной.
Неевклидовая геометрия изучается так как, она может описать всё пространство целиком, в отличии от евклидовой.
Слайд 31Использованные ресурсы:
http://uztest.ru/abstracts/?idabstract=336056
https://ru.wikipedia.org/wiki
Энциклопедия по математике «Аванта».
Александров Г.С. «Несколько
Джавард Тарджеманов «Юность Лобачевского» (http://www.livelib.ru/book/1000903665)
и т.д.