- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад проекта по математике на тему Способы решения систем уравнений (7-9)класс
Содержание
- 1. Презентация проекта по математике на тему Способы решения систем уравнений (7-9)класс
- 2. Содержание.
- 3. ОпределениеУравнение – это равенство, содержащее одну или
- 4. Основные понятия. Система уравнений.Определения:Системой уравнений называетсянекоторое количество
- 5. Способы решения систем уравненийСпособ подстановкиМетод деления и
- 6. Способ подстановкиАлгоритм решения.Выражают одну переменную через другую
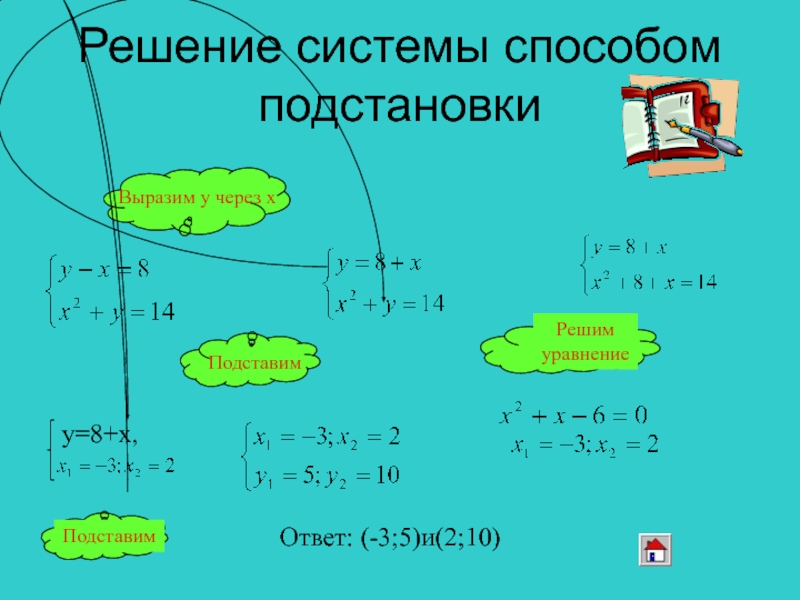
- 7. Решение системы способом подстановкиОтвет: (-3;5)и(2;10)
- 8. Способ сложения Алгоритм решения. Уравнять
- 9. Решение системы способом сложения||·(-1)+____________Ответ: (-3;5)и(2;10)
- 10. Графический способАлгоритм решения. Построить в одной системе
- 11. Решение системы графическим способом202x4610-2yy=8+хВыразим учерез хПостроим графикпервого уравненияу=8+хПостроим графиквторого уравненияОтвет: (-3;5)и(2;10)Парабола, ветви вниз(0;14)-вершина 12148
- 12. Способ сравненияВыразить у через х (или
- 13. 7х – 1 = 2х - 4Решим
- 14. Привести систему уравнений к простейшей часто удается
- 15. Пример: Решите систему уравнений:
- 16. Метод деления и умножения.Решение систем методом умножения
- 17. Разделим первое уравнение на второеОтвет: (5; 3)Выразим у через хРешение системы методом деления
- 18. Метод определителей. Алгоритм решения.Составить табличку (матрицу) коэффициентов
- 19. -80 Составим матрицу
- 20. 7х + 2у = 1
- 21. Линейные системы трех уравнений с тремя неизвестными.Решением
- 22. Гаусс Карл Фридрих (30.04.1777 - 23.02.1855)Немецкий математик, внёсший фундаментальный вклад также
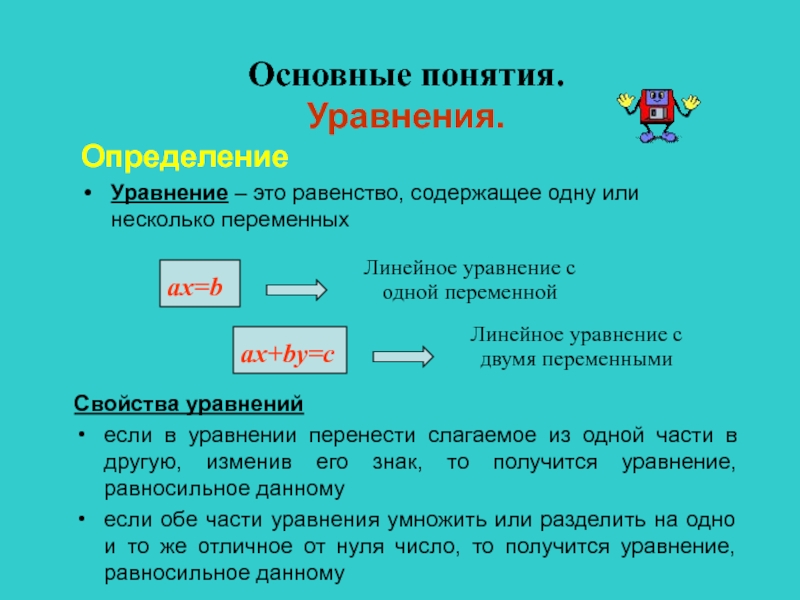
Слайд 3Определение
Уравнение – это равенство, содержащее одну или несколько переменных
Линейное уравнение с
одной
Линейное уравнение с
двумя переменными
Свойства уравнений
если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному
если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному
Основные понятия.
Уравнения.
Слайд 4Основные понятия.
Система уравнений.
Определения:
Системой уравнений называется
некоторое количество уравнений,
объединенных фигурной скобкой.
Фигурная скобка
уравнения должны выполняться одновременно.
Решением системы уравнений
называется значения переменных, обращающие
каждое уравнение системы в верное равенство.
Решить систему уравнений
это значит - найти все её решения или установить, что их нет.
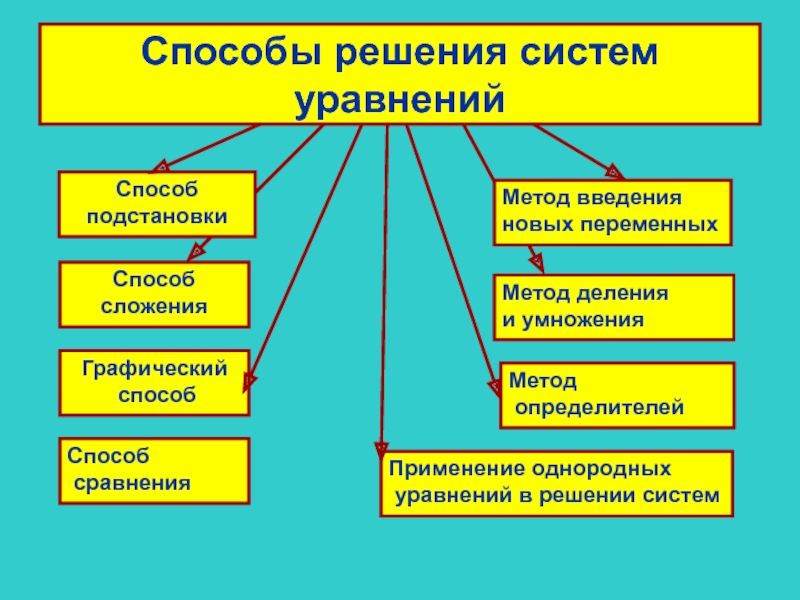
Слайд 5Способы решения систем уравнений
Способ
подстановки
Метод деления
и умножения
Способ
сложения
Метод введения
новых
Метод
определителей
Применение однородных
уравнений в решении систем
Способ
сравнения
Графический
способ
Слайд 6Способ подстановки
Алгоритм решения.
Выражают одну переменную через другую
в одном
2. Это выражение подставляют в другое уравнение системы,
и в результате получают уравнение с одной переменной.
3. В уравнении с одной переменной находят корень.
4. Подставив найденный корень, получают значение другой переменной.
5. Записывают ответ.
Слайд 8Способ сложения
Алгоритм решения.
Уравнять модули коэффициентов при какой-нибудь переменной
Сложить почленно уравнения
Составить новую систему: одно уравнение новое, другое - одно из старых
Решить новое уравнение и найти значение одной переменной
Подставить значение найденной переменной в старое уравнение и найти значение другой переменной
Записать ответ: х=…; у=… .
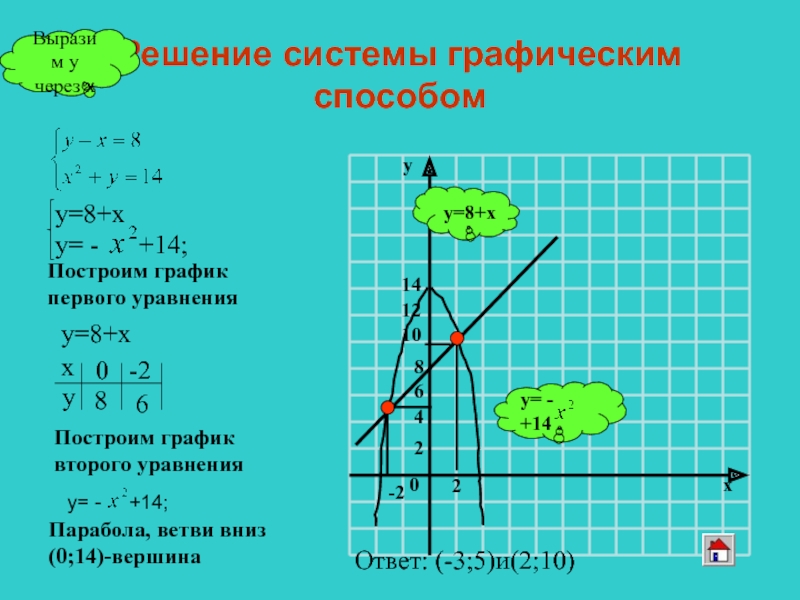
Слайд 10Графический способ
Алгоритм решения.
Построить в одной системе координат график каждого уравнения
Определить координаты
Записать ответ: х=…; у=… , или (х; у)
Слайд 11Решение системы графическим способом
2
0
2
x
4
6
10
-2
y
y=8+х
Выразим у
через х
Построим график
первого уравнения
у=8+х
Построим график
второго уравнения
Ответ: (-3;5)и(2;10)
Парабола,
(0;14)-вершина
12
14
8
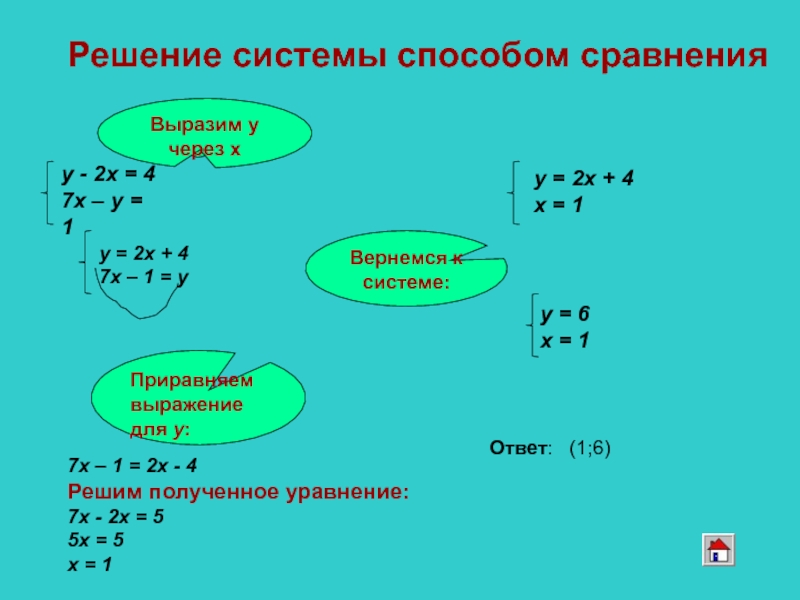
Слайд 12Способ сравнения
Выразить у через х (или х через у) в
2. Приравнять выражения, полученные для одноимённых переменных.
3. Решить полученное уравнение и найти значение одной переменной.
4. Подставить значение найденной переменной в одно из выражений
для другой переменной и найти её значение.
5. Записать ответ: х =…; у =… .
Алгоритм решения.
Слайд 13
7х – 1 = 2х - 4
Решим полученное уравнение:
7х - 2х
5х = 5
х = 1
Решение системы способом сравнения
Вернемся к системе:
Ответ: (1;6)
Приравняем выражение для у:
Слайд 14Привести систему уравнений к простейшей часто
удается с помощью замены переменных.
или
Метод введения новых переменных.
Слайд 15
Пример: Решите систему уравнений:
х + ху + у =2
Решение:
(х + у)2 –ху=4
(х + у) + ху=2
Сделаем замену х + у= u; ху= v, получим:
u2 –v =4 u2+u – 6 =0 u1 = 2; u2 = -3
u + v = 2 v = 2- u v1 = 0; v2 = 5
Осталось решить две простейшие системы:
х + у =3 х1 = 0; х2=2
ху = 0 у1 = 2; у2 =0
х + у =3
ху =5 - решений нет
Ответ: ( 0;2 ) ( 2;0 )
1.
2.
Слайд 16Метод деления и умножения.
Решение систем методом умножения и деления основано на
следующих правилах:
Если обе части уравнения f2( х;у ) = g2( х;у )
ни при каких значениях ( х;у ) одновременно в ноль не обращаются,
то системы равносильны.
Слайд 17Разделим первое уравнение на второе
Ответ: (5; 3)
Выразим у через х
Решение системы
Слайд 18Метод определителей.
Алгоритм решения.
Составить табличку (матрицу) коэффициентов при неизвестных
2. Найти - определитель Δx, получаемый из Δ заменой первого столбца
на столбец свободных членов.
3. Найти - определитель Δy, получаемый из Δ заменой второго столбца
на столбец свободных членов.
4. Найти значение переменной х по формуле (Крамера)
5. Найти значение переменной у по формуле
6. Записать ответ: х =…; у =… .
Слайд 19-80
Составим матрицу из коэффициентов
при неизвестных Δ
=
= 1·6 - 2·(-9) = 6 + 18 = 24
= 7·(-9) - 1·17 = - 63 -17= -80
Составим определи-
тель Δx, заменив в определи-
теле Δ первый столбец
на столбец свободных
членов
Составим определи-
тель Δy, заменив в определи-
теле Δ второй столбец
на столбец свободных
членов
Δx
х=
Δ
=
24
8
=
3;
у=
Δy
Δ
=
8
= -10.
Найдем
х и у
Ответ: х=3; у= -10.
Решение системы методом определителей.
Слайд 20
7х + 2у = 1
17х + 6у =
Составим матрицу из коэффициентов при неизвестных
Составим определитель Δx , заменив в определителе Δ
первый столбец на столбец свободных членов.
Δx = 1 2
-9 6 = 1*6 - 2*(-9) = 6 + 18 = 24
Составим определитель Δy , заменив в определителе Δ
второй столбец на столбец свободных членов.
Δy = 7 1
17 -9 = 7*(-9) - 1*17 = -63 – 17 = -80
=
=
Ответ: х = 3; у =10.
7 2
17 6
= 7*6 - 2*17 = 42 – 34 = 8
=
Найдем х и у:
Х=
=
=
-10
3
У=
Слайд 21Линейные системы трех уравнений
с тремя неизвестными.
Решением линейной системы трех уравнений
тройка чисел (x,y,z)
удовлетворяющая каждому уравнению системы.
Любая линейная система может быть решена
методом последовательного исключения неизвестных
( метод Гаусса).
Слайд 22Гаусс Карл Фридрих (30.04.1777 - 23.02.1855)
Немецкий математик, внёсший фундаментальный
вклад также в астрономию и геодезию,
иностранный чл.-корр. (с 31.01.1802) и
иностранный почётный чл.(с 24.03.1824)
Петербургской АН. Родился в семье водопроводчика.
Учился в Гёттингенском университете (1795—98).
В 1799 получил доцентуру в Брауншвейге,
в 1807 — кафедру математики и астрономии в
Гёттингенском университете, с которой была также
связана должность директора Гёттингенской
астрономической обсерватории. На этом посту Гаусс
оставался до конца жизни.
Отличительными чертами творчества Гаусса являются глубокая органаничная связь в его исследованиях между теоретической и прикладной математикой,
необычайная широта проблематики. Работы Гаусса оказали большое влияние на развитие алгебры, теории чисел, дифференциальной геометрии, теории тяготения, классической теории электричества и магнетизма, геодезии,
целых отраслей теоретической астрономии.