- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Проект дифференцированный подход в обучении математике обучающихся
Содержание
- 1. Презентация Проект дифференцированный подход в обучении математике обучающихся
- 2. Формула обучения «овладение = усвоение + применение знаний на практике»
- 3. Цель дифференциации процесса обучения –обеспечить каждому
- 4. Чешский педагог 17 века Ян Амос Коменский:
- 5. Процентное соотношение учащихся по уровню обучаемости65 процентов
- 6. Основные правила технологии разноуровневого обученияОсновные правила технологии
- 7. В настоящее время перед
- 8. Качества, которыми должен обладать выпускник:- гибко адаптироваться
- 9. По данным исследований, в памяти
- 10. «Я услышал и забыл, я увидел и
- 11. Тренажер для устного счетаВычислить 1В.
- 12. Тренажер для устного счета. Вычислить.
- 13. Тематические тесты . Графики функций А5. График
- 14. Решение неравенств методом интервалов.А7. Решите неравенство А7. Решите неравенство
- 15. Нахождение множества значений функции. А8. Укажите множество значений
- 16. Тематические тесты . В1. Укажите наименьшее натуральное решение неравенства Решение неравенств методом интервалов..
- 17. Тематические тесты. Решить тригонометрическое уравнениеС1. Решите уравнение
- 18. Самостоятельная работа«Иррациональные уравнения»
- 19. Самостоятельная работа. «Логарифмические уравнения и неравенства»
- 20. Самостоятельная работа. «Объём пирамиды» Вариант 1Основание пирамиды
- 21. Задачи с профессиональной направленностьюПрофессия «Парикмахер»Как приготовить из
- 22. Задачи с профессиональной направленностьюПрофессия «Электромонтер станционного оборудования
- 23. Задачи с профессиональной направленностьюПрофессия « Повар»Напиток «Летний»
- 24. Карточки-задания. Логарифмические неравенства
- 25. Олимпиада по математике 1. В один сосуд
- 26. РАЗРАБОТКА РАЗНОУРОВНЕВОГО УРОКА ПО АЛГЕБРЕ
- 27. Цель урока:Тип урока: закрепление изученного материала.Цели урока:
- 28. «Производная функции» Цели изучения урока распределяются по
- 29. Пояснительная запискаУчебные карты № 1 – 4
- 30. УЧЕБНая карта № 1Цель: закрепление темы «Производная»,
- 31. Таблица производных
- 32. Учебная карта № 1. Самостоятельная работа (
- 33. УЧЕБНая карта №2 Цель: закрепить умения находить
- 34. УЧЕБНая карта №3 Цель: Закрепить навык нахождения
- 35. УЧЕБНая карта №4 Цель: Закрепить навык нахождения
- 36. Учебная карта №5 Цель: Применять полученные знания
- 37.
- 38. Науку все глубже постигнуть стремись,
- 39. ЦЕЛИ И ЗАДАЧИ УРОКА 1.Образовательная:-обобщение, углубление,
- 40. Цели урока: - показать красоту математики, ее роль
- 41. Структура урока. 1.Организационный момент (1 мин.)2.Сообщение темы, целей
- 42. План путешествияДобро пожаловать в страну"МАТЕМАТИКУ"Исторический районСалон красотыМатематическое кафе «Эврика»Край математических знанийМатематическая таможняПоле математических чудес
- 43. Девиз: « УСЕРДИЕ ВСЕ ПРЕВОЗМОГАЕТ» Край применения
- 44. «Логика есть искусство, которое упорядочивает и связывает
- 45. Слайд 45
- 46. А теперь, ребята, в городе Эрудитов посетим
- 47. Слайд 47
- 48. Меню
- 49. Итак, приступим к праздничному обеду. Как всегда,
- 50. Задание 3. А теперь, пока не остыл
- 51. Задание 5. Решите кроссворд «И в шутку и всерьез».
- 52. По горизонтали: 1.Название нашего кафе.По вертикали: 2.
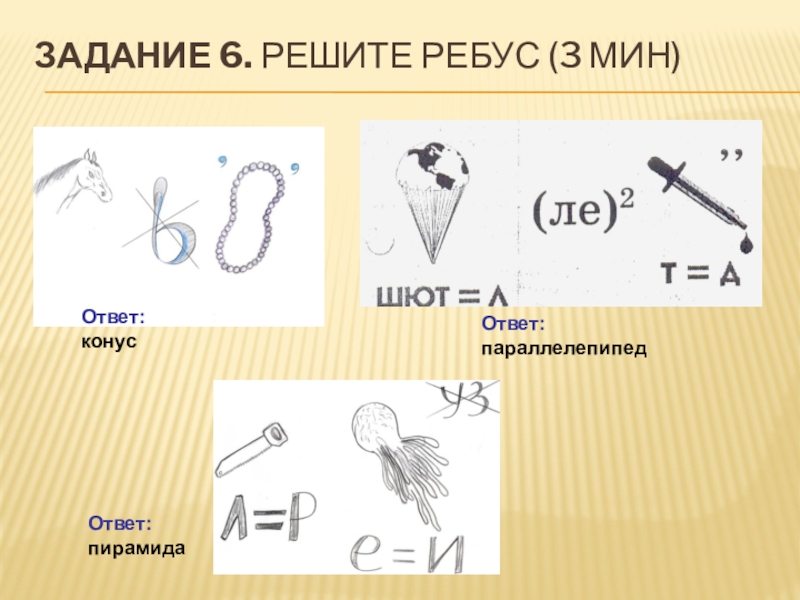
- 53. Задание 6. Решите ребус (3 мин) Ответ: конусОтвет: пирамидаОтвет: параллелепипед
- 54. Задание 7. Всем командам одинаковые задания c
- 55. Задание 8.Решите логические задачи. 1.Три брата –
- 56. Задание 9. Сочините буриме, то есть
- 57. Поле математических чудес. 1. Лист Мёбиуса. Кто
- 58. Стихотворение великого математика 19 в. Софьи Ковалевской
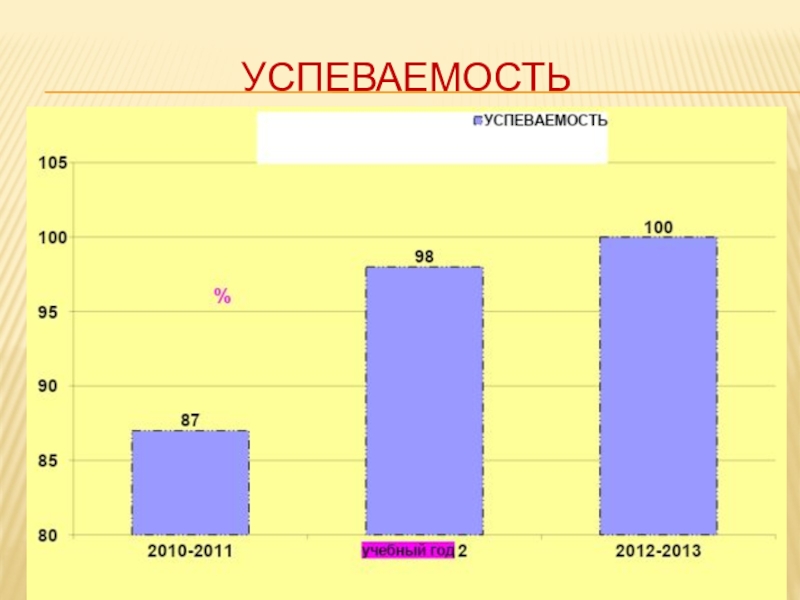
- 59. уСПЕВАЕМОСТЬ
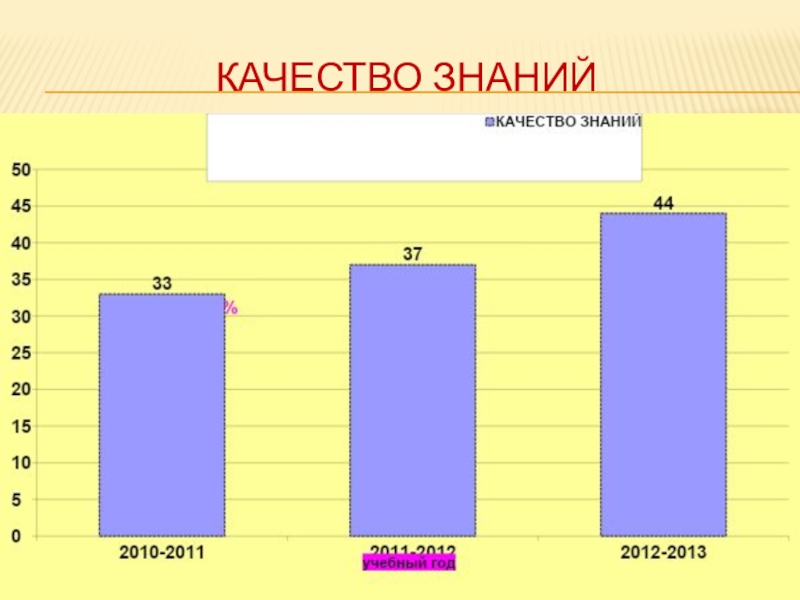
- 60. КАЧЕСТВО ЗНАНИЙ
Слайд 1
Проект
«Дифференцированный подход в обучении математике
обучающихся»
(из опыта работы)
Преподаватель математики
высшей категории
ГБОУ СПО «Лабинский медицинский колледж»
Федорова Мария Дмитриевна
Г. Лабинск
Слайд 3 Цель дифференциации процесса
обучения –обеспечить каждому
учащемуся условия для максимального
развития его способностей, склонностей,
удовлетворения познавательных
интересов, потребностей
в процессе освоения содержания
образования.
Слайд 4Чешский педагог 17 века Ян Амос Коменский:
«Мы решаемся обещать
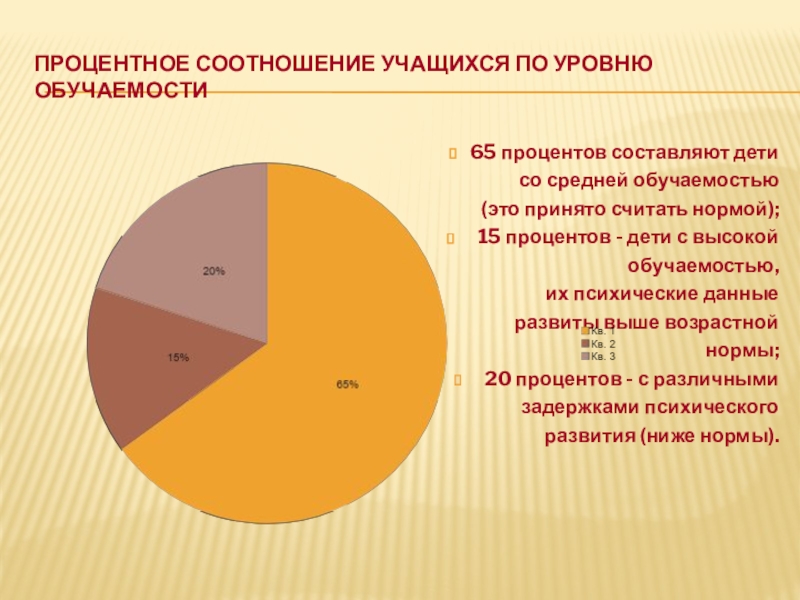
Слайд 5Процентное соотношение учащихся по уровню обучаемости
65 процентов составляют дети
со средней
(это принято считать нормой);
15 процентов - дети с высокой
обучаемостью,
их психические данные
развиты выше возрастной
нормы;
20 процентов - с различными
задержками психического
развития (ниже нормы).
Слайд 6Основные правила технологии разноуровневого обучения
Основные правила технологии разноуровневого обучения можно свести
1. Не дотягивать всех учащихся до единого уровня, а создавать условия каждому в меру его потребностей, сил и желания.
2. Последовательное освоение и сдача уровней.
3. За одно занятие можно сдать только одну тему.
4. Для получения оценки «3» необходимо знание не менее 50 % из числа предложенных в данный период времени тем,
на «4» – 70–80 %, на «5» – 90–100 %.
5. При подготовке к практическому занятию можно выбрать любой уровень заданий и повысить свою обычную отметку.
6. Основными принципами являются: доброжелательность, взаимопомощь, нормотворчество, право на собственное мнение и ошибку.
Слайд 7 В настоящее время перед образованием стоит проблема -
Слайд 8Качества, которыми должен обладать выпускник:
- гибко адаптироваться в меняющихся жизненных ситуациях,
- критически и творчески мыслить, четко осознавать, где и каким образом приобретаемые знания могут быть применены в окружающей действительности;
- самостоятельно работать над развитием собственного интеллекта, нравственности, физического состояния, культурным уровнем;
- грамотно работать с информацией (уметь собирать, анализировать, сопоставлять, обобщать, устанавливать закономерности, формулировать выводы и т.д.), в том числе с помощью компьютера и других средств информационных и коммуникационных технологий;
- быть коммуникабельным, уметь работать в различных группах.
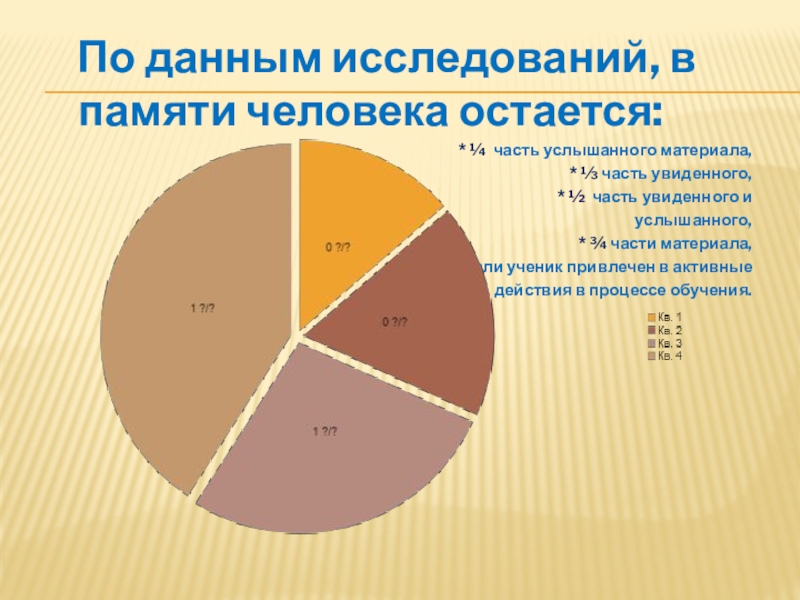
Слайд 9 По данным исследований, в памяти человека остается:
* ¼
* ⅓ часть увиденного,
* ½ часть увиденного и
услышанного,
* ¾ части материала,
если ученик привлечен в активные
действия в процессе обучения.
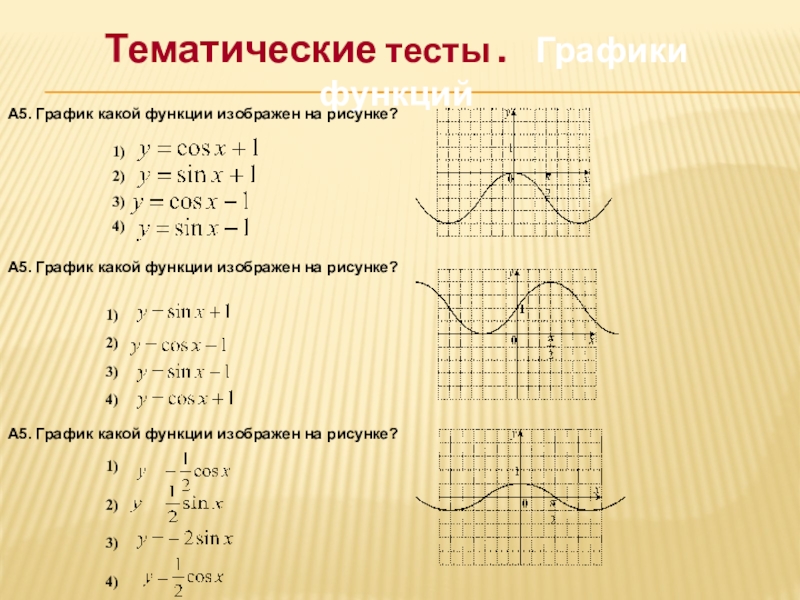
Слайд 13Тематические тесты . Графики функций
А5. График какой функции изображен на
А5. График какой функции изображен на рисунке?
А5. График какой функции изображен на рисунке?
Слайд 14Решение неравенств методом интервалов.
А7. Решите неравенство
А7. Решите неравенство
.
Тематические тесты .
А7. Решите неравенство
.
А7. Решите неравенство
.
Слайд 15Нахождение множества значений функции.
А8. Укажите множество значений функции
А8. Какое число не
А3. Из данных чисел выберите число, принадлежащее множеству значений функции
А6. Укажите область значений функции
.
Тематические тесты .
Слайд 16Тематические тесты .
В1. Укажите наименьшее натуральное решение неравенства
Решение неравенств методом
.
Слайд 20Самостоятельная работа. «Объём пирамиды»
Вариант 1
Основание пирамиды — ромб со стороной 4
Вариант 2
Основанием пирамиды служит треугольник со сторонами 5 см, 12 см и 13 см. Каждое боковое ребро пирамиды наклонено к основанию под углом 45°. Найти объем пирамиды.
Вариант 3
В основании пирамиды — равнобедренная трапеция с боковой стороной 6 см и углом 30°. Боковые грани пирамиды наклонены к основанию под углом 60°. Найти объем пирамиды.
Слайд 21Задачи с профессиональной направленностью
Профессия «Парикмахер»
Как приготовить из 30%-го и 3% раствора
Две краски надо смешать так, чтобы одной из них было на 30% боль- ше, чем другой. Сколько процентов смеси составит каждая краска?
Слайд 22Задачи с профессиональной направленностью
Профессия «Электромонтер станционного оборудования и телефонной связи»
Два телеграфных
Кабель диаметром 42 мм заключается в свинцовую оболочку толщиной 200 мм. На изготовление оболочки израсходована 1 т свинца. Какова длина кабеля? Плотность свинца 11,4 г/см3.
Слайд 23Задачи с профессиональной направленностью
Профессия « Повар»
Напиток «Летний» содержит 50% сои, 14%
Печенье содержит 10% белка, 16% жира, 60% углеводов. Сколько белка, жира и углеводов содержится в 400 г такого печенья?
Ячмень содержит 60% крахмала, а рис-75%. Для приготовления крахмала взяли 400 г ячменя и 300 г риса. Из какого зерна крахмала получится больше?
При помоле пшеницы получается 80% муки, а при помоле ржи – 75%. Для помола взяли 4 ц пшеницы и 5 ц ржи. Какой муки получится меньше?
Слайд 25Олимпиада по математике
1. В один сосуд входит 3 л., а в
2. Я задумал число, прибавил к нему 1, умножил сумму на 2, произведение разделил на 3 и отнял от результата 4. Получилось 5. Какое число я задумал?
3. Дана дробь . Какое число нужно прибавить к обоим членам этой дроби, чтобы она обратилась в ?
4. При каких значениях х произведение (3х-5)(х+4)(2-х)
а) равно 0; б) положительно; в) отрицательно
5. На две партии разбившись, забавлялись обезьяны.
Часть восьмая их в квадрате
В роще весело резвилась,
Криком радостным двенадцать
Воздух свежий оглашали…
Вместе сколько, ты мне скажешь, обезьян там было в роще?
Слайд 26РАЗРАБОТКА РАЗНОУРОВНЕВОГО
УРОКА
ПО АЛГЕБРЕ И НАЧАЛАМ АНАЛИЗА
тема: «Производная функции»
Преподаватель
высшей категории
Федорова М.Д.
г. Лабинск
Слайд 27Цель урока:
Тип урока: закрепление изученного материала.
Цели урока:
Обеспечить повторение, обобщение и
Способствовать формированию умений применять приемы обобщения, развитию математического кругозора, мышления, внимания и памяти, развивать самостоятельность, самоконтроль, аккуратность.
Воспитывать активность.
Слайд 28«Производная функции»
Цели изучения урока распределяются по трем уровням:
Уровень А -
Уровень В - включает все, что достигнуто на I уровне, но в более сложном виде;
Уровень С - включает все, что достигнуто на I и II уровнях, но теперь должно применяться в нестандартных ситуациях.
В результате овладения содержанием темы учащиеся должны уметь:
Уровень А- находить простейшие производные функций по формулам;
Уровень В - находить производные функций, самостоятельно выбирать метод решения;
Уровень С - применять полученные знания в нестандартных ситуациях.
Слайд 29Пояснительная записка
Учебные карты № 1 – 4 соответствуют уровням подготовки А
Каждая учебная карта содержит указания учителя о том, что нужно знать и уметь, или краткие пояснения к выполнению заданий, или ссылки на учебник, где можно найти нужные объяснения, а также список заданий.
Прочитав указания учителя, ученик выполняет самостоятельные работы, которые включены в карту, и проверяет их по эталонам решений. Эталон учитель демонстрирует ученику, когда тот объявляет о завершении самостоятельной работы. Ученик сравнивает свои ответы с эталонными и исправляет ошибки.
Если он выполнил менее половины заданий, то решает задания другого варианта, которые аналогичны тем, в которых он допустил ошибки.
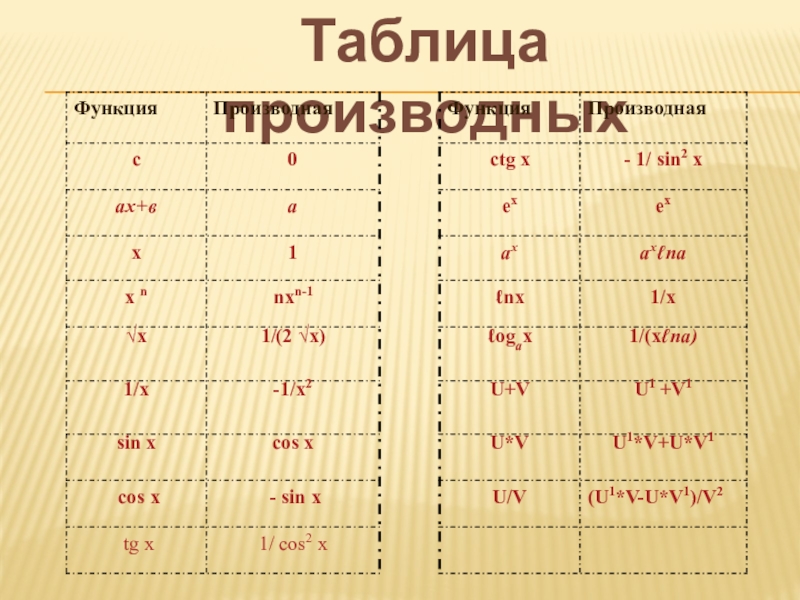
Слайд 30УЧЕБНая карта № 1
Цель: закрепление темы «Производная», отработка навыков нахождение простых
Указания учителя: Вспомните основные правила вычисления производных.
Таблица производных прилагается.
(Прочитайте текст на стр. 113-116 учебника под редакцией А. Н. Колмогорова)
Слайд 32Учебная карта № 1.
Самостоятельная работа ( 15 мин)
Найти производные фунцкий:
f(x)=25 f(x)=19
f(x)=4x f(x)=3x
f(x)=8x2 f(x)=7x3
f(x)=x14 f(x)=x6
f(x)=17x3 f(x)=10x2
f(x)=10x2 f(x)=x-2
f(x)=x2+6x f(x)=x3+8x
f(x)=x5-7x2+8 f(x)=x2+3x-1
f(x)=7ех-2ах f(x)= 3ех-5ах
f(x)=3ℓnх f(x)=5ℓnх
Слайд 33УЧЕБНая карта №2
Цель: закрепить умения находить производные функции по формулам произведения
Указания учителя: Вспомните правила вычисления производных по правилу №2 и №3 учебник А. Н. Колмогорова (стр. 114).
(U * V)'=U'V+UV'
(U/V)'=(U'V - UV')/V2
Самостоятельная работа №2 (на 15 минут)
Найдите производную функции и вычислите ее значения при Х , равном -1 и 1 , если
I вариант II вариант
f(x)=(3x-4)(2x+5) f(x)=(2x-3)(1-x2)
f(x)=x2(8+7x-x3) f(x)=x3(4+2x-x2)
У=(2х-3)/(5-6х) У=(4х+2)/(7-4х)
У=(5-2х)/(1+3х2) У=(2х-3)/(4-5х2)
Слайд 34УЧЕБНая карта №3
Цель: Закрепить навык нахождения производных тригонометрических функций.
Указания учителя: Внимательно
А. Н. Колмогорова стр. 121.
Вспомните производные синуса, косинуса, тангенса и котангенса.
(sin x)'=cosx (cos x)'=- sinx
(tg x)'=1/cos2x (сtg x)'=-1/sin2x
Самостоятельная работа №3 (на 15 минут)
Найдите производную каждой из функций.
I вариант II вариант
y=2sin x y=-0,5sin x
y=1-cos x y=2-3cos x
y= tg x y=4ctg x
y=2sin x+5cos x y=3cos x - 4sin x
y=(3+4cos x)(5-3sin x) y=(1-2sin x)(2-cos x)
y=5ctg x-4х y= 3tg x+5х
Слайд 35УЧЕБНая карта №4
Цель: Закрепить навык нахождения производной сложной функции
Указания учителя: Внимательно
№1, №2, №3.
F'(g(х)) = F'(g) g'(х)
Самостоятельная работа №4 (на 15 минут)
Найдите производную каждой из функций.
1 вариант 2 вариант
f(x)=(2x-7)8 f(x)=(9x+5)4
f(x)=(x3-2x2+3)17 f(x)=(x3+4x2-8)15
f(x)= 1/(3х2-5) f(x)= 1/(3-2х2)
f(x)= е3х-2*54х f(x)= е2х+4 *27х
f(x)= ℓоg3(6х-1) f(x)= ℓоg5(2-5х)
Слайд 36Учебная карта №5
Цель: Применять полученные знания в вычислении производных в нестандартной
Указания учителя: Вы прошли I и II уровень усвоения материала.
Теперь вам самостоятельно придется выбирать правила нахождения производных функций. Необходимо вспомнить весь материал по нахождению простых и сложных функций.
Прочтите текст учебника А. Н. Колмогорова п. 15-17 стр.113-123.
Самостоятельная работа №5 (на 20 минут)
I вариант II вариант
Найдите значения производных следующих функций в точках х=0 и х=2
y=(5-2x4)7 y=(5-7х3)10
y=( 7-8x2)11 +4х y=(х2+3)4 - 5х
у=(1+3х)4/(5х+1) у=(2-5х)3/(4х-3)
Найдите производную функции
у=3Sin2 (2х-3) у=5cos2(3х-1)
у=4ℓog26(х3-5) у=3 ℓog24(2-3х2)
Домашнее задание.
Выполните из учебника под редакцией А. Н. Колмогорова № 208, 209, 231, 232, 224(a, в).
Слайд 37
Урок – путешествие.
Страна «МАТЕМАТИКА»
Предмет: «Математика».
Тема программы: «Обобщающее повторение».
Тема урока: “Обобщающее повторение”.
Преподаватель математики
высшей квалификационной категории
Федорова Мария Дмитриевна
г. Лабинск
Слайд 38
Науку все глубже постигнуть стремись,
Лишь первых познаний блеснет тебе свет,
Узнаешь: предела для знания нет.
Фирдоуси.
Слайд 39
ЦЕЛИ И ЗАДАЧИ УРОКА
1.Образовательная:
-обобщение, углубление, закрепление знаний учащихся;
-использование умений, навыков при
2. Развивающая:
-способствовать развитию и совершенствованию у учащихся логического мышления, памяти, внимания, активности и самостоятельности.
3.Воспитателиная:
-воспитание интереса к математике, как к науке, способствующей
гармоничному развитию личности;
-развитие интереса к учению и потребности, в знаниях;
-умение применять их на практике, в профессии;
-воспитание культуры организации умственного труда у учащихся;
-формирование умения работать самостоятельно и коллективно;
-создания доброжелательной атмосферы.
4.Методическая:
-соблюдение принципов научности и доступность обучения через
актуализацию опорных знаний учащихся;
-обеспечить хорошее качество знаний у большинства учащихся, через методы
активного обучения на этап понимания, применения, оценивания .
Слайд 40
Цели урока:
- показать красоту математики, ее роль в нашей жизни;
- развивать
смекалку и сообразительность учащихся;
- выработать интерес к предмету.
Слайд 41Структура урока.
1.Организационный момент (1 мин.)
2.Сообщение темы, целей урока и формы его
3. Работа по теме урока (39 мин.)
- Вступительное слово преподавателя:
а) о применении математических знаний в нашей жизни (2 мин);
б) об исторических истоках математики как науки (2 мин);
в) о красоте математических формул и выражений (2 мин).
- Решение задач на развитие логики, смекалки, сообразительности (30 мин).
- Математические чудеса (3 мин).
4. Подведение итогов урока (2 мин).
5. Задание на дом (1 мин).
Слайд 42План путешествия
Добро пожаловать в страну
"МАТЕМАТИКУ"
Исторический район
Салон красоты
Математическое кафе «Эврика»
Край математических знаний
Математическая
Поле математических чудес
Слайд 43Девиз: « УСЕРДИЕ ВСЕ ПРЕВОЗМОГАЕТ»
Край применения математических знаний.
Задача 1.
Два
Слайд 44«Логика есть искусство, которое упорядочивает и связывает мысли. Люди ошибаются именно
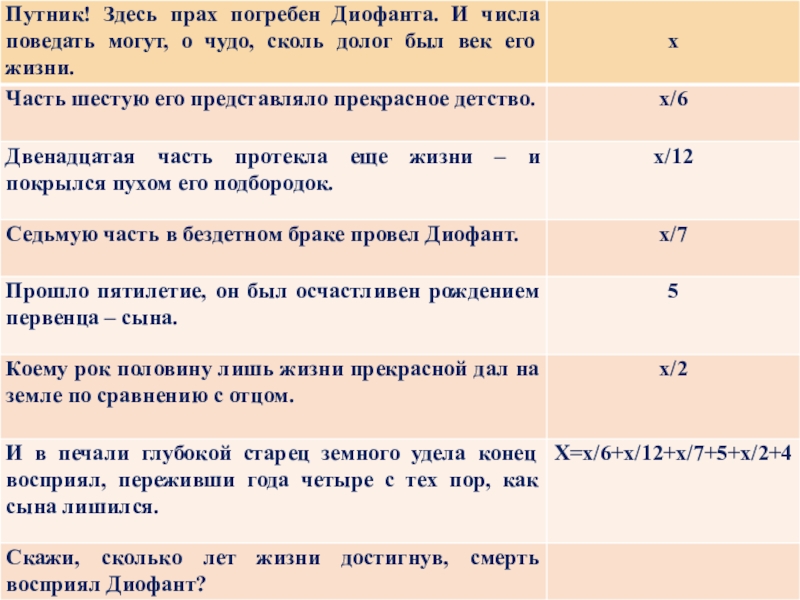
Продолжая мысль о важности математики, я хочу заглянуть назад, то есть обратиться к истории. Если бы не математика, мы бы ничего не узнали о древнем математике ДИОФАНТЕ, жившем в III в. до н.э. История сохранила мало фактов из его биографии. Все, что известно о нем, почерпнуто из надписи на его гробнице – надписи, составленной в форме математической задачи. Вод эта надпись (показ задачи о Диофанте)
Слайд 46А теперь, ребята, в городе Эрудитов посетим Салон красоты, в котором
Древние индусы дали название математике «лилавати», что означает «прекрасная» или «красавица со сверкающими глазами"
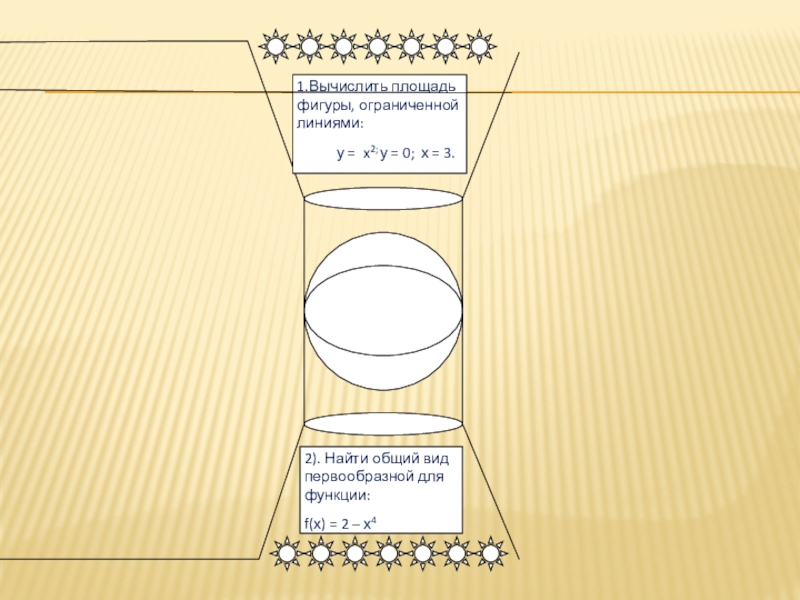
В Салоне красоты я хочу вам предложить модель математического платья. (См. приложения).
Все основные части этой модели состоят из пространственных фигур: цилиндра, шара, усеченного конуса. (Свойства этих фигур вы будете изучать на уроках стереометрии). Красота связи между объемом шара и объемом цилиндра вызвала такое восхищение у Архимеда, что он завещал высечь на своем могильном памятнике чертеж шара, вписанного в цилиндр.
Посмотрите, какие интересные ответы получаются при преобразовании сложных, на первый взгляд, выражений. Они украшают эту модель, как кружева украшают любое платье.
Слайд 49Итак, приступим к праздничному обеду. Как всегда, сначала легкая закуска –
Задание 1. Решите анаграмму. Переставьте буквы так, чтобы получился математический термин.
РИГФАК, АВИНУРЕНЕ, КОЧТА, ВАРТАДК. (График, уравнение, точка, квадрат)
Задание 2. Отгадайте по 3 загадки с числительными.
Какое животное имеет 2 носа? (Носорог: один – на теле, второй – в названии)
Два брата купаются, а третий насмехается. (Два ведра и коромысло)
Двенадцать братьев друг за другом бродят, друг друга не обходят. (Двенадцать месяцев)
Есть семь братьев братьев: годами равные , именами разные. (Дни недели)
Лежит брус на всю Русь. На том брусу 12 гнезд. И во всяком гнезде по четыре птицы. (Год)
Только одно дерево без ветра шумит. Какое? (Осина)
Шесть ног, а бежит не быстрее, чем на четырех. (Всадник на коне)
Два раза родится, а один раз умирает. (Птица)
Сто один брат и все в один ряд. Вместе связаны стоят. Что это? (Изгородь)
Стучит, гремит, вертится. Ничего не боится, считает наш век, а не человек. (Часы)
Четыре ноги, а не зверь. Есть перья, да не птица. (Кровать, постель)
Что имеет два конца, но не имеет начала? (Ножницы)
Слайд 50Задание 3. А теперь, пока не остыл борщ, займемся математическими обгонялками
Назовите автора учебника по алгебре.
Что больше: произведение или сумма всех чисел от -5 до5? (Они равны 0)
Какой знак надо поставить между двумя тройками, чтобы получить число больше двух, но меньше трех? (Запятую)
Назовите автора учебника по геометрии.
Разделите пол сотни на половину. (100)
Что тяжелее: 1 кг ваты или 1 кг железа? (они равны)
Задание 4. Математические смекалки.
Спутники, имеющие одну орбиту, делают оборот вокруг Земли один за 1 ч 40 мин, а другой за 100 мин. Как это объяснить?
(Один и тот же период времени)
В харчевню пришли 11 человек и потребовали подать им по рыбине. К сожалению, у хозяина оказалось всего три небольших рыбины. Тем не менее, хозяин не пожелал упустить случая поживиться: имея в своем распоряжении три рыбы, он обещал гостям подать на стол одиннадцать. Гости заинтересовались этим и даже согласились уплатить деньги вперед. Как хозяин харчевни исполнил свое обещание?
(Уложил рыбу на тарелке так: ХI)
На улице в 11 час вечера идет дождь. Можно ли утверждать, что через 72 ч будет солнечная погода?
(Нет, так как будет ночь)
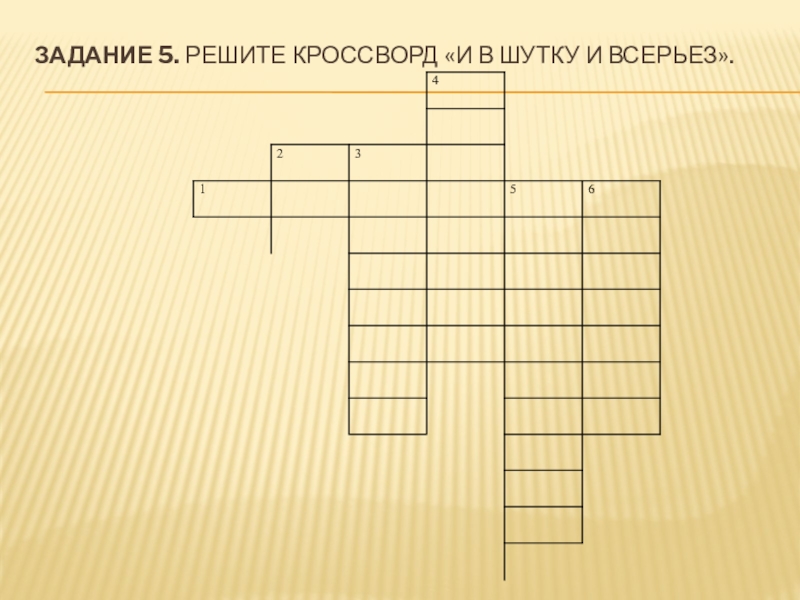
Слайд 52По горизонтали: 1.Название нашего кафе.
По вертикали: 2. Самая нелюбимая оценка ученика.
Ответы:
По горизонтали: 1. Эврика.
По вертикали: 2. Два. 3. Аргумент. 4 Отличник. 5. Контрольная. 6. Аксиома.
Слайд 54Задание 7. Всем командам одинаковые задания c натуральными числами (3 мин).
1. Найдите разность: -- - 8 = ?
(440)
2.К однозначному натуральному числу припишите такую же цифру. Во сколько раз увеличится число?
(11)
3. Тремя двойками, не употребляя знаков действий, напишите возможно большее число.
( 222)
8
8
Слайд 55Задание 8.Решите логические задачи.
1.Три брата – Ваня, Саша, Коля – учились
(Коля, Ваня, Саша.)
2.Трое девушек – Валя, Галя, Катя – пришли на праздничный обед в платьях разного
цвета: одна в сером, другая в белом, а третья в черном. Катя была не в черном платье, Валя не в черном и не в сером. Угадайте, в каком платье была каждая из девушек.
3. В одном классе учатся Иван, Петр, Сергей. Их фамилии – Петров, Сергеев, Иванов. Установите фамилию каждого из ребят, если известно, что Иван по фамилии не Иванов, Петр – не Петров, Сергей – не Сергеев и что Сергей живет в одном доме с Петровым.
(Иван Петров, Петр Сергеев, Сергей Иванов)
Слайд 56Задание 9. Сочините буриме, то есть стихотворение на заданные рифмы.
Рифмы:
пять - опять, восемь - просим.
Гости также могут выполнить это задание.
Слайд 57Поле математических чудес.
1. Лист Мёбиуса. Кто слышал об этом чуде? (Выслушать
Рассказ преподавателя. Лист Мёбиуса был открыт в 1858 году Лейпцигским профессором Августом Мёбиусом, учеником знаменитого Гаусса. Получить его очень просто: склеиваем из бумажной полоски кольцо, только перед склеиванием повернем один конец полоски на 180 . Что же неожиданного увидел Мёбиус у этого кольца? А то, что у листа Мёбиуса одна сторона. Сейчас я вам это докажу (можно пригласить кого – то из ребят). Фломастером, не отрывая его от листа, можно провести линию с обеих сторон полосы, начиная с любого места.
Что произойдет, если я сейчас разрежу по этой линии лист Мёбиуса? Он превратится в одно кольцо, перекрученное, которое будет уже двусторонним.
Свойство односторонности Мёбиуса используется в технике: если в ременной передаче ремень сделать в виде листа Мёбиуса, то его поверхность будет изнашиваться вдвое медленнее, чем у обычного кольца. Это дает ощутимую экономию.
Слайд 58Стихотворение великого математика 19 в. Софьи Ковалевской (1850-1891). И пусть это
Если ты в жизни хотя на мгновенье
Истину в сердце своем ощутил,
Если луч света сквозь мрак и сомненье
Ярким сияньем твой путь озарил:
Чтобы в решеньи своем неизменном
Рок не назначил тебе впереди,
Память об этом мгновенье священном
Вечно храни, как святыню в груди.
Тучи сберутся громадой нестройной,
Небо покроется черною мглой,
С ясной решимостью, с верой спокойной,
Бурю ты встреть и померься с грозой.
В этом стихотворении выражено стремление к познаниям, умение преодолевать все преграды, которые встречаются на пути.