- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Применение интерактивных форм и методов обучения
Содержание
- 1. Презентация Применение интерактивных форм и методов обучения
- 2. ОБЪЕКТ МАТЕМАТИКИ – ВЕСЬ МИР
- 3. «Страшная это опасность –
- 4. ПОЗНАВАТЕЛЬНАЯ АКТИВНОСТЬ ВКЛЮЧАЕТ:Мотивы и цели деятельности.Интерес к
- 5. Слайд 5
- 6. "Если поручить двум
- 7. ЦЕЛИ ОБУЧЕНИЯ МАТЕМАТИКИОвладение теоретическими сведениями, необходимыми для
- 8. МЕТОД ПРОБЛЕМНОГО ОБУЧЕНИЯ. Основой
- 9. КОМПЛЕКСНЫЕ ЧИСЛА.Решить уравнение:
- 10. . С помощью комплексных чисел исследуется течение
- 11. ЗАДАНИЕ ДЛЯ ИССЛЕДОВАНИЯКакой геометрической формы должен быть
- 12. ЭВРИКА!Вывод: шаровой чайник остывает медленнее, чем чайник того же объема любой другой формы
- 13. ЗАДАЧА: Имеется кастрюля объёмом
- 14. Не будем спорить –будем вычислять.Г. Лейбниц
- 15. ТРЕБОВАНИЯ К ПРАКТИЧЕСКИМ ЗАДАЧАМ.Задачи должны иметь реальное
- 16. Сколько обоев необходимо для оклеивания комнаты размером
- 17. ПРИМЕНЕНИЕ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ.По закону показательной функции размножалось
- 18. Математика настолько серьёзный
- 19. Функции в пословицах.
- 20. У русского народа
- 21. «СВЕТИТ, ДА НЕ ГРЕЕТ.»xyХ-количество света. У- количество тепла.
- 22. «КАК АУКНЕТСЯ, ТАК И ОТКЛИКНЕТСЯ».У-ответ на поступкиХ-поступки(добрые, злые)XY
- 23. «ЧЕМ ДАЛЬШЕ В ЛЕС, ТЕМ БОЛЬШЕ ДРОВ.» XY
- 24. «ДОЛГО ДУМАЛ, ДА НИЧЕГО НЕ ВЫДУМАЛ.»Идеи, придумки, задумки, yВремя (час), x
- 25. « ПОМЕНЬШЕ ГОВОРИ, ПОБОЛЬШЕ УСЛЫШИШЬ.»У Количество услышанногоХ Количество разговора
- 26. « КТО ЛЮБИТ ТРУДИТЬСЯ, ТОМУ ЕСТЬ ЧЕМ ГОРДИТЬСЯ.»гордостьтруд
- 27. «УМ ХОРОШО, А ДВА ЛУЧШЕ».У-количество идей, замыслов.Х-количество умов12
- 28. « СИЛА ЕСТЬ, УМА НЕ НАДО». у-силаХ-ум
- 29. Слайд 29
- 30. Слайд 30
- 31. Скажи мне, и я забуду,Покажи мне, и
- 32. Слайд 32
- 33. МЕТОД АЛГОРИТМИЧЕСКОГО ОБУЧЕНИЯ. Задача
- 34. ФУНКЦИИ АЛГОРИТМАПри объяснении нового материала алгоритм играет
- 35. ГАЛЕРЕЯ ЗНАМЕНИТЫХ МАТЕМАТИКОВ
- 36. Михаил ВасильевичЛомоносовВеликий русский ученый
- 37. АНДРЕЙ НИКОЛАЕВИЧ КОЛМОГОРОВ
- 38. СОФЬЯ КОВАЛЕВСКАЯИстория жизни
- 39. ПИФАГОР САМОССКИЙПИФАГОР Самосский (6 в. до н.
- 40. «…так же как и в искусстве, в
- 41. Математика владеет не только истиной, но и
- 42. водаземлявоздухогоньВселеннаядодекаэдргексаэдроктаэдрикосаэдртетраэдрПифагор
- 43. : «Мой дом построен по законам самой
- 44. СНЕЖИНКИ – ЗВЁЗДЧАТЫЕ МНОГОГРАННИКИА вы видели тени
- 45. МНОГОГРАННИКИ В ЮВЕЛИРНОМ ДЕЛЕ
- 46. МНОГОГРАННИКИ В АРХИТЕКТУРЕ
- 47. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ПЛОСКОСТИ
- 48. ОСНОВНЫЕ ЦЕЛИ ОЛИМПИАДЫ.Расширение кругозора обучающихся.Развитие интереса к
- 49. Задача 1.В сказочной стране поблизости один от
- 50. Задача 2.Кощей Бессмертный зарыл клад на глубину
- 51. ИСПРАВЛЯЕМ ОШИБКИПри проверке домашнего задания.Делаю ошибки сознательно,
- 52. Например: «Докажем», что 2>3: Найдите ошибку.
- 53. Перпендикулярность прямых и плоскостей
- 54. Многогранники Урок - лекцияГеометрия
- 55. The End…
- 56. Слайд 56
- 57. ФОРМИРОВАНИЕ УСТОЙЧИВЫХ ИНТЕРЕСОВ Разнообразие, творческий характер
- 58. Учиться можно только весело.
ОБЪЕКТ МАТЕМАТИКИ – ВЕСЬ МИР
Слайд 3
«Страшная это опасность – безделье за партой; безделье
шесть часов ежедневно, безделье месяцы и годы. Это развращает».
В. А. Сухомлинский
В. А. Сухомлинский
Слайд 4ПОЗНАВАТЕЛЬНАЯ АКТИВНОСТЬ ВКЛЮЧАЕТ:
Мотивы и цели деятельности.
Интерес к предмету.
Внимание к изучаемому объекту.
Волевые
усилия.
Положительные усилия.
Творческую самостоятельность.
Владение необходимыми способами и приёмами познавательной деятельности.
Положительные усилия.
Творческую самостоятельность.
Владение необходимыми способами и приёмами познавательной деятельности.
Слайд 6
"Если поручить двум людям, один из которых
математик, выполнение любой незнакомой работы, то результат всегда будет следующим: математик сделает её лучше"
Д.Юнг
Д.Юнг
Слайд 7ЦЕЛИ ОБУЧЕНИЯ МАТЕМАТИКИ
Овладение теоретическими сведениями, необходимыми для изучения других дисциплин и
специальностей.
Воспитание математической культуры.
Развитие алгоритмического и логического мышления.
Умение строить математическую модель.
Умение использовать справочный материал.
Воспитание математической культуры.
Развитие алгоритмического и логического мышления.
Умение строить математическую модель.
Умение использовать справочный материал.
Слайд 8МЕТОД ПРОБЛЕМНОГО ОБУЧЕНИЯ.
Основой метода проблемного обучения является
создание проблемной ситуации, формулировка проблемы, подведение обучающихся к проблеме.
Задача проблемной ситуации – направить деятельность обучающихся на максимальное овладение изучаемым материалом, обеспечить мотивационную сторону деятельности, вызвать интерес к ней.
Задача проблемной ситуации – направить деятельность обучающихся на максимальное овладение изучаемым материалом, обеспечить мотивационную сторону деятельности, вызвать интерес к ней.
Слайд 10
. С помощью комплексных чисел исследуется течение воды и полет самолетов
и ракет. Применяются они при вычерчивании географических карт. Используются комплексные числа для изучения явлений в атомах и атомных ядрах и т.д. Использование методов теории функции комплексной переменной используется при построении фракталов, которые в последние время стали очень популярны.
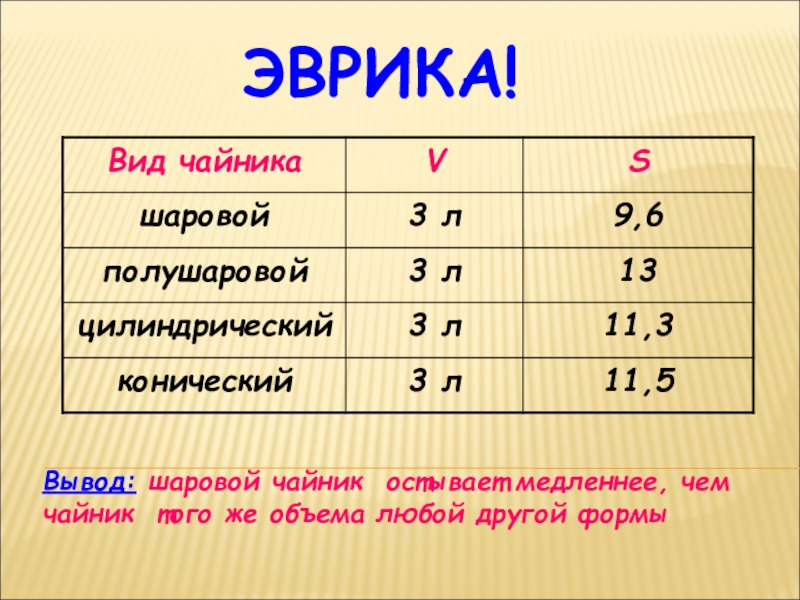
Слайд 11ЗАДАНИЕ ДЛЯ ИССЛЕДОВАНИЯ
Какой геометрической формы должен быть чайник. Чтобы вода в
нём остывала как можно дольше. (изменяя форму чайника, объём и материал, из которого он изготовлен не менять)
Слайд 12ЭВРИКА!
Вывод: шаровой чайник остывает медленнее, чем чайник того же объема любой
другой формы
Слайд 13
ЗАДАЧА:
Имеется кастрюля объёмом 3 литра. Необходимо увеличить
один размер кастрюли на 5 см (высоту или радиус), чтобы объём увеличился максимально.
Слайд 15ТРЕБОВАНИЯ К ПРАКТИЧЕСКИМ ЗАДАЧАМ.
Задачи должны иметь реальное практическое содержание, которое показывает
практическую значимость математических знаний.
Задачи должны показывать взаимосвязь смежных дисциплин на конкретных примерах.
Задачи должны соответствовать учебным программам.
Численные данные в задачах должны быть реальными.
Задачи должны показывать взаимосвязь смежных дисциплин на конкретных примерах.
Задачи должны соответствовать учебным программам.
Численные данные в задачах должны быть реальными.
Слайд 16
Сколько обоев необходимо для оклеивания комнаты размером 3м×3,5м×2,7м. (длина рулона -
10м, ширина - 1м 6см).
Слайд 17ПРИМЕНЕНИЕ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ.
По закону показательной функции размножалось бы все живое на
Земле, если бы для этого имелись благоприятные условия, т. е. не было естественных врагов и было вдоволь пищи.
Если бы все маковые зерна давали всходы, то через
5 лет число "потомков" одного растения равнялось
приблизительно 2000 растений на 1 м2 суши.
Потомство комнатных мух за лето только от
одной самки может составить 8 · 1014 шт.
Эти мухи весили бы несколько миллионов тонн.
В природе, технике и экономике встречаются многочисленные процессы, в ходе которых значение величины меняется в одно и то же число раз, т. е. по закону показательной функции.
Если бы все маковые зерна давали всходы, то через
5 лет число "потомков" одного растения равнялось
приблизительно 2000 растений на 1 м2 суши.
Потомство комнатных мух за лето только от
одной самки может составить 8 · 1014 шт.
Эти мухи весили бы несколько миллионов тонн.
В природе, технике и экономике встречаются многочисленные процессы, в ходе которых значение величины меняется в одно и то же число раз, т. е. по закону показательной функции.
Слайд 18
Математика настолько серьёзный предмет, что нельзя упускать
возможности сделать его немного занимательным.
Б. Паскаль.
Б. Паскаль.
Слайд 20
У русского народа существует бесчисленное множество пословиц,
поговорок, загадок. Они создавались народом в течении многовековой истории и отражают его жизнь, условия труда, культуру. Они отражают взаимосвязи между различными жизненными категориями, т. е. фактически являются отражениями функциональных зависимостей и доказывают, что функция – сама жизнь !
Слайд 31
Скажи мне, и я забуду,
Покажи мне, и я, может быть, запомню,
Вовлеки
меня, и я пойму.
Конфуций.(450 г. до н. э.)
Конфуций.(450 г. до н. э.)
Слайд 33МЕТОД АЛГОРИТМИЧЕСКОГО ОБУЧЕНИЯ.
Задача алгоритмического метода – выработать
определённые навыки решения той или иной проблемы.
В ходе решения задачи обучающийся рассуждает в соответствии с некоторыми алгоритмическими предписаниями, которые ему даны или сформулированы им самостоятельно.
В ходе решения задачи обучающийся рассуждает в соответствии с некоторыми алгоритмическими предписаниями, которые ему даны или сформулированы им самостоятельно.
Слайд 34ФУНКЦИИ АЛГОРИТМА
При объяснении нового материала алгоритм играет роль образца – набора
последовательности действий.
При ответе студента у доски, алгоритм служит образцом ответа.
Алгоритм позволяет предупреждать типичные ошибки.
При составлении алгоритма развивается логическое мышление.
Развивается устная и письменная речь.
Алгоритм даёт возможность выполнять осознанные действия.
Алгоритм учит выделять главное.
При работе с алгоритмом развивается математическая грамотность.
При ответе студента у доски, алгоритм служит образцом ответа.
Алгоритм позволяет предупреждать типичные ошибки.
При составлении алгоритма развивается логическое мышление.
Развивается устная и письменная речь.
Алгоритм даёт возможность выполнять осознанные действия.
Алгоритм учит выделять главное.
При работе с алгоритмом развивается математическая грамотность.
Слайд 39ПИФАГОР САМОССКИЙ
ПИФАГОР Самосский (6 в. до н. э.), древнегреческий философ, религиозный
и политический деятель, основатель пифагореизма, математик. Пифагору приписывается изучение свойств целых чисел и пропорций, доказательство теоремы Пифагора и др.
Слайд 40
«…так же как и в искусстве, в науке важную роль играет
понятие красоты… Красиво, когда разнородные и прежде не связанные явления вдруг объединяются в стройные формулы. Красота науки и в логической стройности и в богатстве связей»
Б. Мигдал.
Б. Мигдал.
Слайд 41Математика владеет не только истиной, но и высшей красотой - красотой
отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.
Бертран Рассел
Бертран Рассел
Слайд 43: «Мой дом построен по законам самой строгой архитектуры.
Сам Евклид
мог бы поучиться, познавая геометрию моих сот».
Слайд 44СНЕЖИНКИ – ЗВЁЗДЧАТЫЕ МНОГОГРАННИКИ
А вы видели тени от снежинок?
А вы знаете,
как они танцуют
В лунном блеске голубом и чистом
Или просто в свете фонаря?
В лунном блеске голубом и чистом
Или просто в свете фонаря?
Слайд 48ОСНОВНЫЕ ЦЕЛИ ОЛИМПИАДЫ.
Расширение кругозора обучающихся.
Развитие интереса к изучению математики.
Развитие творческих способностей
обучающихся.
Развитие способности обучающихся применять полученные знания в нестандартных ситуациях.
Повышение качества подготовки специалиста.
Развитие способности обучающихся применять полученные знания в нестандартных ситуациях.
Повышение качества подготовки специалиста.
Слайд 49
Задача 1.
В сказочной стране поблизости один от другого находятся города А
и В. Все жители города А говорят только правду, а жители города В всегда лгут. Жители этих городов ходят друг к другу в гости. Путешественник попал в один из этих городов, но не знает в какой. Как он может задав один вопрос первому попавшемуся жителю, узнать, в каком городе он находится?
Слайд 50
Задача 2.
Кощей Бессмертный зарыл клад на глубину 1 м. Этого ему
показалось недостаточно, он откопал клад, углубил колодец до 2 м и снова зарыл. Этого ему снова показалось мало, он отрыл клад, углубил яму 3 м и зарыл. Затем он проделал тоже, углубив колодец до 4м,5 м, и т.д. Известно, что колодец глубиной n метров Кощей выкапывает за n2 дней. Известно также, что на 1001-й день Кощей умер от непосильной работы. На какой глубине остался клад?
Слайд 51ИСПРАВЛЯЕМ ОШИБКИ
При проверке домашнего задания.
Делаю ошибки сознательно, при решении задач на
доске.
Делаю ошибки в чертежах к задачам.
Делаю ошибки в чертежах к задачам.
Слайд 57ФОРМИРОВАНИЕ УСТОЙЧИВЫХ ИНТЕРЕСОВ
Разнообразие,
творческий характер
деятельности,
перспективность деятельности,
возможность приложения к практике,
познание нового,
атмосфера дружелюбия и увлечённости.
перспективность деятельности,
возможность приложения к практике,
познание нового,
атмосфера дружелюбия и увлечённости.
Слайд 58
Учиться можно только весело.
Чтоб переваривать знания, надо
поглощать их с аппетитом.
Анатоль Франс
Анатоль Франс