Автор:
Овчарова Ирина
МОУ «ООШ» с. Шепелевка
6 класс
Руководитель:
Сидорова Татьяна Евгеньевна ,
учитель математики первой категории
МОУ «ООШ» с. Шепелевка
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Приемы быстрого счета
Содержание
- 1. Презентация Приемы быстрого счета
- 2. «Мозг, так же как и мускулы, развивается, когда его тренируют.»
- 3. Изучение почти любого предмета в школе предполагает
- 4. Цель нашего исследования - диагностика уровня развития
- 5. СПОСОБЫ БЫСТРОГО СЛОЖЕНИЯ ЧИСЕЛПоразрядное сложение двузначных чиселК
- 6. Сложение путем последовательного прибавления к одному числу
- 7. Сложение путем округленияЕсли слагаемые близки к круглым
- 8. Сложение с использованием свойств действий с числамиСлагаемые
- 9. Сложение десятичных дробей путем поразрядного сложения, начиная
- 10. СПООБЫ БЫСТРОГО ВЫЧИТАНИЯ ЧИСЕЛ Поразрядное вычитание574 -
- 11. Вычитание с использованием свойств действий с числами1358
- 12. .Вычитание путем уравнивания числа единиц последних разрядов
- 13. Вычитание путем округления уменьшаемого или вычитаемого или
- 14. . СПОСОБЫ БЫСТРОГО УМНОЖЕНИЯ ЧИСЕЛ3.1 Умножение на
- 15. 3.2 Умножение на 5; 50; 0,5; 25;
- 16. Чтобы умножить число на 2,5, нужно умножить
- 17. Чтобы умножить число на 0,25, нужно разделить
- 18. 53 * 5 = 26 * 10
- 19. 3.3 Умножение на 1,5 и на 15.Чтобы
- 20. 3.4 Умножение на 111 способ.Чтобы число умножить
- 21. 3.5 Умножение двузначного числа на 101 и
- 22. 3.7 Применение распределительного закона умножения относительно сложения
- 23. 4. СПОСОБЫ БЫСТРОГО ДЕЛЕНИЯ ЧИСЕЛ4.1 Последовательное делениеЕсли
- 24. 4.3 Деление на 25; 2,5; 0,25 Чтобы
- 25. 5. Возведение в квадрат числа, оканчивающегося цифрой
- 26. Практическая часть работы включала изучение динамики развития
- 27. Для диагностики были составлены 4 блока однотипных
- 28. Обработка результатов показала:На начальном этапе было выполнено
- 29. На этом этапе выполнено из 27 заданий
- 30. Слайд 30
- 31. ЗАКЛЮЧЕНИЕНеобходимым условием успешной работы, так или иначе
- 32. Слайд 32
- 33. Слайд 33
- 34. ЛитератураГольштейн Д.Н. Техника быстрых вычислений. - М.,
Слайд 1 НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ УЧАЩИХСЯ
Динамика развития вычислительных навыков с помощью приемов быстрого
Слайд 3Изучение почти любого предмета в школе предполагает хорошие знания математики, и
В обыденной повседневной жизни мы тоже не можем обойтись без математики, а именно без ее вычислительной составляющей. Так как часто встречаемся с разного рода расчетами, измерениями, просто даже не замечая этого.
В наш век новых технологий и развития компьютерной техники разговор об устном счете может показаться неуместным, однако и по сей день гибкость ума является предметом гордости людей, а способность, например, быстро производить в уме вычисления вызывает откровенное удивление.
Слайд 4Цель нашего исследования - диагностика уровня развития вычислительных навыков с использованием
Задачи исследования:
изучение способов быстрого устного счета;
подбор материалов для тренинга;
проведение диагностики;
изучение результатов исследования;
разработка схем быстрого умножения и деления на 0,5; 5; 50;25; 2,5; 0,25; 125; 12,5; 1,25; 0,125; 9; 99; 999.
Слайд 5СПОСОБЫ БЫСТРОГО СЛОЖЕНИЯ ЧИСЕЛ
Поразрядное сложение двузначных чисел
К разрядам первого слагаемого прибавляют
76 + 38 + 47 + 86 + 45 = (70 + 30 + 40 + 80 + 40) +(6 + 8 + 7 + 6 + 5) = 260 + 32= 292.
Слайд 6Сложение путем последовательного прибавления к одному числу отдельных разрядов другого числа,
К разрядам первого слагаемого прибавляют разряды другого слагаемого.
56 + 47 = (56 + 40) + 7 = 96 + 7 = 103;
8375 + 473 = ((8375 + 400) + 70) + 3 = (8775 + 70) + 3 = 8845 + 3 = 8848.
Слайд 7Сложение путем округления
Если слагаемые близки к круглым числам, то их заменяют
3916+991+1998+2002=(4000+1000+2000+2000)–(84+9+2)+2=9000–95+2=8907
Слайд 8Сложение с использованием свойств действий с числами
Слагаемые разбивают на такие группы,
12 + 63 + 28 = (12 + 28) + 63 = 40 + 63 = 103;
3013 + 74 + 2187 + 126 = (3013 + 2187) + (74 + 126) =5200 + 200 = 5400.
Прибавляют к какому-нибудь числу сумму чисел; можно прибавлять к данному числу каждое слагаемое отдельно
863 + (346 + 137) = 863 + 346 + 137 = 863 +137+ 346 = 1000 + 346 = 1346.
Если одно слагаемое близко к круглому числу, то его заменяют разностью и дополнением между круглым числом
549 + 94 = 549 + (100 – 6) = 549 + 100 – 6 = 643.
Если оба слагаемых близки к круглому числу, то они заменяются разностью между круглым числом и дополнением
298 + 397 = 300 – 2 + 400 – 3 = 700 – 5 = 695;
504 + 497 = 500 + 4 + 500 – 3 = 1001.
Слайд 9Сложение десятичных дробей путем поразрядного сложения, начиная с высших разрядов
Отдельно сложить
8,4 + 6,51 = ((8,4 + 6) + 0,5) + 0,01 = (14,4 + 0,5) + 0,01 = 14,9 + 0,01 = 14,91.
Слайд 10СПООБЫ БЫСТРОГО ВЫЧИТАНИЯ ЧИСЕЛ
Поразрядное вычитание
574 - 243 = (500 -
Если число единиц какого-либо разряда вычитаемого больше числа единиц того же разряда уменьшаемого, то последнее число единиц увеличивается на 10 путем заимствования одной единицы следующего высшего разряда уменьшаемого.
647 – 256 = (500 - 200) + ( 140 - 50 ) + ( 7 - 6) = 300 + 90 + 1 = 391
Слайд 11Вычитание с использованием свойств действий с числами
1358 – (158 + 78)
(973 +747) - 873 = (973 - 873) + 747 = 100 + 747 = 847;
5861 + (1414 – 884) = (5861 + 1414) - 884 = 7275 - 884 = 6391;
1093 - (1494 - 907) = (1093 + 907) = 2000 - 1494 = 506.
Слайд 12.
Вычитание путем уравнивания числа единиц последних разрядов уменьшаемого
67 - 48
453 - 316 = 453 – (313 + 3) = (453 - 313) - 3 = 140 - 3 = 137.
Слайд 13Вычитание путем округления уменьшаемого или вычитаемого или одновременно обоих
Если уменьшаемое и/или
713 - 65 = (700 + 13) - 65 = (700 - 65) + 13 = 635 + 13 = 648;
824 - 396 = 800 – (400 - 4) = (824 - 400) + 4 = 424 + 4 = 428;
395 – 98 = (400 – 5) – (100 – 2) = 400 – 100 – 5 + 2 = 297
Слайд 14. СПОСОБЫ БЫСТРОГО УМНОЖЕНИЯ ЧИСЕЛ
3.1 Умножение на 4, 8,16 и т.д
.
Чтобы
213 * 8 = (213 * 2) * 4= (426 * 2) * 2 = 852 * 2= 1704.
Слайд 15
3.2 Умножение на 5; 50; 0,5; 25; 2,5; 0,25; 125; 12,5;
Чтобы умножить число на 5, нужно умножить его на 10 и разделить на 2 .
138 5 = (138 10) : 2 = 1380 : 2 = 690.
Чтобы умножить число на 50, нужно умножить его на 100 и полученное произведение разделить на 2 .
87 50 =(87100) : 2 = 4350.
Чтобы умножить число на 0,5, нужно разделить на 2 .
3600,5 = 360 : 2 = 180.
Чтобы умножить число на 25, нужно умножить его на 100 и полученное произведение разделить на 4.
34825 = 34800 : 4 = 8700
Слайд 16Чтобы умножить число на 2,5, нужно умножить его на 10 и
96*2,5=960:4=240
Слайд 17Чтобы умножить число на 0,25, нужно разделить его на 4.
Чтобы умножить число на 125, нужно умножить его на 1000 и разделить на 8.
32*125=32:8*1000=4000
Чтобы умножить число на 12,5, нужно умножить его на 100 и разделить на 8.
24*12,5=24:8*100=300
Чтобы умножить число на 1,25, нужно умножить его на 10 и разделить на 8.
64:1.25=64*10:8=640:8=80
Чтобы умножить число на 0,125, нужно разделить его на 8.
16.8*0.125=16.8:8=2,1
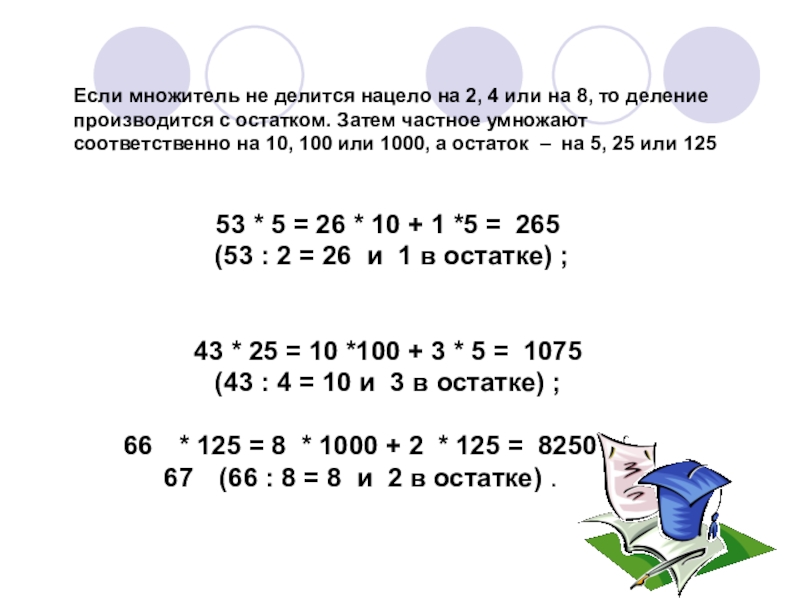
Если множитель не делится нацело на 2, 4 или на 8, то деление производится с остатком. Затем частное умножают соответственно на 10, 100 или 1000, а остаток – на 5, 25 или 125.
Слайд 1853 * 5 = 26 * 10 + 1 *5 =
(53 : 2 = 26 и 1 в остатке) ;
43 * 25 = 10 *100 + 3 * 5 = 1075
(43 : 4 = 10 и 3 в остатке) ;
* 125 = 8 * 1000 + 2 * 125 = 8250
(66 : 8 = 8 и 2 в остатке) .
Если множитель не делится нацело на 2, 4 или на 8, то деление производится с остатком. Затем частное умножают соответственно на 10, 100 или 1000, а остаток – на 5, 25 или 125
Слайд 193.3 Умножение на 1,5 и на 15.
Чтобы умножить число на 1,5,
Чтобы умножить число на 15, нужно исходное число умножить на 10 и прибавить половину полученного произведения.
24 * 1,5 = 24 + 12 = 36;
2)129 * 15 = 1290 + 645 = 1935.
Слайд 203.4 Умножение на 11
1 способ.
Чтобы число умножить на 11 , к
241 *11 = 2410 + 241 = 2651,
2 способ.
Следует “раздвинуть” цифры числа, умножаемого на 11, и в образовавшийся промежуток вписать сумму этих цифр, причем если эта сумма больше 9, то, как при обычном сложении, следует единицу перенести в старший разряд.
34 * 11 = 374, т.к. 3 + 4 =7, семерку помещаем между тройкой и четверкой,
68 * 11 = 748, т.к. 6 + 8 = 14, четверку помещаем между семеркой (шестерка плюс перенесенная единица) и восьмеркой.
Слайд 213.5 Умножение двузначного числа на 101 и на 10101.
Пожалуй, самое простое
1) 57 * 101 = 5757. 2) 89 * 10101 = 898989.
3.6 Умножение на 9, 99 и 999.
К первому множителю приписать столько нулей, сколько девяток во втором множителе, и из результата вычесть первый множитель
286 * 9 = 2860 – 286 = 2574;
23 * 99 = 2300 – 23 = 2277;
18 * 999 = 18000 – 18 = 17982.
Слайд 223.7 Применение распределительного закона умножения относительно сложения и вычитания к множителям,
8 * 318 = 8 * (300 + 0+8)= 2400 + 80 + 64 =2544;
2) 7 * 196 = 7 * (200 - 4) = 1400 – 28 = 1372.
Слайд 234. СПОСОБЫ БЫСТРОГО ДЕЛЕНИЯ ЧИСЕЛ
4.1 Последовательное деление
Если делитель является составным числом,
1)720 : 45 = (720 : 9) : 5 = 80 : 5 = 16 или
2) 9324 : 36 = ( 9324 : 3 ) : 12 = 3108 : 12 = 259.
4.2 Деление на 0,5; 5; 50 и 500
Чтобы число разделить на 0,5; 5; 50 или 500, надо это число разделить на 1; 10; 100 или 1000 соответственно, и затем результат умножить на 2.
1) 21600 : 50 = 21600 : 100 * 2 = 432.
2) 42400 : 5 = 42400 : 10 * 2 = 8480.
3) 214000 : 500 = 214000 : 1000 * 2 = 428.
4) 218 : 0,5 = 1218 * 2= 436.
Слайд 244.3 Деление на 25; 2,5; 0,25
Чтобы число разделить на 25,
12100 : 25 = 12100 : 100 * 4 = 484 .
2) 31 : 0,25 = 31 * 4 = 124 .
3) 240 : 2,5 = 240 : 10 * 4= 24 * 4 = 96
4.4 Деление на 125; 12,5; 1,25; 0,125
Чтобы число разделить на 125; 12,5; 1,25; 0,125, надо это число умножить на 8 и разделить на 1000; 100; 10; 1 соответственно (см. Приложение I).
1) 4000 : 12,5 = 4000 : 100 * 8 = 320. 2) 9000 : 125 = 9000 : 1000 * 8 = 72.
3) 18 : 1,25 = 144 : 10 * 8 = 14,4. 4) 11 : 0,125 = 11 * 8 = 88.
Слайд 255. Возведение в квадрат числа, оканчивающегося цифрой 5
Чтобы возвести в квадрат
952 = 9025; 1252 = 15625 .
9*10 12*13
Слайд 26
Практическая часть работы включала изучение динамики развития вычислительных навыков.
Были выдвинуты
с помощью приемов быстрого счета можно улучшить вычислительные навыки
невозможно улучшить вычислительные навыки с помощью приемов быстрого счета
Объект исследования - автор работы (ученица 6 класса).
Исследование включало:
изучение способов быстрого устного счета;
подбор материалов для тренинга;
проведение диагностики нашего объекта исследования;
разработка схем быстрого умножения и деления на 0,5; 5; 50;25; 2,5; 0,25; 125; 12,5; 1,25; 0,125; 9; 99; 999
6. Диагностика уровня вычислительных навыков
Слайд 27Для диагностики были составлены 4 блока однотипных упражнений, состоящих из 27
Диагностика проводилась по этапам:
I этап. «Нулевой замер». Проверялись имеющиеся навыки устного счета.
II этап. Изучение «хитрых» способов сложения и вычитания. Второй замер.
III этап. Ознакомление с новыми приемами умножения. Третий замер.
IV этап. Изучение способов деления. Четвертый замер.
Слайд 28Обработка результатов показала:
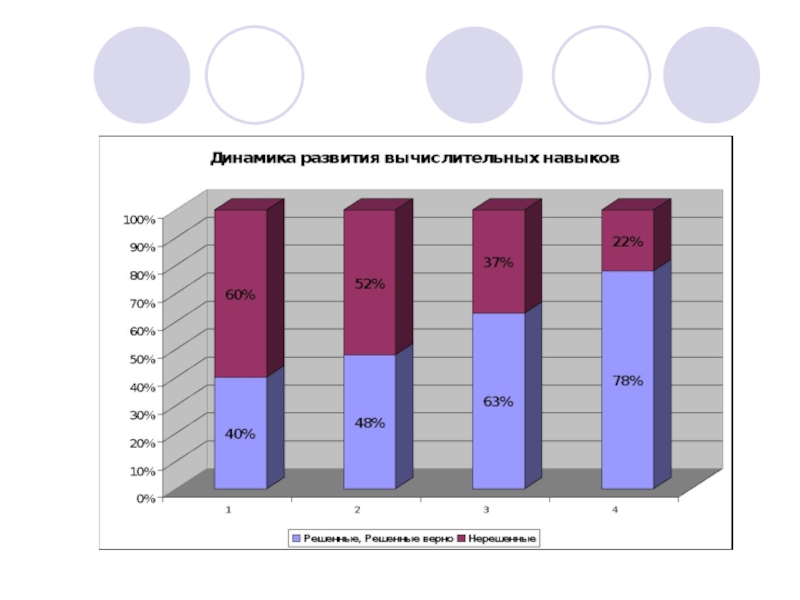
На начальном этапе было выполнено из 27 заданий 41%,
После изучения способов сложения и вычитания во 2 замере из 27 заданий было сделано 50%, где все задания выполнены верно, причем устно - 46% заданий, а столбиком 4% заданий.
Перед 3 замером были предложены новые приемы вычислений:
умножение чисел меньших 100 и 1000, близких к любому круглому двузначному или трехзначному числу, превышающих 100 и 1000, близких к круглому числу, когда дополнение одного числа является положительным, а другое отрицательно;
возведение в квадрат двузначных и трехзначных чисел меньших 100 и 1000, превышающих 100 и 1000.
Слайд 29На этом этапе выполнено из 27 заданий - 63%, все правильно,
Результат четвертого замера показал 78% выполнения всех заданий.
Из представленных диаграмм (см. Приложение II) видно, что от замера к замеру количество нерешенных заданий уменьшается, а решенных увеличивается, растет и число заданий, выполненных устно.
Таким образом, принимаем гипотезу о том, что можно улучшить вычислительные навыки с помощью приемов быстрого счета.
Для обучения приемам быстрого счета автором разработаны схемы умножения и деления (см. Приложение), которые будут использованы на факультативных занятиях.
Слайд 30
Из выше рассмотренного следует сделать выводы, что вычислительные навыки надо развивать и что развить их может каждый уважающий себя человек, будь то взрослый или ребенок, независимо от его математических способностей, хотя бы, для того чтобы не стать жертвой обмана в нашем сложном мире.
Слайд 31ЗАКЛЮЧЕНИЕ
Необходимым условием успешной работы, так или иначе связанной с вычислениями, является
В этом году мы продолжим практическую часть нашей работы на примере учащихся 6-х классов, обучив их приемам быстрого счета на элективных курсах по математике, и на основе полученных результатов проведем анализ динамики развития вычислительных навыков.
Счет является простым и легким делом только, когда владеешь особыми приемами и навыками. Каждый ученик может улучшить вычислительные навыки с использованием приемов быстрого счета. Наработка вычислительных навыков должна быть систематической, ежедневной, надо стремиться к тому, чтобы как можно больше освоить “хитрых” приемов.
В заключение подчеркнем, что устный счет развивает механическую память, быстроту реакции, умение сосредоточиться, а поиски и обоснование новых приемов служат формированию логических умений.
Слайд 34Литература
Гольштейн Д.Н. Техника быстрых вычислений. - М., Учпедгиз, 1948.
Перельман Я.И. Быстрый
Сорокин А.С. Техника счета. - М., Знание, 1976.
Математика в школе. - М., Педагогика, № 1, 1992.
Перельман Я.И. Живая математика. - Екатеринбург, Тезис, 1994.
Перельман Я.И. Занимательная алгебра. - Екатеринбург, Тезис, 1994.
Ткачева М.В. Домашняя математика. - М., Просвещение,1993.
Зайкин М.Н. Математический тренинг. - Москва, 1996.
Сивашинский И.Х. Задачи по математике для внеклассных занятий. – Москва «Просвещение», 1968.
Шарыгин И.Ф., Шевкин А.В. Задачи на смекалку.– Москва «Просвещение», 1996.