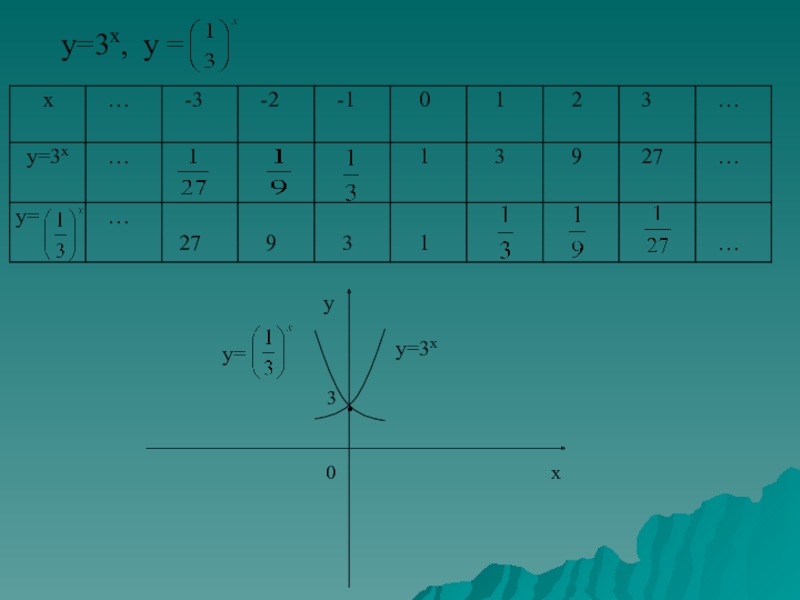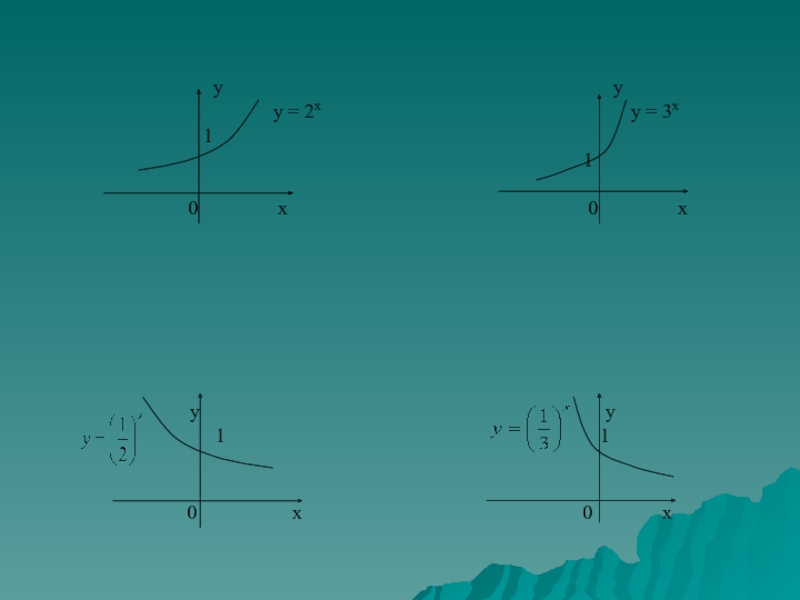часто
встречающиеся виды
трансцендентных функций,
прежде всего показательные,
открывают доступ ко
многим исследованиям.
Л.Эйлер.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Показательная и логарифмическая функция
Содержание
- 1. Презентация Показательная и логарифмическая функция
- 2. Показательная и логарифмическая функции И их применение в природе и технике.
- 3. Тема «Показательная и логарифмическая функция» является основополагающей
- 4. В природе целый ряд явлений, которые можно математически описать с помощью показательной и логарифмической функции
- 5. Рост народонаселения
- 6. Зависимость давления атмосферы от высоты над уровнем моря!
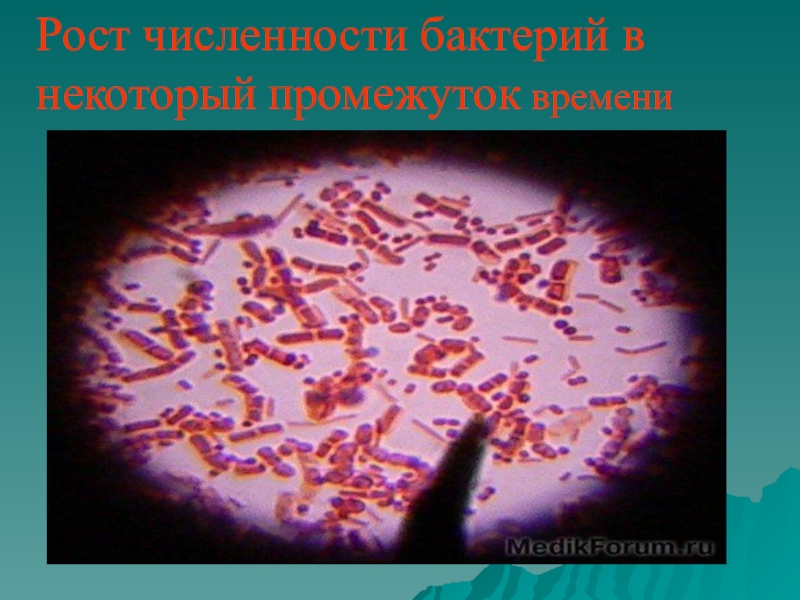
- 7. . . Рост численности бактерий в некоторый промежуток времени
- 8. В питательной среде бактерия кишечной палочки делится
- 9. Много трудных математических задач приходится решать в
- 10. Если не учитывать сопротивление воздуха и притяжение
- 11. Радиоактивный распад радия можно описать соотношением: m(t)=m(0)(0,9996)t,
- 12. Задача:Период полураспада плутония равен 140 суткам. Сколько
- 13. Как видите, во всех
- 14. Вот некоторые из Нобелевских лауреатов, получивших премию
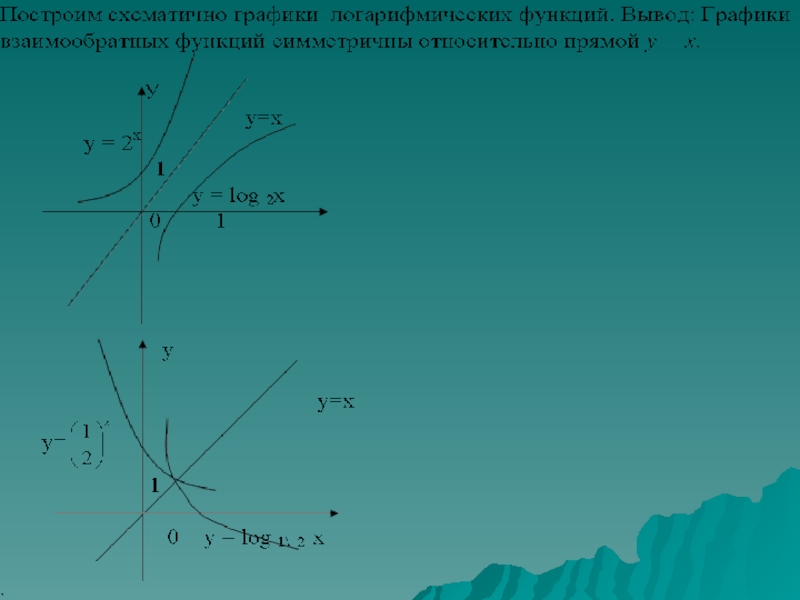
- 15. Графики обратных функций Y=X2 на промежутке от [0 до +∞) и Y=√X
- 16. Слайд 16
- 17. у=3х, у =у
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. . 1) у
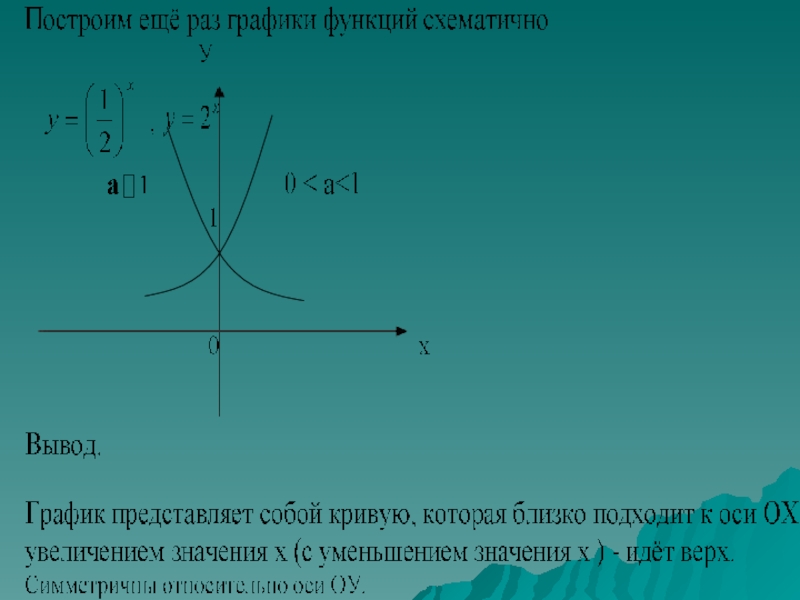
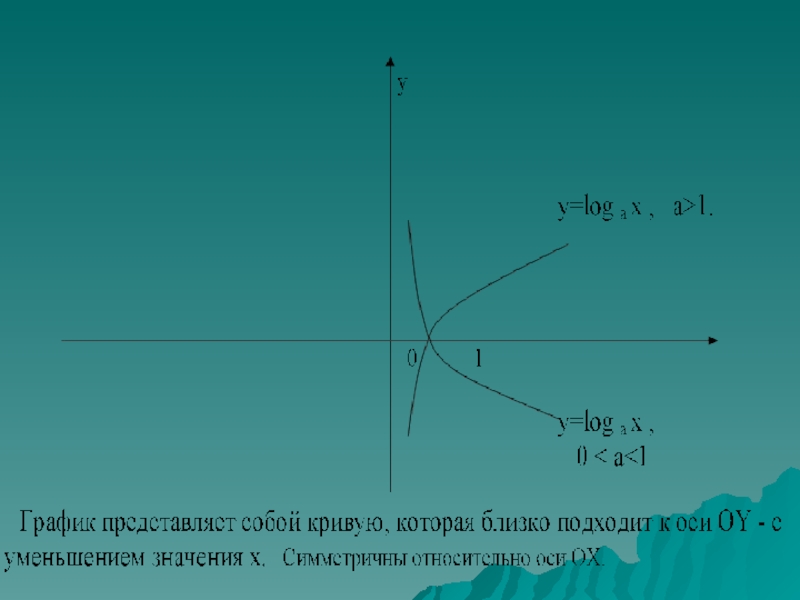
- 23. Подведём итог темы: График функции Область - является множество действительных чисел (R). -является Область
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Спасибо за урок
Показательная и логарифмическая функции И их применение в природе и технике.
Слайд 1Презентация по теме: «Показательная и логарифмическая функции. Свойства и графики».
Некоторые наиболее
Слайд 3Тема «Показательная и логарифмическая функция» является основополагающей при изучении таких тем,
как «Уравнения и неравенства, содержащие эти функции»,«Производная показательной, логарифмической функции», «Термодинамика», «Электромагнетизм», «Ядерная физика», «Колебания», используется для решения некоторых задач судовождения.
Слайд 4В природе целый ряд явлений, которые можно математически описать с помощью
показательной и логарифмической функции
Слайд 8В питательной среде бактерия кишечной палочки делится каждую минуту. Понятно, что
общее число бактерий за каждую минуту удваивается. Если в начале процесса была одна бактерия, то через х минут их число (N) станет равной 2х , т.е.
N(х) = 2х.
Слайд 9Много трудных математических задач приходится решать в теории межпланетных путешествий. Одной
из них является задача об определении массы топлива, необходимого для того, чтобы придать ракете нужную скорость v. Эта масса М зависит от массы m самой ракеты (без топлива) и от скорости v0, с которой продукты горения вытекают из ракетного двигателя.
Слайд 10Если не учитывать сопротивление воздуха и притяжение Земли, то масса топлива
определиться формулой: M=m(ev/v0-1) (формула К.Э.Циалковского). Например, для того чтобы ракете с массой 1,5 т придать скорость 8000 м/с, надо при скорости истечения газов 2000 м/с взять примерно 80 т топлива.
Слайд 11Радиоактивный распад радия можно описать соотношением: m(t)=m(0)(0,9996)t,
m(0)-первоначальное количество радия в
граммах;
m(t)- количество радия , которое останется через t лет после начала распада радия. Через сколько лет количество радия уменьшится вдвое?
m(t)=1\2 m(0)-уменьшится вдвое.
m(0)(0,9996)t=1\2 m(0), (0,9996)t=1\2,t= log0,9996 0,5=1600(лет). Таким образом, количество радия уменьшится вдвое через каждые 1600 лет.
m(t)- количество радия , которое останется через t лет после начала распада радия. Через сколько лет количество радия уменьшится вдвое?
m(t)=1\2 m(0)-уменьшится вдвое.
m(0)(0,9996)t=1\2 m(0), (0,9996)t=1\2,t= log0,9996 0,5=1600(лет). Таким образом, количество радия уменьшится вдвое через каждые 1600 лет.
Слайд 12Задача:
Период полураспада плутония равен 140 суткам. Сколько плутония останется через 10
лет, если его начальная масса равна 8г ?
Слайд 13Как видите, во всех
приведенных выше исследованиях использовалась показательная и логарифмическая функции.
Слайд 14Вот некоторые из Нобелевских лауреатов, получивших премию за исследования в области
физики с использованием показательной и логарифмической функции:
Пьер Кюри - 1903 г.
Ричардсон Оуэн - 1928 г.
Игорь Тамм - 1958 г.
Альварес Луис - 1968 г.
Альфвен Ханнес - 1970 г.
Вильсон Роберт Вудро - 1978 г.
Пьер Кюри - 1903 г.
Ричардсон Оуэн - 1928 г.
Игорь Тамм - 1958 г.
Альварес Луис - 1968 г.
Альфвен Ханнес - 1970 г.
Вильсон Роберт Вудро - 1978 г.
Слайд 22
.
1) у
2) у 3) у 4) у
0 1 х 0 х 0 х 0 Х
Задание №1
а) укажите соответствие данных функций и их графиков.
б) назовите свойства этих функций .
Слайд 23Подведём итог темы:
График функции
Область
- является множество действительных чисел
(R).
-является
Область
