- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
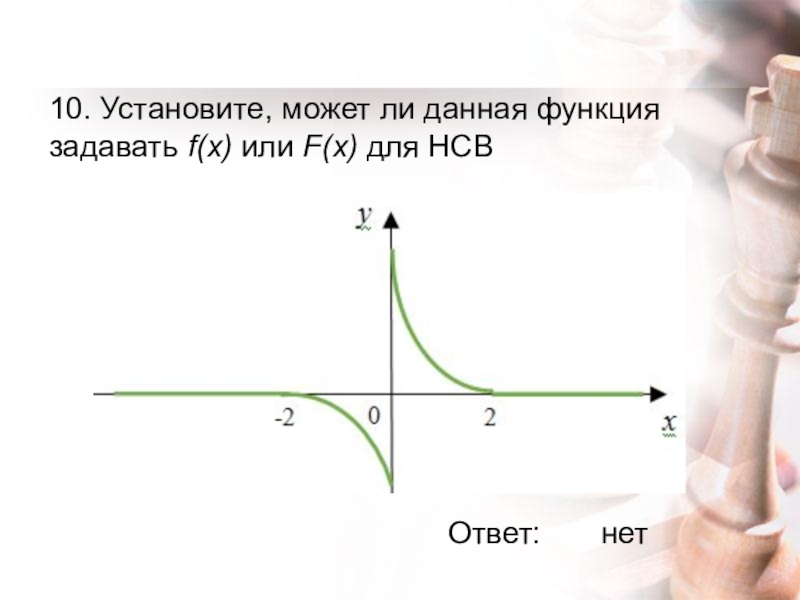
- МХК
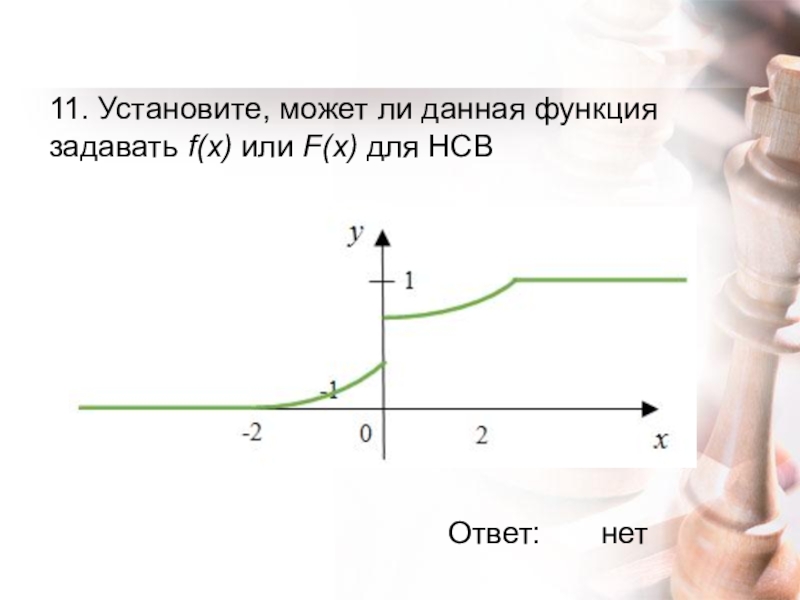
- Немецкий язык
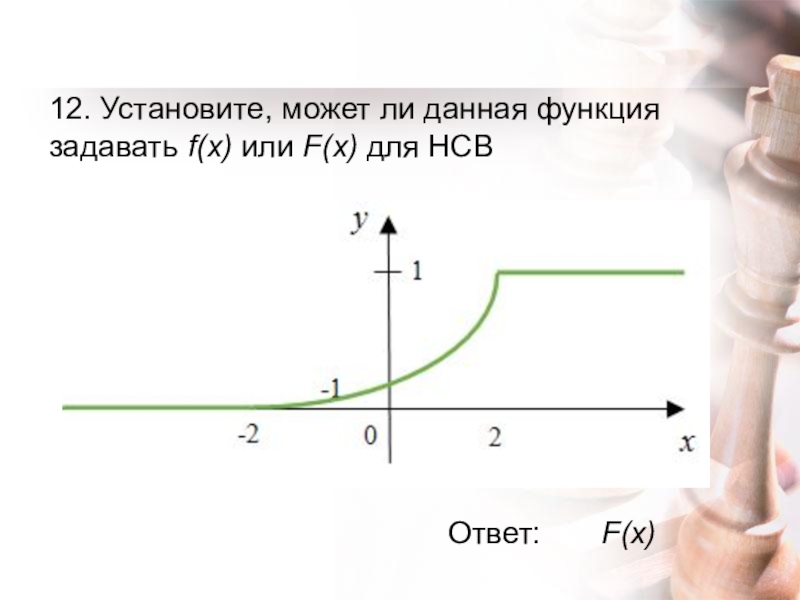
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теории вероятностей на тему Непрерывные случайные величины (СПО)
Содержание
- 1. Презентация по теории вероятностей на тему Непрерывные случайные величины (СПО)
- 2. План:Понятие НСВЗадание НСВИнтегральная функция распределения НСВПрактическая работаЛитература
- 3. Понятие случайной величины. Случайная величина - величина,
- 4. Понятие НСВ. Случайная величина, принимающая все значения
- 5. Задание НСВ. НСВ задаётся функцией плотности вероятности
- 6. Что наиболее вероятно:Случайная величина примет значения от
- 7. Пример 1. Проверьте корректность задания: и определите
- 8. Интегральная функция распределения Данную функцию можно интерпретировать
- 9. Пример 2. Интегральная функция распределения задана выражением:
- 10. Пример 3. По известной функции плотности вероятности f(x) найдите интегральную функцию распределения F(х), если ПримерПроверка решения:F(х)=
- 11. А теперь попробуйте свои силы в выполнении практических заданий.Желаю успеха!
- 12. ИЗ ДАННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН НЕПРЕРЫВНЫМИ ЯВЛЯЮТСЯдиаметр
- 13. 2. ФУНКЦИЯ ПЛОТНОСТИ ВЕРОЯТНОСТИ МОЖЕТ ПРИНИМАТЬ ЗНАЧЕНИЯ[-1; 0][0; 1][-1; 1][0; +∞)(-∞; +∞)Ответ:D
- 14. 3. ИНТЕГРАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МОЖЕТ ПРИНИМАТЬ ЗНАЧЕНИЯ[-1; 0][0; 1][-1; 1][0; +∞)(-∞; +∞)Ответ:В
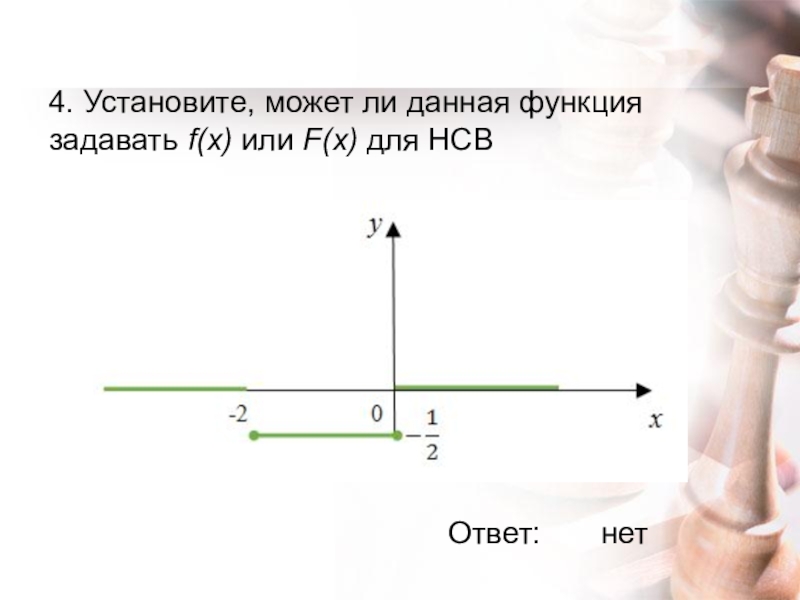
- 15. 4. Установите, может ли данная функция задавать f(x) или F(x) для НСВ Ответ:нет
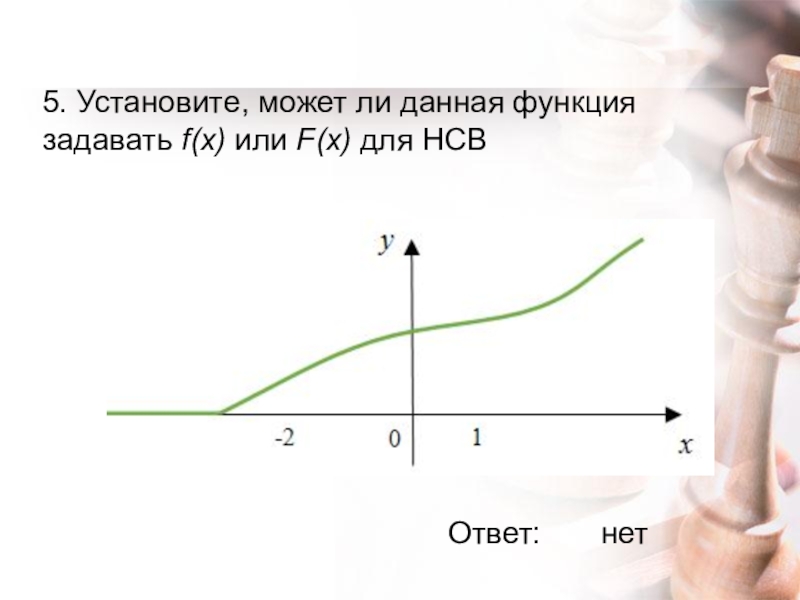
- 16. 5. Установите, может ли данная функция задавать f(x) или F(x) для НСВ Ответ:нет
- 17. 6. Установите, может ли данная функция задавать
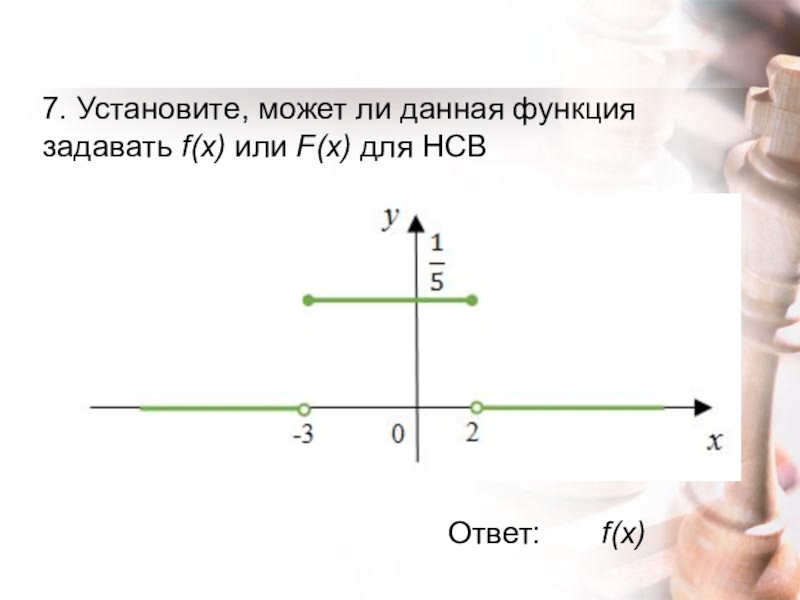
- 18. 7. Установите, может ли данная функция задавать f(x) или F(x) для НСВ Ответ:f(x)
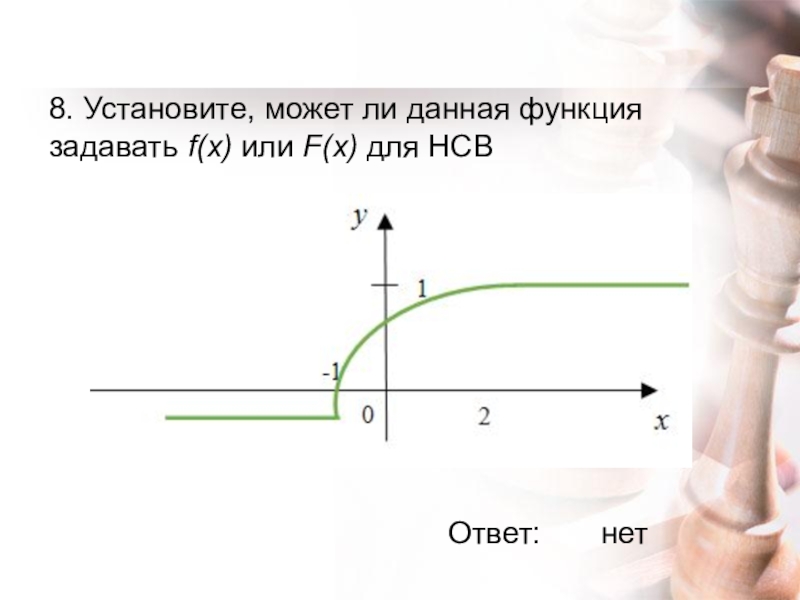
- 19. 8. Установите, может ли данная функция задавать f(x) или F(x) для НСВ Ответ:нет
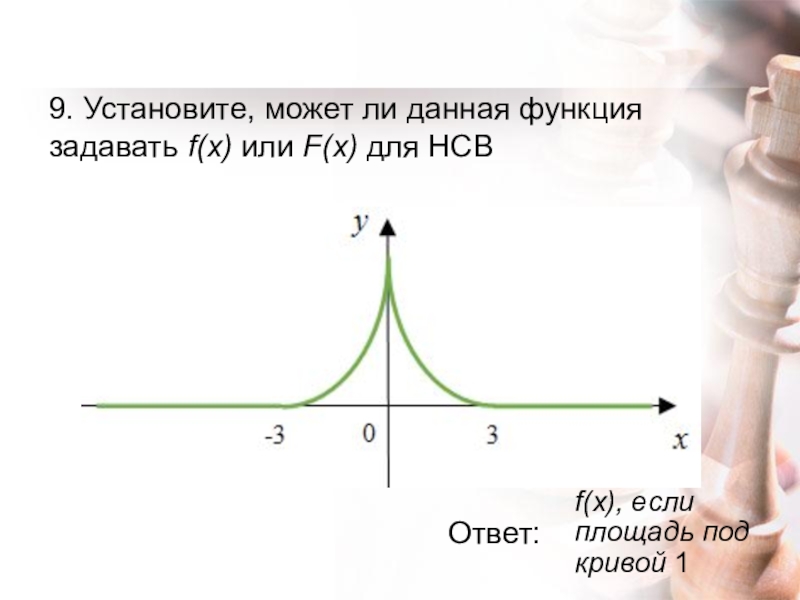
- 20. 9. Установите, может ли данная функция задавать
- 21. 10. Установите, может ли данная функция задавать f(x) или F(x) для НСВ Ответ:нет
- 22. 11. Установите, может ли данная функция задавать f(x) или F(x) для НСВ Ответ:нет
- 23. 12. Установите, может ли данная функция задавать f(x) или F(x) для НСВ Ответ:F(x)
- 24. 13. ДЛЯ НСВ, ЗАДАННОЙ ФУНКЦИЕЙ ПЛОТНОСТИ ВЕРОЯТНОСТИВЕРОЯТНОСТЬ
- 25. 14. ИНТЕГРАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ НСВ ИМЕЕТ ВИД:ВЕРОЯТНОСТЬ
- 26. 15. ДЛЯ ИНТЕГРАЛЬНОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ФУНКЦИЯ ПЛОТНОСТИ ВЕРОЯТНОСТИ ИМЕЕТ ВИДОтвет:
- 27. 16. ДЛЯ ФУНКЦИИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ИНТЕГРАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ИМЕЕТ ВИДОтвет:
- 28. Спасибо за внимание!Литература:Спирина, М.С. Теория вероятностей и
Слайд 1Автор: Шереметьева Н.В.,
преподаватель математики
ГПОУ ЯО Ярославский градостроительный колледж
НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Слайд 2План:
Понятие НСВ
Задание НСВ
Интегральная функция распределения НСВ
Практическая работа
Литература
Слайд 3Понятие случайной величины
.
Случайная величина - величина, которая в результате опыта
Случайная величина -
Случайная величина называется дискретной, если
в результате опыта она принимает числовые значения, которые можно перечислить или поставить им в соответствие элементы счётного множества
Испытание: в случайный момент времени прийти на остановку автобуса, который ходит с интервалом 10 минут.
Х – время ожидания автобуса.
0
0,5
2/3
1
1,4
2
…
10
перечислить невозможно!!!
0
0
0
0
0
0
0
0
невероятно!!!
Слайд 4Понятие НСВ
.
Случайная величина, принимающая все значения из некоторого интервала (их
Можно ли задать НСВ законом распределения?
Попробуем задать НСВ графически:
10
Пусть мерой вероятности попадания значений в интервал (a; b) будет площадь соответствующей криволинейной трапеции
Например, Р(0 2 S1 Полученную функцию назовём функцией плотности вероятности f(x).
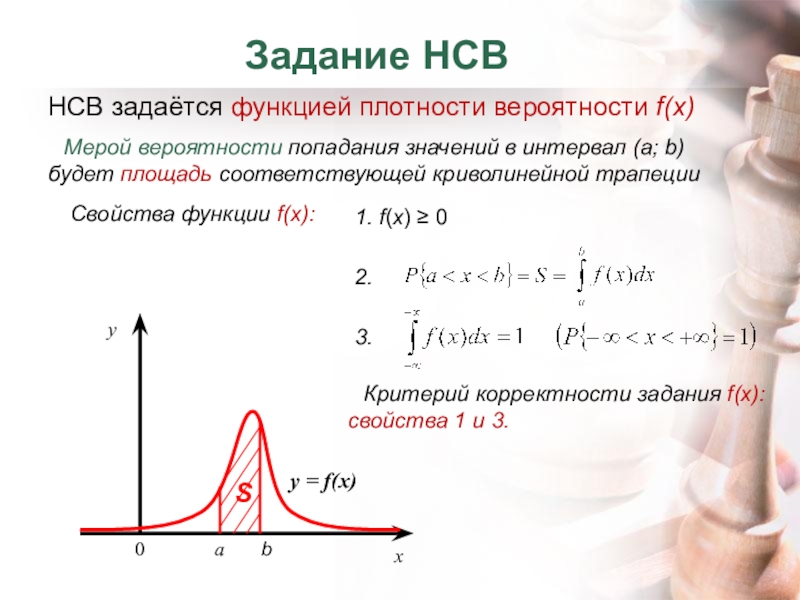
Слайд 5Задание НСВ
.
НСВ задаётся функцией плотности вероятности f(x)
а
Свойства функции f(x):
b
Мерой
1. f(x) ≥ 0
у = f(x)
2.
S
3.
Критерий корректности задания f(x): свойства 1 и 3.
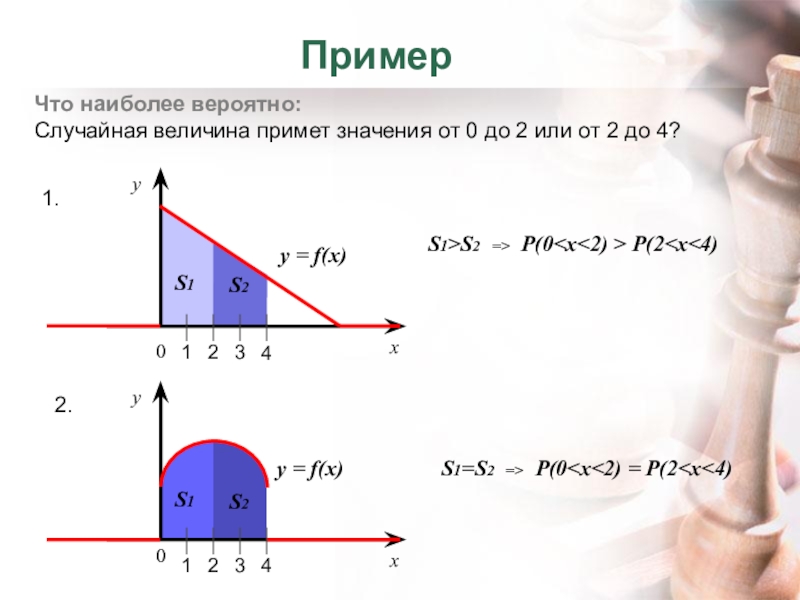
Слайд 6Что наиболее вероятно:
Случайная величина примет значения от 0 до 2 или
Пример
у = f(x)
1
2
3
4
2.
у = f(x)
1
2
3
4
1.
S1
S2
S1>S2 => P(0 S1=S2 => P(0 S1 S2
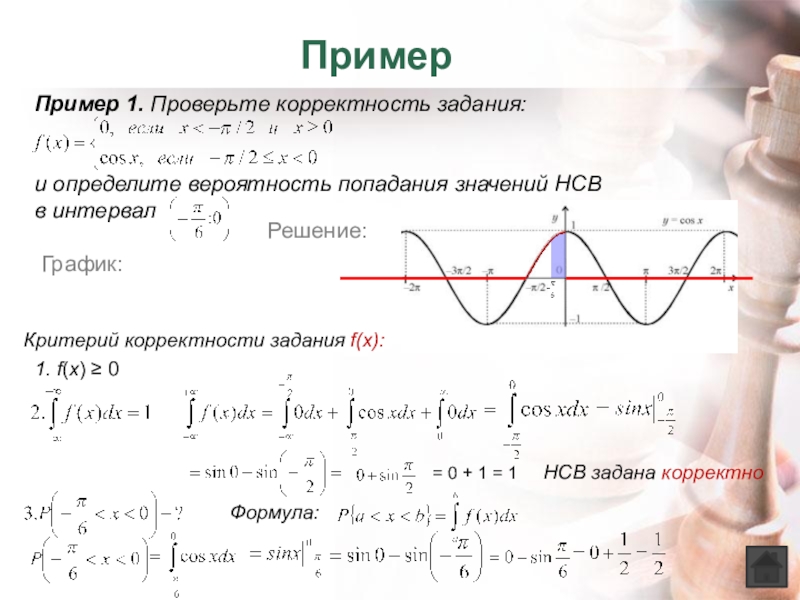
Слайд 7Пример 1. Проверьте корректность задания:
и определите вероятность попадания значений НСВ
в интервал
Пример
Решение:
График:
Критерий корректности задания f(x):
1. f(x) ≥ 0
= 0 + 1 = 1
НСВ задана корректно
Формула:
Слайд 8Интегральная функция распределения
Данную функцию можно интерпретировать как функцию накопления вероятностей.
Свойства
1.
2. F(x) – неубывающая функция
3.
4.
F(x) = P(X < x)
Связь f(x) и F(x):
F(x) – первообразная для f(x)
f(x) = F’(x)
F(x) =
Случайная величина Х является непрерывной, если ее интегральная функция распределения F(x) = P{X < x} непрерывна и дифференцируема, за исключением, быть может, конечного числа точек.
Слайд 9Пример 2. Интегральная функция распределения задана выражением:
F(х)=
а) найдите f(x),
б) докажите корректность задания НСВ,
в) вычислите Р(0,6 1)
г) постройте графики F(х) и f(x), отметьте на графиках вероятность, найденную в пункте (в).
Пример
Проверка решения:
Р(0,6 1) = F(1) - F(0,6) = 12 – 0,62 = 1 – 0,36 = 0,64
Слайд 10Пример 3. По известной функции плотности вероятности f(x) найдите интегральную функцию
Пример
Проверка решения:
F(х)=
Слайд 12 ИЗ ДАННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН НЕПРЕРЫВНЫМИ ЯВЛЯЮТСЯ
диаметр наудачу взятой монеты
скорость
число выпавших очков при подбрасывании двух игральных кубиков
количество орлов при подбрасывании 5 монет
масса наудачу взятой монеты
Ответ:
A, B, E
Слайд 132. ФУНКЦИЯ ПЛОТНОСТИ ВЕРОЯТНОСТИ МОЖЕТ ПРИНИМАТЬ ЗНАЧЕНИЯ
[-1; 0]
[0; 1]
[-1; 1]
[0; +∞)
(-∞;
Ответ:
D
Слайд 143. ИНТЕГРАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МОЖЕТ ПРИНИМАТЬ ЗНАЧЕНИЯ
[-1; 0]
[0; 1]
[-1; 1]
[0; +∞)
(-∞;
Ответ:
В
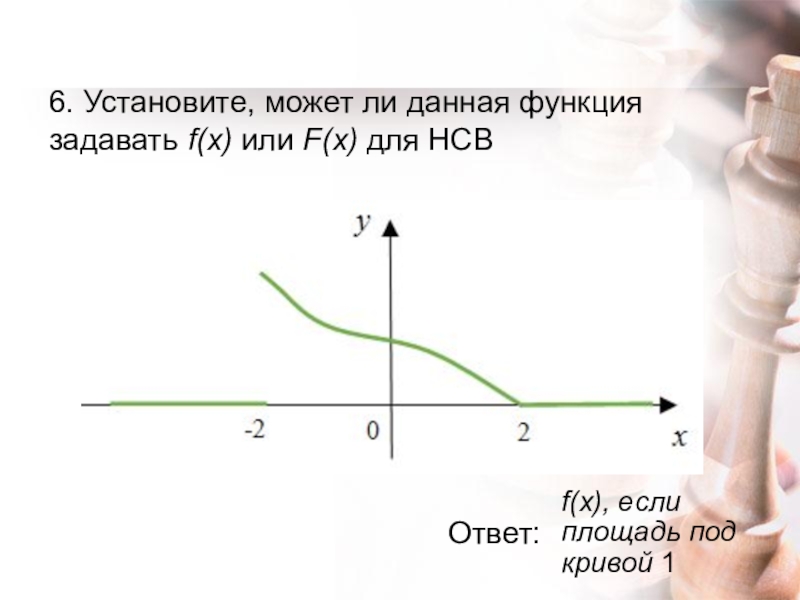
Слайд 176. Установите, может ли данная функция задавать f(x) или F(x) для
Ответ:
f(x), если площадь под кривой 1
Слайд 209. Установите, может ли данная функция задавать f(x) или F(x) для
Ответ:
f(x), если площадь под кривой 1
Слайд 2413. ДЛЯ НСВ, ЗАДАННОЙ ФУНКЦИЕЙ ПЛОТНОСТИ ВЕРОЯТНОСТИ
ВЕРОЯТНОСТЬ ТОГО, ЧТО СЛУЧАЙНАЯ ВЕЛИЧИНА
Ответ:
0,5
Слайд 2514. ИНТЕГРАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ НСВ ИМЕЕТ ВИД:
ВЕРОЯТНОСТЬ ТОГО, ЧТО СЛУЧАЙНАЯ ВЕЛИЧИНА
Ответ:
0,2
Слайд 28Спасибо за внимание!
Литература:
Спирина, М.С. Теория вероятностей и математическая статистика [Текст]: учебник
Спирина, М.С. Теория вероятностей и математическая статистика [Текст]: сборник задач. Учебное пособие / М.С. Спирина, П.А. Спирин. - 2-е изд., стер. - М: Изд. центр «Академия», 2018. – 192 с. - (Среднее профессиональное образование).









![Презентация по теории вероятностей на тему Непрерывные случайные величины (СПО) 2. ФУНКЦИЯ ПЛОТНОСТИ ВЕРОЯТНОСТИ МОЖЕТ ПРИНИМАТЬ ЗНАЧЕНИЯ[-1; 0][0; 1][-1; 1][0; +∞)(-∞; +∞)Ответ:D 2. ФУНКЦИЯ ПЛОТНОСТИ ВЕРОЯТНОСТИ МОЖЕТ ПРИНИМАТЬ ЗНАЧЕНИЯ[-1; 0][0; 1][-1; 1][0; +∞)(-∞; +∞)Ответ:D](/img/thumbs/2359b6095647007296e071190bd0afbe-800x.jpg)
![Презентация по теории вероятностей на тему Непрерывные случайные величины (СПО) 3. ИНТЕГРАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МОЖЕТ ПРИНИМАТЬ ЗНАЧЕНИЯ[-1; 0][0; 1][-1; 1][0; +∞)(-∞; +∞)Ответ:В 3. ИНТЕГРАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МОЖЕТ ПРИНИМАТЬ ЗНАЧЕНИЯ[-1; 0][0; 1][-1; 1][0; +∞)(-∞; +∞)Ответ:В](/img/thumbs/aa24c9d2cb35e85197ae3f670b6b3b06-800x.jpg)




![Презентация по теории вероятностей на тему Непрерывные случайные величины (СПО) Спасибо за внимание!Литература:Спирина, М.С. Теория вероятностей и математическая статистика [Текст]: учебник Спасибо за внимание!Литература:Спирина, М.С. Теория вероятностей и математическая статистика [Текст]: учебник / М.С. Спирина, П.А. Спирин. -](/img/thumbs/ba8c0aef93a1055bc54f2161e943993a-800x.jpg)





