- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Комбинаторика.Бином Ньютона
Содержание
- 1. Презентация по математике на тему Комбинаторика.Бином Ньютона
- 2. Самый простой метод решения комбинаторных задач –
- 3. Полный перебор может осуществляться с помощью деревьевС
- 4. Полный перебор может осуществляться с помощью таблиц
- 5. Задача. В футбольном турнире участвуют несколько команд.
- 6. При большом количестве имеющихся элементов полный перебор
- 7. Задача 1. Сколько различных двузначных чисел можно
- 8. Основные задачи комбинаторикиОсновными задачами комбинаторики считаются следующие:
- 9. ПерестановкиПерестановками из n элементов называются соединения, которые
- 10. Вычислить: 7! 2) 8!
- 11. Задача.Сколькими способами можно расставить на полке семь
- 12. Задача.Имеются 10 различных книг, три из которых
- 13. Размещения Число всех выборов n элементов
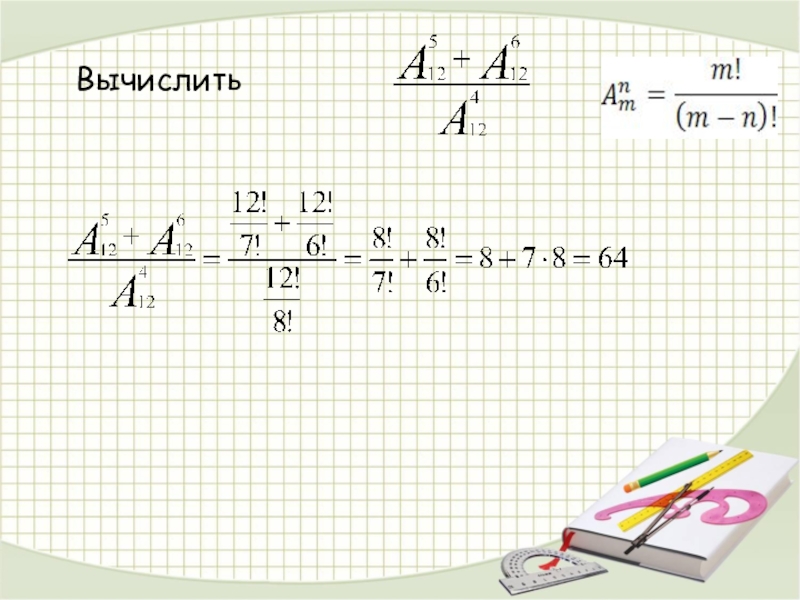
- 14. Вычислить
- 15. Задача. Решить уравнение:Решение:
- 16. Слайд 16
- 17. РазмещенияЗадача 2. Сколькими способами могут занятьI, II,
- 18. Задача 4 . Сколькими способами можно обозначить
- 19. Задача.Сколько существует трехзначных чисел, в которых цифры
- 20. Задача : Из пяти шахматистов для участия
- 21. СочетанияЧисло всех выборов n элементов из m
- 22. Слайд 22
- 23. СочетанияЗадача 2. Сколькими способами можно составить
- 24. Задача 4. Сколько существует способов выбора трёх
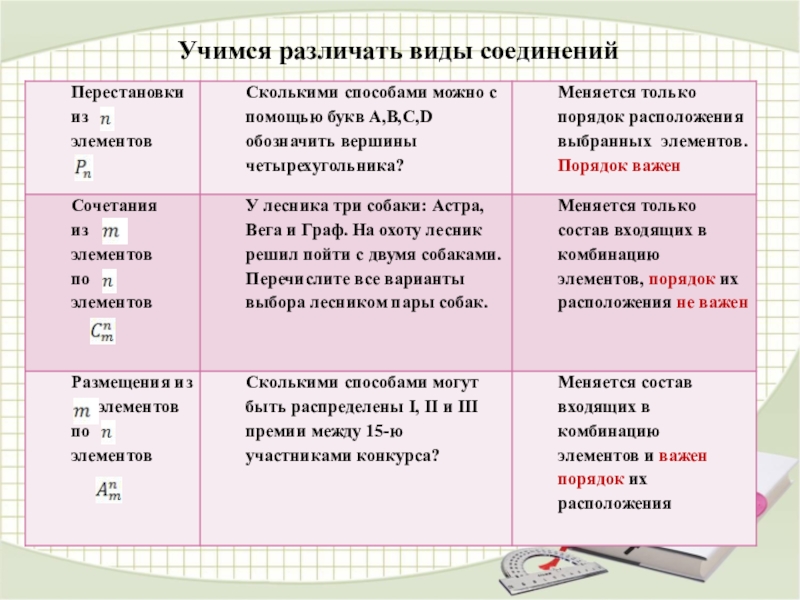
- 25. Учимся различать виды соединений
- 26. Треугольник Паскаля. Числа имеют очень красивую и
- 27. Треугольник Паскаля. Правило записи треугольника легко запомнить: Каждое
- 28. Треугольник Паскаля
- 29. Бином Ньютона. Как оказалось, треугольник Паскаля
- 30. Бином Ньютона. Выпишем для наглядности все наши
- 31. Бином Ньютона Бином Ньютона – это
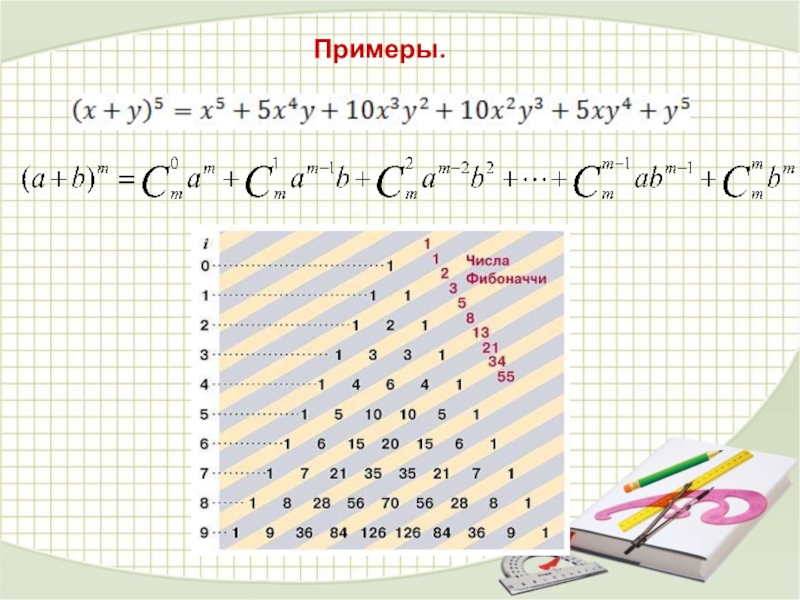
- 32. Примеры.
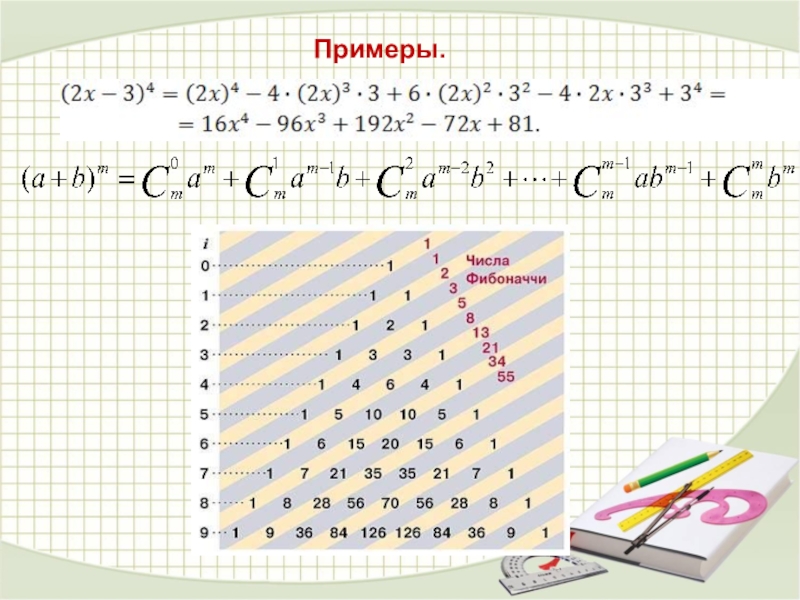
- 33. Примеры.
- 34. Бином Ньютона. Пример. Раскрыть скобки: а)
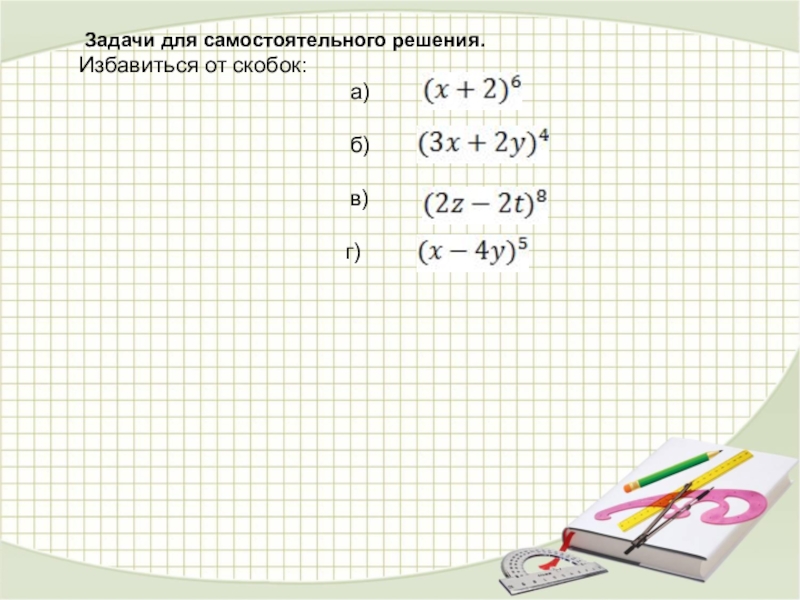
- 35. Задачи для самостоятельного решения. Избавиться от скобок:
- 36. Проверь себя1. Сколькими способами 4 вора могут
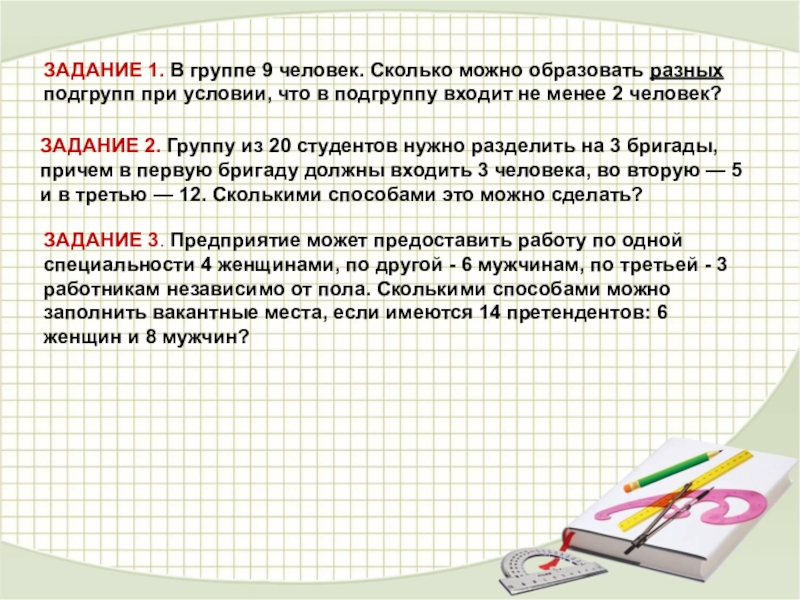
- 37. ЗАДАНИЕ 1. В группе 9 человек. Сколько
- 38. Решить уравнениеОтвет: 28
- 39. РЕШЕНИЕ ЗАДАЧ№ 1.Вычислите: № 2. В классе
- 40. Задача 1. Сколько различных двухзначных чисел можно
- 41. ЛитератураАлгебра и начала математического анализа 11 класс,
Слайд 2Самый простой метод решения комбинаторных задач – перебор всех возможных вариантов
Подсчитать
Ответ:10 (а, б, в, ж, и, к, о, с, у, я)
Перечислить виды: 1)треугольников, 2)четырехугольников.
Ответ:1)равносторонний, равнобедренный, разносторонний; остроугольный, прямоугольный, тупоугольный.
2) параллелограмм, прямоугольник, ромб, квадрат, трапеция.
В магазине продают бейсболки трех цветов: синие, красные и черные. Ваня и Андрей покупают себе по одной. Сколько существует различных вариантов покупки?
Ответ:9 вариантов.
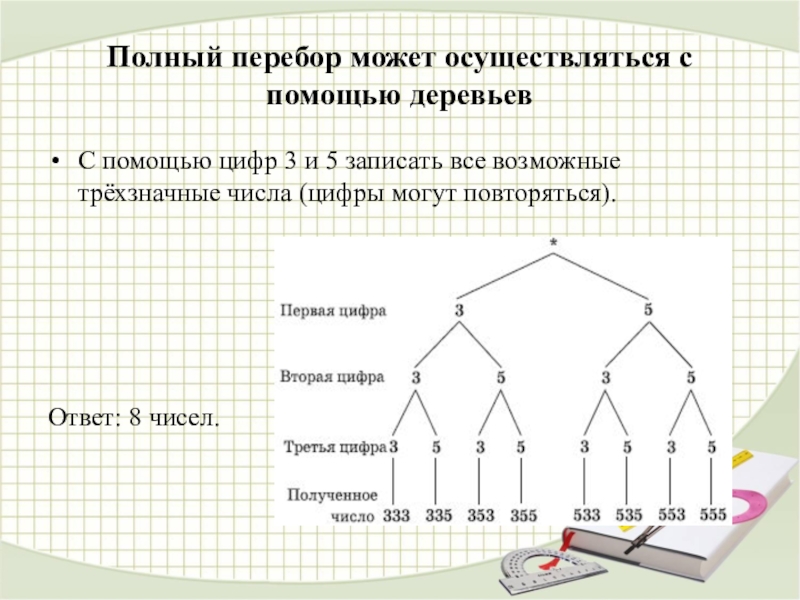
Слайд 3Полный перебор может осуществляться с помощью деревьев
С помощью цифр 3 и
Ответ: 8 чисел.
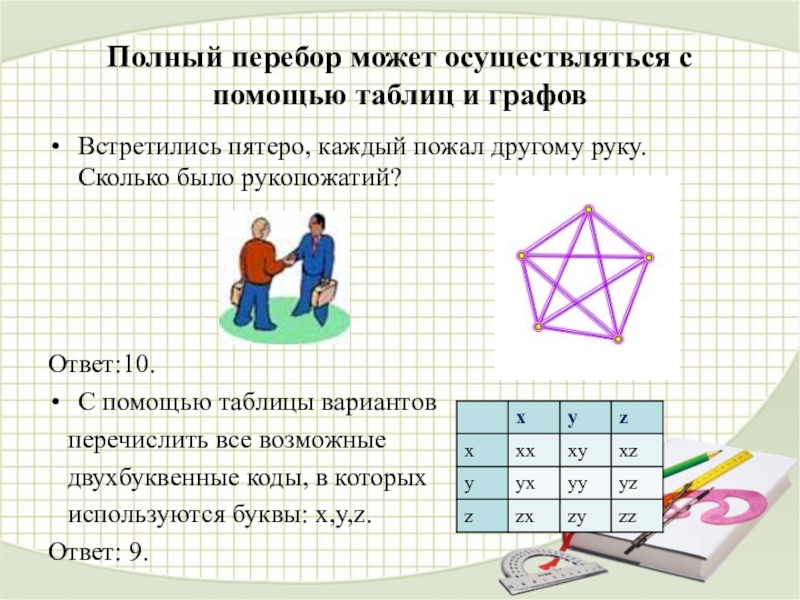
Слайд 4Полный перебор может осуществляться с помощью таблиц и графов
Встретились пятеро, каждый
Ответ:10.
С помощью таблицы вариантов
перечислить все возможные
двухбуквенные коды, в которых
используются буквы: x,y,z.
Ответ: 9.
Слайд 5Задача.
В футбольном турнире участвуют несколько команд. Оказалось, что все они
Слайд 6При большом количестве имеющихся элементов полный перебор затруднителен. Правило произведения позволяет
Сформулируем это правило.
Правило произведения
Если существует n вариантов выбора
первого элемента и для каждого из них имеется
m вариантов выбора второго элемента, то существует
nm различных пар с выбранными первым и
вторым элементами.
Слайд 7Задача 1. Сколько различных двузначных чисел можно записать с помощью цифр
Ответ: 4∙5 = 20.
Задача 2. В кафе имеются 3 первых блюда, 5 вторых и 2 третьих. Сколькими способами посетитель кафе может выбрать обед, состоящий из первого, второго и третьего блюд?
Ответ: 3∙5∙2 = 30.
Задача 3. Пётр решил пойти на новогодний карнавал в костюме мушкетёра. В ателье проката ему предложили на выбор различные по цвету и фасону предметы: 5 пар брюк, 6 камзолов, 3 шляпы, 2 пары сапог. Сколько различных карнавальных костюмов он может составить из этих предметов?
Ответ: 5∙6∙3∙2 = 180.
Слайд 8Основные задачи комбинаторики
Основными задачами комбинаторики считаются следующие:
составление упорядоченных множеств
составление подмножеств данного множества (сочетания)
составление упорядоченных подмножеств данного множества (размещения).
Чтобы отличать задачи на подсчёт числа размещений от задач на подсчёт числа сочетаний, определим, важен или нет порядок в следующих выборках:
а) судья хоккейного матча и его помощник;
б) три ноты в аккорде;
в) «Шесть человек останутся убирать класс!»
г) две серии для просмотра из многосерийного фильма.
Ответ: а)да; б)нет; в)нет; г)да.
Слайд 9Перестановки
Перестановками из n элементов называются соединения, которые состоят из n элементов
Permutation (фр.) – перестановка.
Задача. Сколькими способами можно расположить в столбик три детали конструктора, различающиеся по цвету?
Слайд 10Вычислить:
7! 2) 8! 3) 6!-5!
Определение: Произведение подряд идущих первых n натуральных чисел обозначают n! и называют «эн факториал». Принято считать, что 0! = 1
Задача.
В семье – 6 человек, и за столом в кухне стоят 6 стульев. Семья решила каждый вечер, ужиная рассаживаться на эти стулья по – новому. Сколько дней члены семьи смогут осуществлять задуманное?
Слайд 11Задача.
Сколькими способами можно расставить на полке семь различных книг?
Решение:
Число таких
т.е. P7 = 7! = 1 · 2 · 3 · … · 7 =
Ответ: 5040.
Слайд 12Задача.
Имеются 10 различных книг, три из которых – справочники. Сколькими способами
Решение:
Т.к. в справочники должны стоять рядом, то будем рассматривать их как одну книгу. Тогда на полке надо расставить 10 – 3+1=8 книг. Это можно сделать P8 способами. Для каждой из полученных комбинаций можно сделать P3 перестановок справочников. Поэтому число способов расположения книг на полке равно произведению:
P8 · P3 = 8! · 3! = 40320 · 6 =
Ответ: 241920.
Слайд 13Размещения
Число всех выборов n элементов из m данных с
Обозначают:
Слайд 17Размещения
Задача 2. Сколькими
способами могут занять
I, II, III места 8 участниц
финального
дистанции 100 м?
Ответ: 336.
Задача 1. Сколькими способами можно изготовить трёхцветный флаг с горизонтальными полосами, если имеется материал 7 различных цветов?
Ответ: 210.
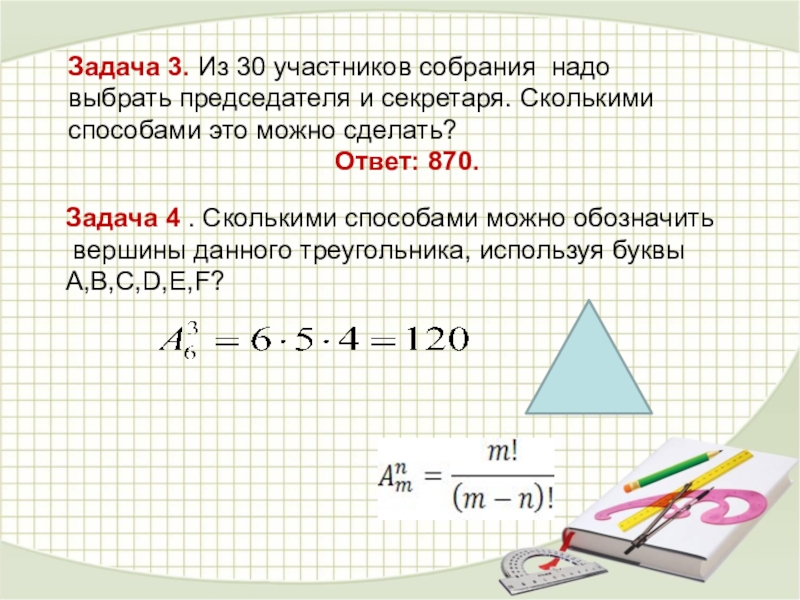
Слайд 18Задача 4 . Сколькими способами можно обозначить
вершины данного треугольника, используя
А,В,С,D,E,F?
Задача 3. Из 30 участников собрания надо
выбрать председателя и секретаря. Сколькими
способами это можно сделать?
Ответ: 870.
Слайд 19Задача.
Сколько существует трехзначных чисел, в которых цифры различные и нечетные.
Решение:
Нечётных цифр
Ответ: 60.
Слайд 20Задача : Из пяти шахматистов для участия в турнире нужно выбрать
Решение: Из пяти шахматистов можно составить пар
Но из этих пар надо выбрать только те, которые различаются лишь составом участников, таких пар в 2 раза меньше, т.е.
При решении этой задачи из 5 человек были образованы пары – соединения по 2 человека, которые отличались друг от друга только составом.
Такие соединения называют сочетаниями.
Слайд 21Сочетания
Число всех выборов n элементов из m данных без учёта порядка
Обозначают:
Слайд 23Сочетания
Задача 2. Сколькими способами можно составить
девяти имеющихся?
Ответ: 84.
Задача 3. В классе учатся 16 мальчиков и 12 девочек. Сколькими способами можно выделить 4 мальчиков и 3 девочек для уборки территории?
Ответ:
Задача 1. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
Ответ: 21.
Слайд 24Задача 4. Сколько существует способов выбора трёх карт из колоды в
Решение: Изъятые из колоды 3 карты без учета порядка их расположения в наборе являются сочетаниями из 36 по 3.
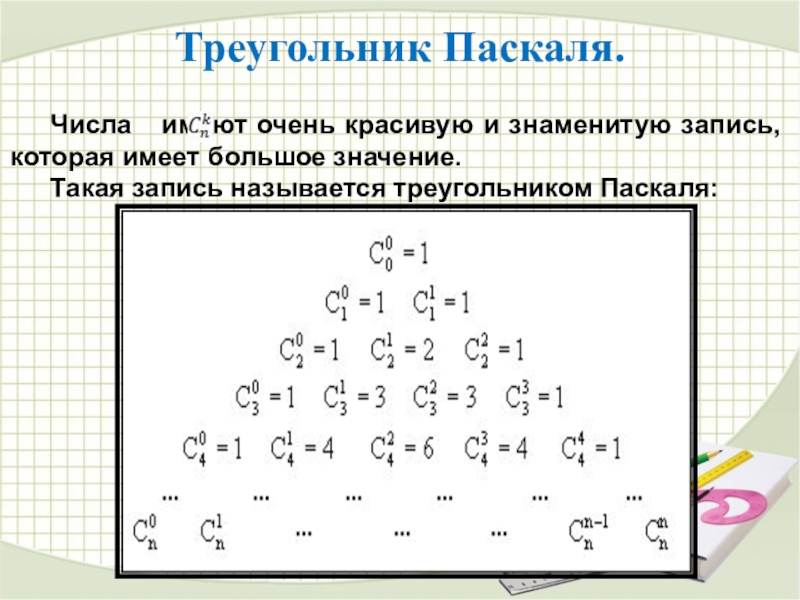
Слайд 26Треугольник Паскаля.
Числа имеют очень красивую и знаменитую запись, которая имеет
Такая запись называется треугольником Паскаля:
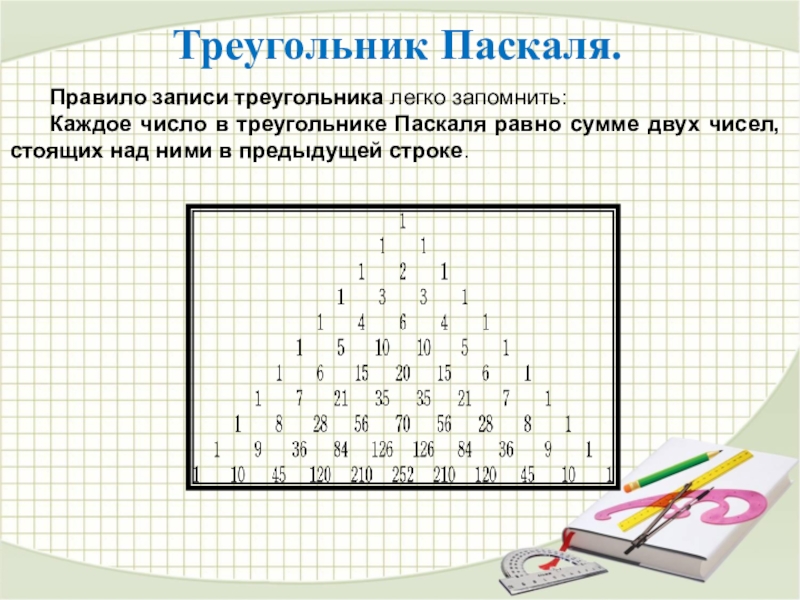
Слайд 27Треугольник Паскаля.
Правило записи треугольника легко запомнить:
Каждое число в треугольнике Паскаля
Слайд 29Бином Ньютона.
Как оказалось, треугольник Паскаля находит свое применение и
Проделаем эту же операцию и для четвертой степени:
Слайд 30Бином Ньютона.
Выпишем для наглядности все наши формулы:
Проведем небольшой анализ
Первое, на что стоит обратить внимание, показатель степени в левой части равен сумме показателей степеней в правой части, для любого слагаемого.
Посмотрите внимательно на коэффициенты в правой части, ни чего не напоминает? Коэффициенты образуют треугольник Паскаля.
Слайд 31 Бином Ньютона
Бином Ньютона – это выражение вида
При возведении
Слайд 34Бином Ньютона.
Пример. Раскрыть скобки: а) б)
Решение. Применим
а)
Вычислим все коэффициенты:
В итоге получаем:
б)
Слайд 36Проверь себя
1. Сколькими способами 4 вора могут разбежаться на 4 разные
2. Из колоды в 36 карт выбирают 5 карт и одновременно открывают их. Найдите число всех возможных вариантов выбранных карт.
3. Сколькими способами из класса, где учатся 24 ученика, можно выбрать: а)двух дежурных; б)старосту и помощника старосты?
Ответ: а)276;
б)552.
4. «Проказница Мартышка, Осёл, Козёл да косолапый Мишка задумали сыграть квартет». Сколькими способами они могут выбрать каждый для себя по одному инструменту из 10 данных различных инструментов?
Ответ:
Слайд 37ЗАДАНИЕ 1. В группе 9 человек. Сколько можно образовать разных подгрупп
ЗАДАНИЕ 2. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую — 5 и в третью — 12. Сколькими способами это можно сделать?
ЗАДАНИЕ 3. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?
Слайд 39РЕШЕНИЕ ЗАДАЧ
№ 1.Вычислите:
№ 2. В классе изучают 9 предметов. Сколькими
№ 3. Сколько существует способов для обозначения вершин данного четырехугольника с помощью букв А,В,С,D,E,F?
№ 4. В классе 30 человек. Сколькими способами могут быть выбраны из их состава староста и казначей?
№ 5. В чемпионате по футболу участвуют 10 команд. Сколько существует различных возможностей занять командам первые три места?
Слайд 40Задача 1. Сколько различных двухзначных чисел
можно записать с помощью цифр
что в каждой записи нет одинаковых цифр?
РАЗМЕЩЕНИЯ БЕЗ ПОВТОРЕНИЙ
12,13,14,
21,23,24
31,32,34,
41,42,43
По правилу произведения 43 = 12
Все соединения отличаются друг от друга
либо составом(12 и 24), либо порядком(12 и 12)
Слайд 41Литература
Алгебра и начала математического анализа 11 класс,
Колягин Ю.М., Ткачев М.В.,
М. : «Просвещение», 2011