- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Задачи на переливание
Содержание
- 1. Презентация по теме Задачи на переливание
- 2. I. ОпределениеЗадачи на переливание – это задачи,
- 3. Метод рассужденийМетод таблицМетод графовМетод математического бильярдаГеометрический способМетод трилинейных координатII. Способы решения
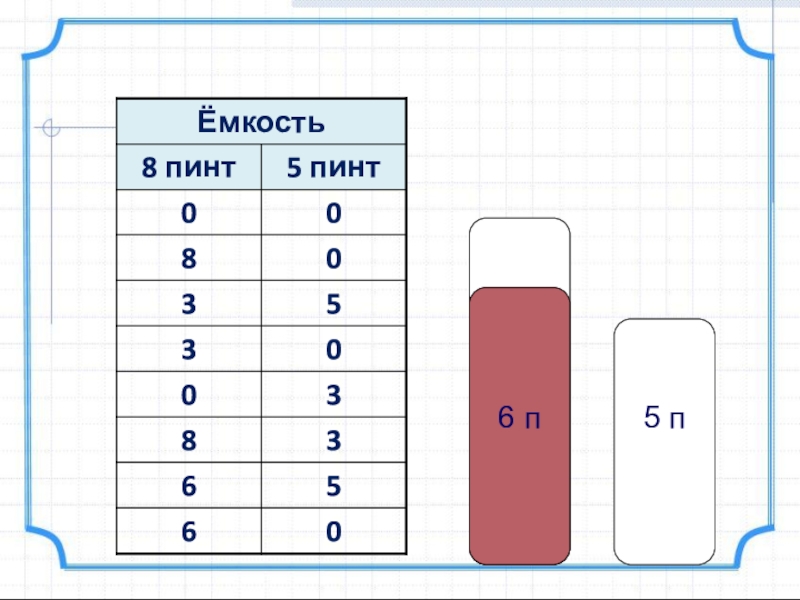
- 4. III. Метод таблиц 5л 3лЗадача №1.Восьмиведерный
- 5. Задача ПуассонаФранцузский математик, механик и физик.Решил эту
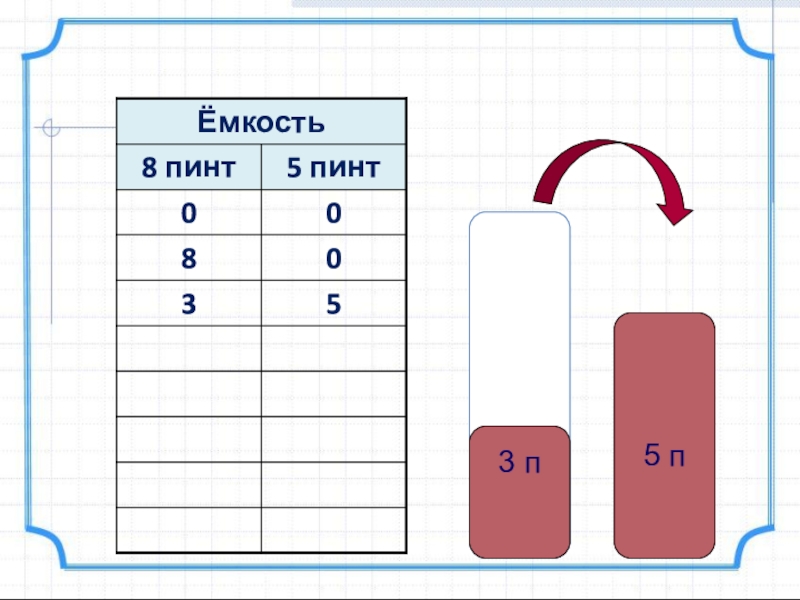
- 6. 8 п 5 п
- 7. 8 п 5 п
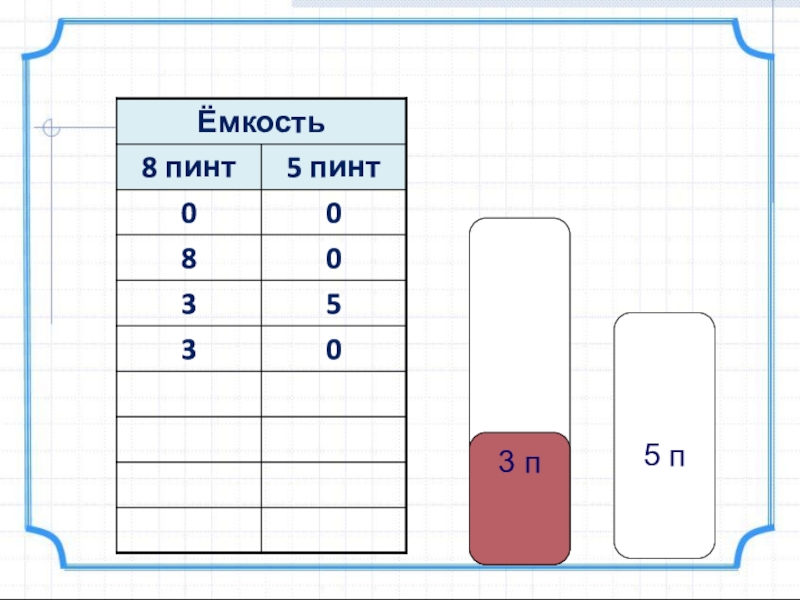
- 8. 5 п 3 п
- 9. 5 п 3 п
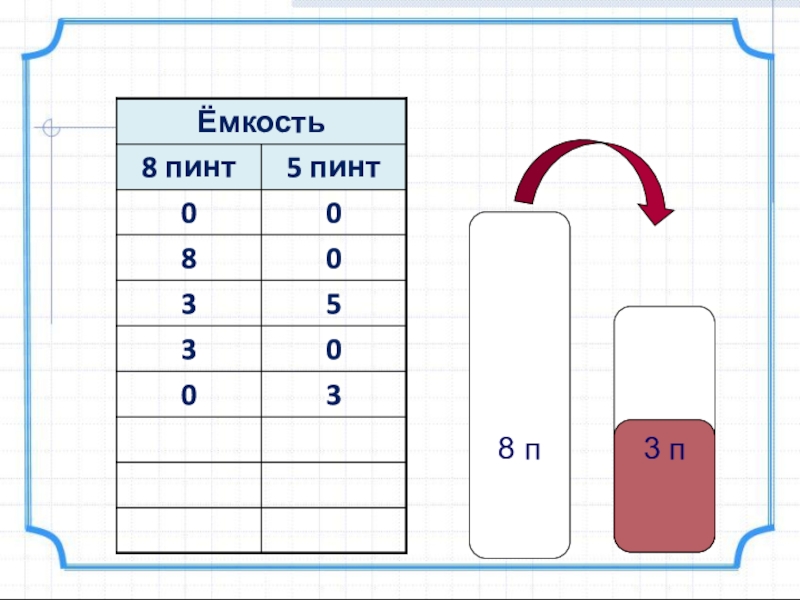
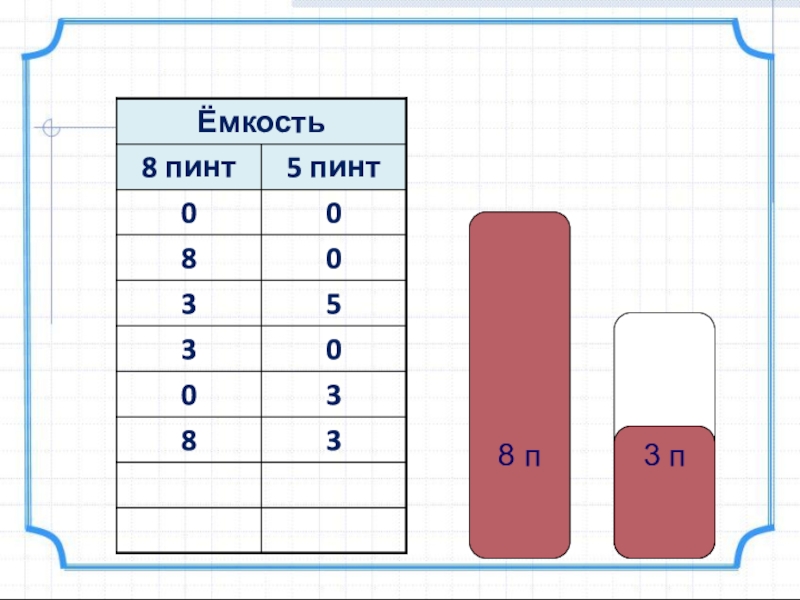
- 10. 8 п 3 п
- 11. 8 п 3 п
- 12. 5 п 6 п
- 13. 5 п 6 п
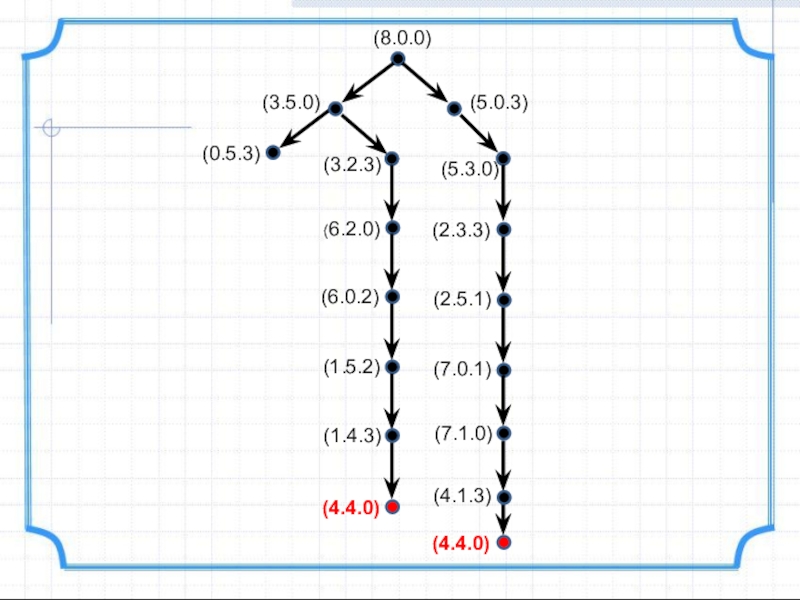
- 14. IV. Метод графовЗадача №1. (2-ой способ решения)Восьмиведерный
- 15. (8.0.0)(3.5.0)(0.5.3)(5.0.3)(3.2.3)(6.2.0)(6.0.2)(1.5.2)(1.4.3)(4.4.0)(5.3.0)(2.3.3)(2.5.1)(7.0.1)(7.1.0)(4.1.3)(4.4.0)
- 16. Построить «бильярдный стол» из равносторонних треугольников, длины
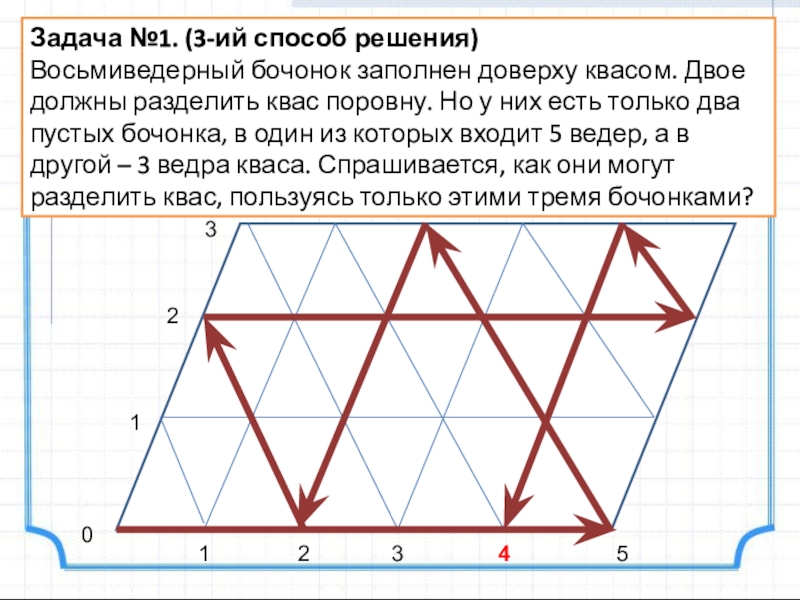
- 17. Задача №1. (3-ий способ решения)Восьмиведерный бочонок заполнен
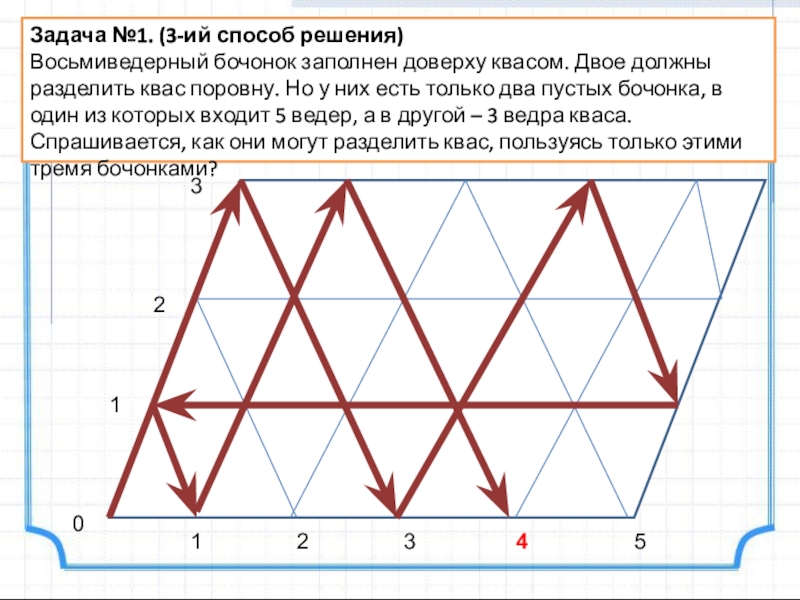
- 18. Задача №1. (3-ий способ решения)Восьмиведерный бочонок заполнен
- 19. Задача №2.Карлсону срочно нужно налить 6
- 20. Задача №2.Карлсону срочно нужно налить 6
- 21. Задача №3. Имеется сосуды вместимостью 12, 9
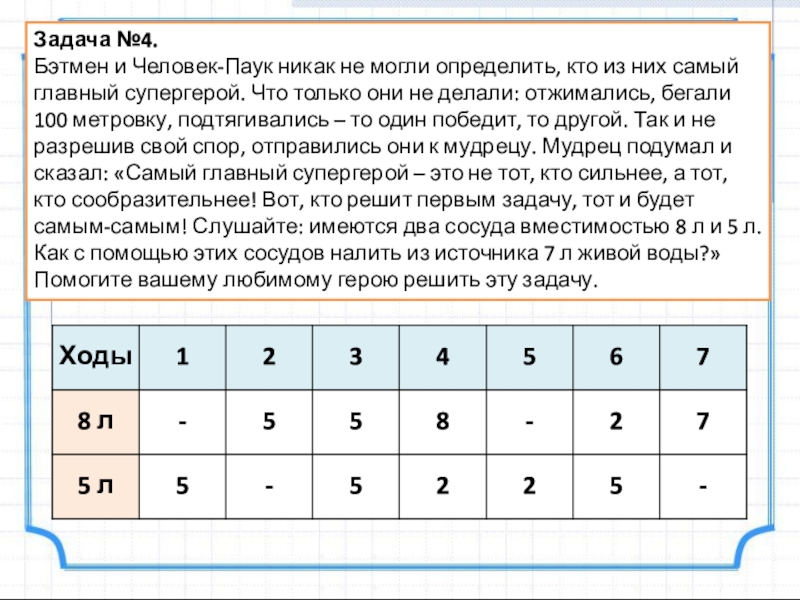
- 22. Задача №4. Бэтмен и Человек-Паук никак не
- 23. Домашнее задание*
Слайд 2I. Определение
Задачи на переливание –
это задачи, в которых с помощью
Особенности:
Все сосуды без делений
Нельзя переливать жидкости "на глаз"
Простейший прием решения состоит в переборе возможных вариантов.
Слайд 3Метод рассуждений
Метод таблиц
Метод графов
Метод математического бильярда
Геометрический способ
Метод трилинейных координат
II. Способы решения
Слайд 4III. Метод таблиц
5л
3л
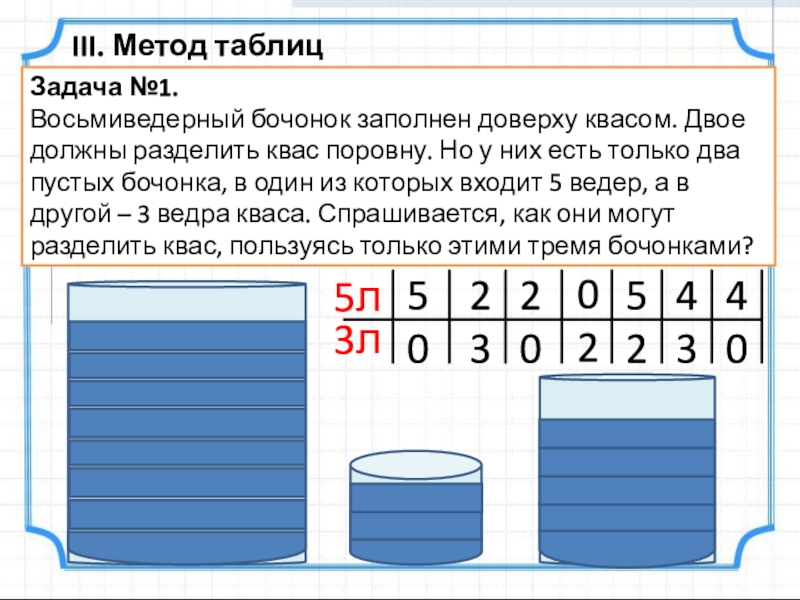
Задача №1.
Восьмиведерный бочонок заполнен доверху квасом. Двое
2
0
0
2
5
2
4
3
4
0
5
0
2
3
Слайд 5Задача Пуассона
Французский математик, механик и физик.
Решил эту задачу в юности и
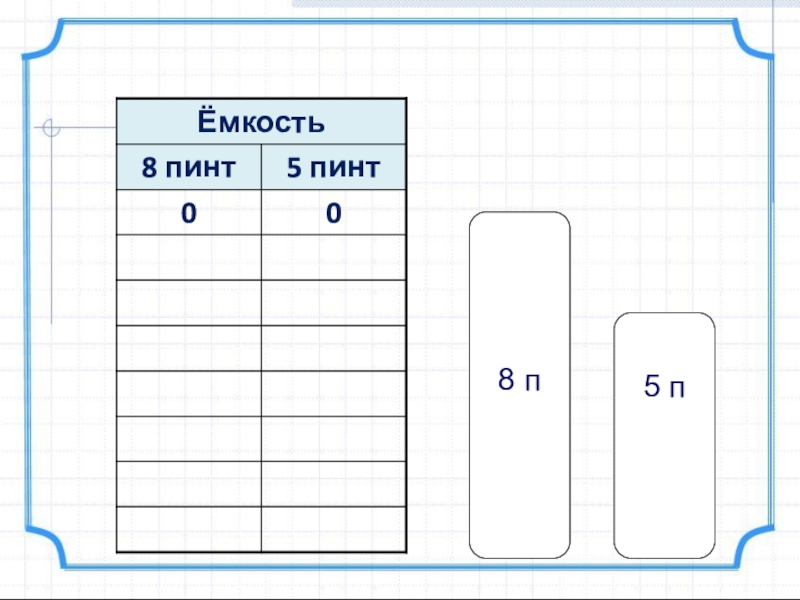
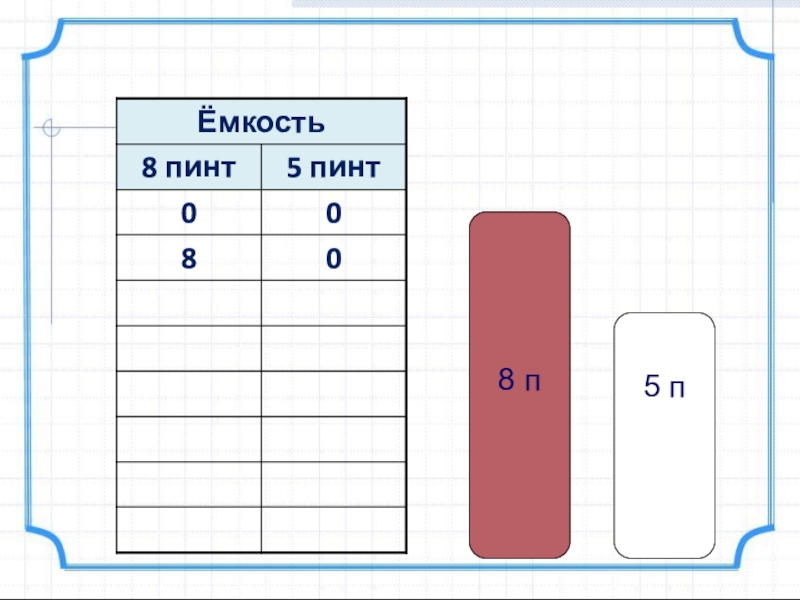
Один человек имеет в бочонке 12 пинт вина (пинта – старинная французская мера объема, 1 пинта ≈ 0,568 л) и хочет подарить половину вина, но у него нет сосуда в 6 пинт, однако имеются два пустых сосуда объемом 8 пинт и 5 пинт. Как с их помощью отлить ровно 6 пинт вина?
Слайд 14IV. Метод графов
Задача №1. (2-ой способ решения)
Восьмиведерный бочонок заполнен доверху квасом.
Присвоим каждому бочонку номер:
Бочонку в 8 ведер - № 1
Бочонку в 5 ведер - № 2
Бочонку в 3 ведра - № 3
Слайд 15
(8.0.0)
(3.5.0)
(0.5.3)
(5.0.3)
(3.2.3)
(6.2.0)
(6.0.2)
(1.5.2)
(1.4.3)
(4.4.0)
(5.3.0)
(2.3.3)
(2.5.1)
(7.0.1)
(7.1.0)
(4.1.3)
(4.4.0)
Слайд 16Построить «бильярдный стол» из равносторонних треугольников, длины двух сторон которого численно
Из острого угла этого стола вдоль одной из сторон нужно «запустить» шарик, который по закону «угол падения равен углу отражения» будет сталкиваться с бортами стола, показывая тем самым последовательность переливаний.
На бортах стола нанесена шкала, цена деления которой соответствует выбранной единице объема.
В результате движения шарик либо ударяется о бортик в нужной точке (тогда задача имеет решение), либо не ударяется (тогда считается, что задача решения не имеет).
Бильярдный шар может перемещаться только вдоль прямых, образующих сетку на параллелограмме.
V. Метод математического бильярда
Слайд 17Задача №1. (3-ий способ решения)
Восьмиведерный бочонок заполнен доверху квасом. Двое должны
1
1
0
2
3
1
2
3
4
5
Слайд 18Задача №1. (3-ий способ решения)
Восьмиведерный бочонок заполнен доверху квасом. Двое должны
0
1
2
3
1
2
3
4
5
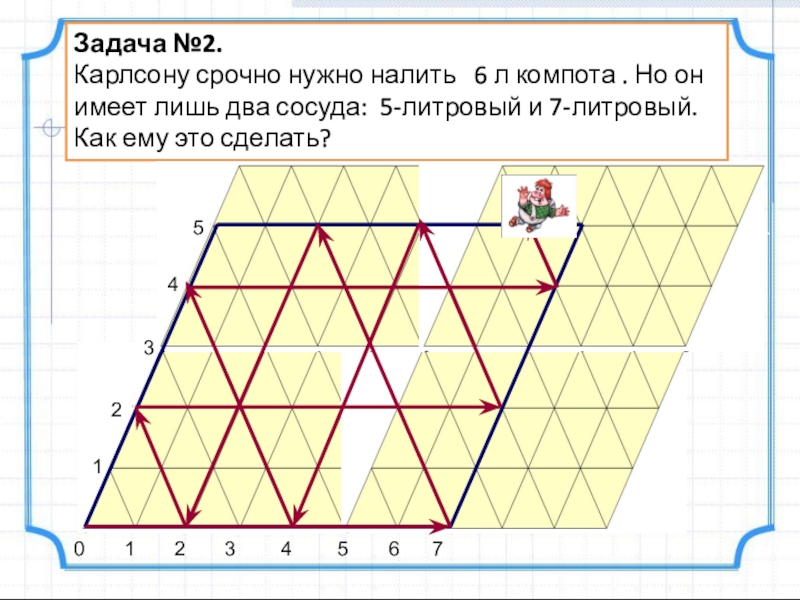
Слайд 19Задача №2.
Карлсону срочно нужно налить 6 л компота . Но
0
1
2
3
4
5
6
7
1
2
3
4
5
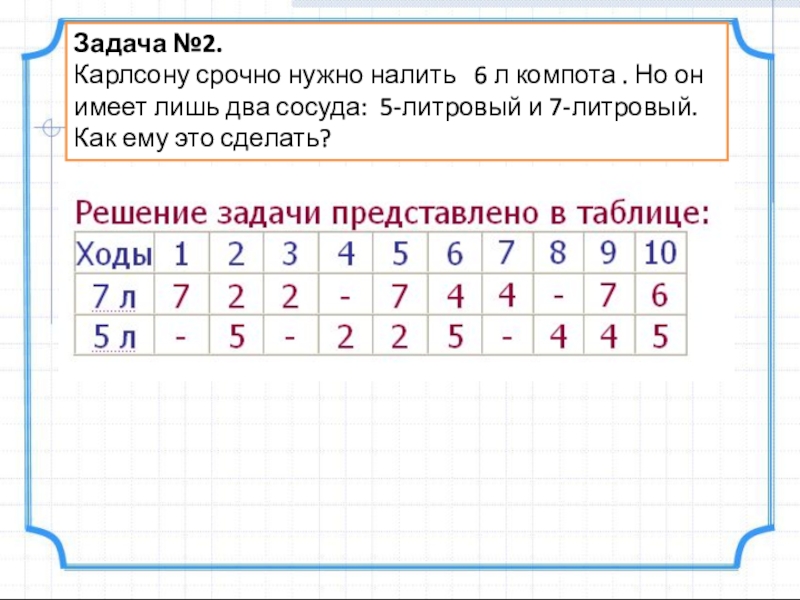
Слайд 20Задача №2.
Карлсону срочно нужно налить 6 л компота . Но
Слайд 21
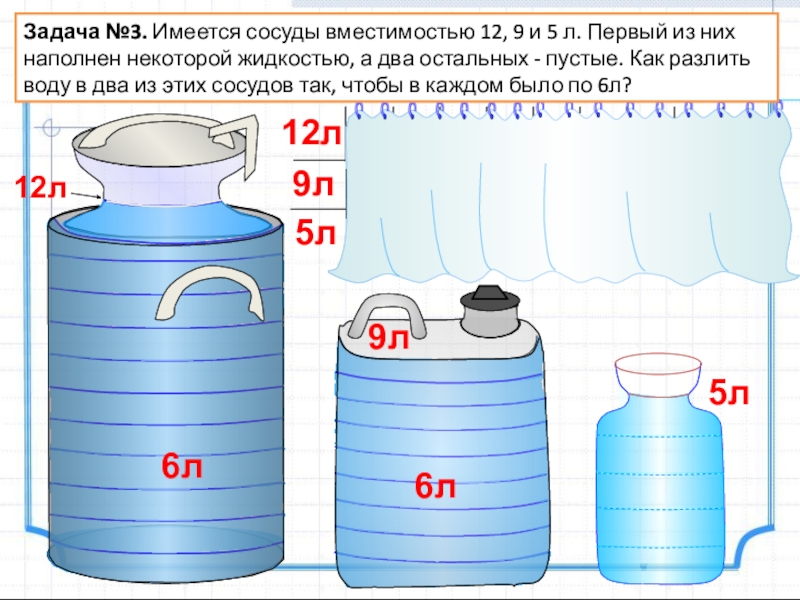
Задача №3. Имеется сосуды вместимостью 12, 9 и 5 л. Первый
12л
9л
5л
6л
6л