- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Вычисление объемов тел с помощью интеграла
Содержание
- 1. Презентация по теме Вычисление объемов тел с помощью интеграла
- 2. Содержание.Алгоритм вычисления объёмов геометрических тел с помощью интеграла. Вычисление объёмов тел.Задача.
- 3. АЛГОРИТМ ВЫЧИСЛЕНИЯ ОБЪЁМОВ ГЕОМЕТРИЧЕСКИХ ТЕЛ С ПОМОЩЬЮ
- 4. Вычисление объёмов тел.1. Заключаем тело Т между
- 5. 6. Разбиваем [a;b] на n – равных
- 6. Задача 1.Найти объём наклонной треугольной призмы с
- 7. Спасибо за внимание
Содержание.Алгоритм вычисления объёмов геометрических тел с помощью интеграла. Вычисление объёмов тел.Задача.
Слайд 2Содержание.
Алгоритм вычисления объёмов геометрических тел с помощью интеграла.
Вычисление объёмов тел.
Задача.
Слайд 3АЛГОРИТМ ВЫЧИСЛЕНИЯ ОБЪЁМОВ ГЕОМЕТРИЧЕСКИХ ТЕЛ С ПОМОЩЬЮ ИНТЕГРАЛА.
1.Ввести
систему координат так, чтобы ось ОХ была перпендикулярна основанию геометрического тела.
2. Найти пределы интегрирования а и b .
3. Провести сечение плоскости перпендикулярно оси ОХ через точку с абсциссой х.
Определить вид сечения, задать формулой его площадь как функцию S(X).
4. Проверить непрерывность функции S(X) на [a;b].
5. V= a∫b S(x)dx
Слайд 4Вычисление объёмов тел.
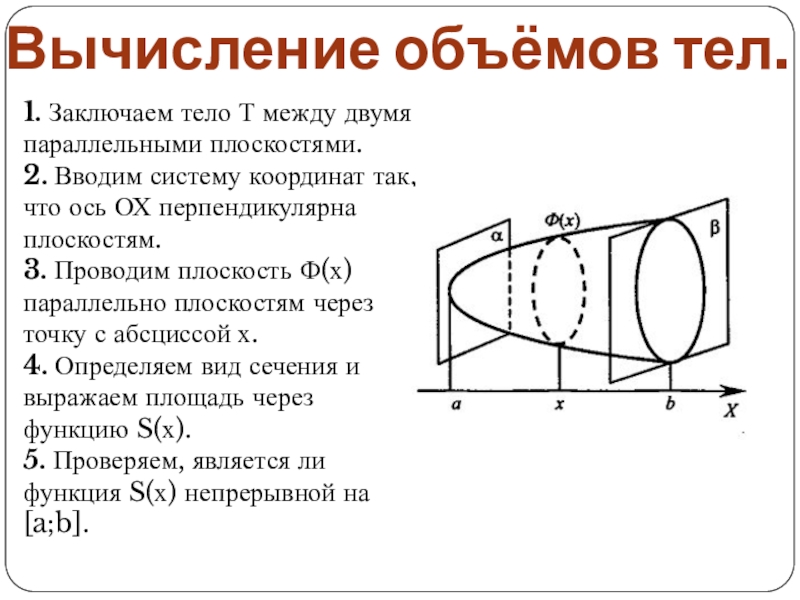
1. Заключаем тело Т между двумя параллельными плоскостями.
2. Вводим
систему координат так, что ось ОХ перпендикулярна плоскостям.
3. Проводим плоскость Ф(х) параллельно плоскостям через точку с абсциссой х.
4. Определяем вид сечения и выражаем площадь через функцию S(х).
5. Проверяем, является ли функция S(х) непрерывной на [a;b].
Слайд 56. Разбиваем [a;b] на n – равных отрезков точками а = х0,
х1, х2, …хn=b
и проводим через Хi плоскости
перпендикулярно ОХ.
7. Плоскости разбивают тело Т на n-
тел Т1, Т2, Т3,... Тn с основаниями
Ф(хi) и высотой Δxi= (b - a)/n
8.V ≈ Vn= (S(x1) + S(x2)+…+ S(xn) ) Δ xi=
=(S(x1) + S(x2) +…+ S(xn))(b - a)/n.
При n ⇒ ∞, Vn ⇒ V.
9.
Слайд 6Задача 1.Найти объём наклонной треугольной призмы с основанием S и высотой
h.
1. Введём ось ОХ перпендикулярно основаниям призмы.
2. (АВС) ∩ OX=a, a=0, (A1B1C1) ∩ OX=b, b=h
3. Проведём плоскость перпендикулярно ОХ через точку с абсциссой х.
А2В2С2-треугольник, равный основаниям.
Площадь А2В2С2 равна S.
4. S(x) непрерывна на [0;h]
Ответ: V=Sh



![Презентация по теме Вычисление объемов тел с помощью интеграла 6. Разбиваем [a;b] на n – равных отрезков точками а = 6. Разбиваем [a;b] на n – равных отрезков точками а = х0, х1, х2, …хn=b и проводим](/img/thumbs/8e7c2d333e80db25eef1ace68c6749ca-800x.jpg)







