- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Вписанные и описанные многоугольники. Правильные многоугольники
Содержание
- 1. Презентация по теме Вписанные и описанные многоугольники. Правильные многоугольники
- 2. Вписанным в окружность называется многоугольник, вершины которого
- 3. Радиус r вписанного круга выражается через стороны
- 4. В четырёхугольник можно вписать окружность, если суммы
- 5. Правильный многоугольник – это многоугольник с равными
- 6. Внутри правильного многоугольника существует точка O ,
- 7. Соотношения сторон и радиусов правильных многоугольников:
- 8. П р и м е р .
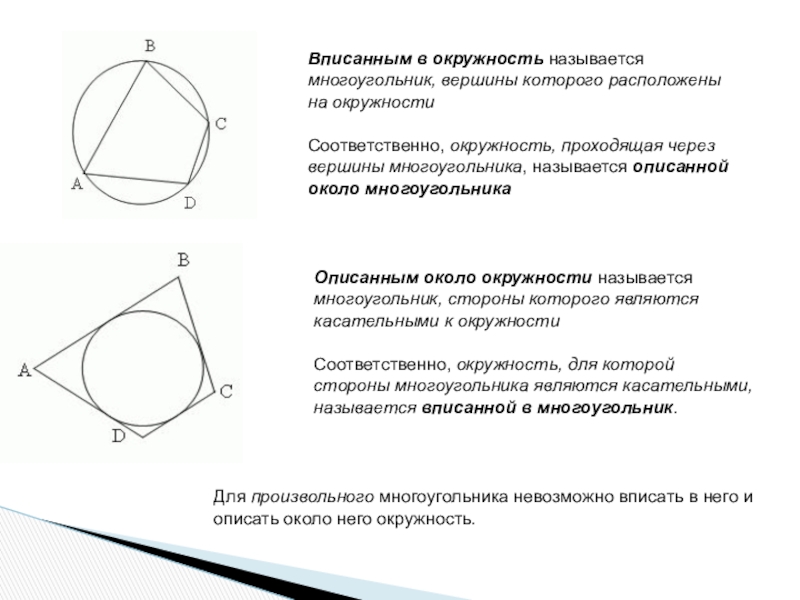
Слайд 2Вписанным в окружность называется многоугольник, вершины которого расположены на окружности
Соответственно,
Описанным около окружности называется многоугольник, стороны которого являются касательными к окружности
Соответственно, окружность, для которой стороны многоугольника являются касательными, называется вписанной в многоугольник.
Для произвольного многоугольника невозможно вписать в него и описать около него окружность.
Слайд 3Радиус r вписанного круга выражается через стороны a, b, c треугольника:
, p = (a+b+c)/2
Радиус R описанного круга выражается формулой:
R =
В любой треугольник возможно вписать окружность и описать около него окружность.
Слайд 4 В четырёхугольник можно вписать окружность, если суммы его противоположных сторон равны.
Центр вписанного круга расположен в точке пересечения диагоналей.
Около четырёхугольника можно описать круг, если сумма его противоположных углов равна 180º.
Для параллелограммов это возможно только для прямоугольника ( квадрата ).
Центр описанного круга лежит в точке пересечения диагоналей.
Вокруг трапеции можно описать круг, если только она равнобокая.
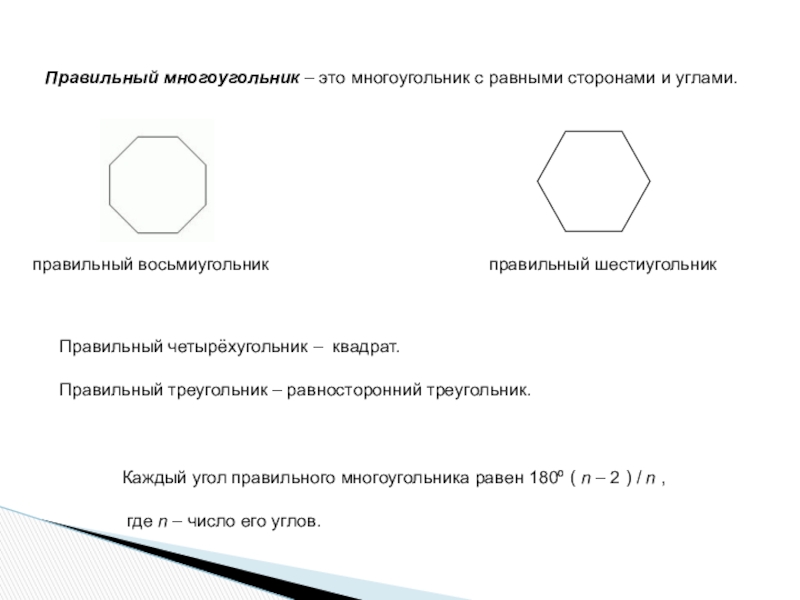
Слайд 5Правильный многоугольник – это многоугольник с равными сторонами и углами.
правильный
правильный шестиугольник
Правильный четырёхугольник – квадрат.
Правильный треугольник – равносторонний треугольник.
Каждый угол правильного многоугольника равен 180º ( n – 2 ) / n ,
где n – число его углов.
Слайд 6 Внутри правильного многоугольника существует точка O , равноудалённая от всех его
Центр правильного многоугольника также равноудалён от всех его сторон ( OP = OQ = OR = … ).
Отрезки OP, OQ, OR, … называются апофемами;
отрезки OA, OB, OC, …– радиусы правильного многоугольника.
В правильный многоугольник можно вписать окружность и около него можно описать окружность.
Центры вписанной и описанной окружностей совпадают с центром правильного многоугольника.
Радиус описанного круга - это радиус правильного многоугольника,
радиус вписанного круга - его апофема.
Слайд 8П р и м е р . Можно ли вырезать квадрат
диаметром 40 см?
Р е ш е н и е . Наибольший квадрат, заключённый в круг, есть вписанный
квадрат. В соответствии с вышеприведенной формулой его
сторона равна:
20 ≈ 28 с≈ 20 · 1,41 см
Следовательно, квадрат со стороной 30 см невозможно вырезать
из круга диаметром 40 см.