- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Треугольник Паскаля
Содержание
- 1. Презентация по теме Треугольник Паскаля
- 2. Историческая справкаПервое упоминание треугольника Паскаля встречается в комментарии
- 3. Паскаль умер, когда ему было 39 лет,
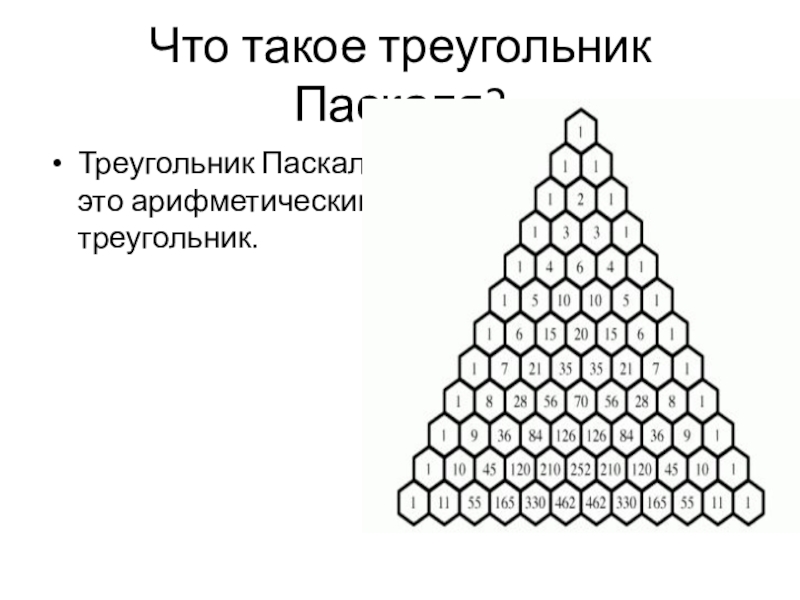
- 4. Что такое треугольник Паскаля?Треугольник Паскаля это арифметический треугольник.
- 5. “Треугольник Паскаля так прост, что выписать его
- 6. Принцип построения треугольника ПаскаляКаждое число равно сумме 2-х чисел, стоящих над ним.
- 7. Гипотеза исследованияТреугольник Паскаля обладает рядом замечательных свойств, поэтому и носит имя одного из выдающихся людей.
- 8. ЦЕЛЬ ИССЛЕДОВАНИЯПривести достаточное количество примеров свойств
- 9. АКТУАЛЬНОСТЬ: Навыки решения задач с применением треугольника
- 10. ОБЪЕКТ ИССЛЕДОВАНИЯ: Числа треугольника ПаскаляПРАКТИЧЕСКАЯ ЗНАЧИМОСТЬ ИССЛЕДОВАНИЯ:В подборе задач, которые можно использовать в учебе.
- 11. Сравним треугольник Паскаля с треугольником у которогопо
- 12. Свойство № 1 Треугольник Паскаля бесконечен
- 13. Свойство № 2 Сумма чисел
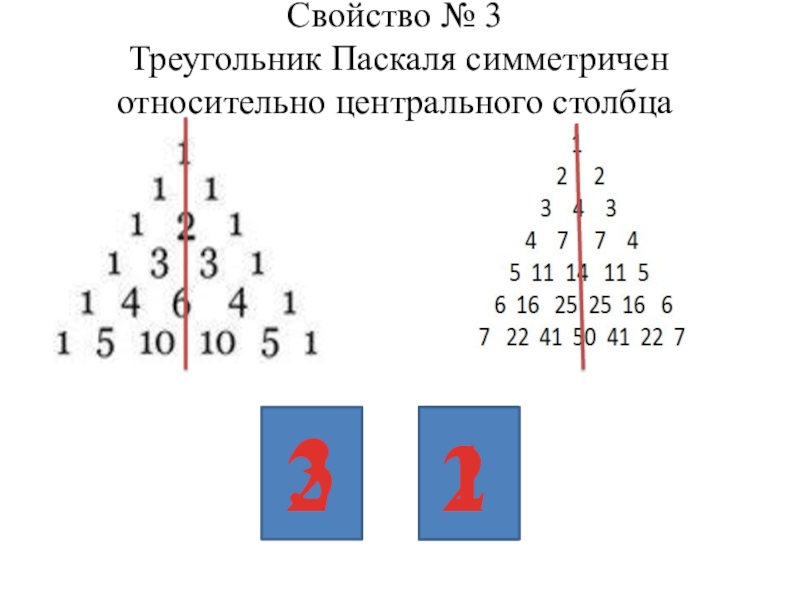
- 14. Свойство № 3 Треугольник Паскаля
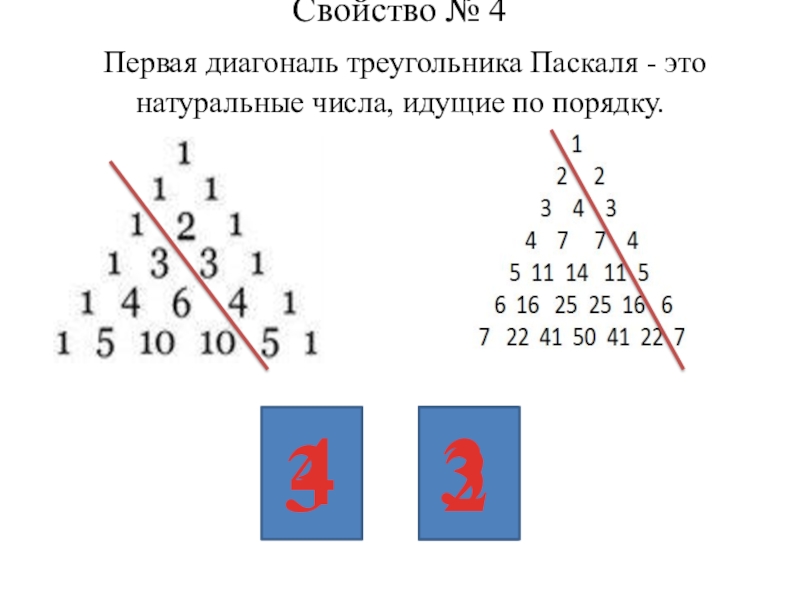
- 15. Свойство № 4 Первая
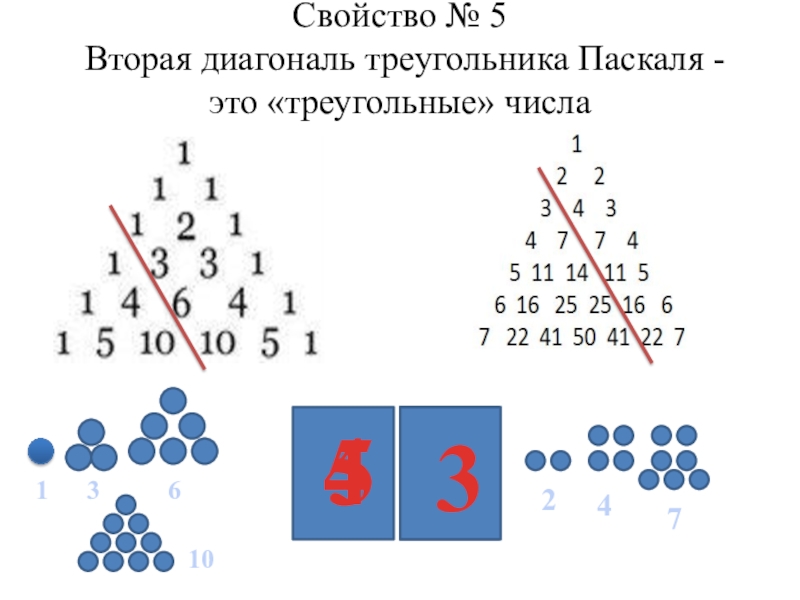
- 16. Свойство № 5 Вторая диагональ
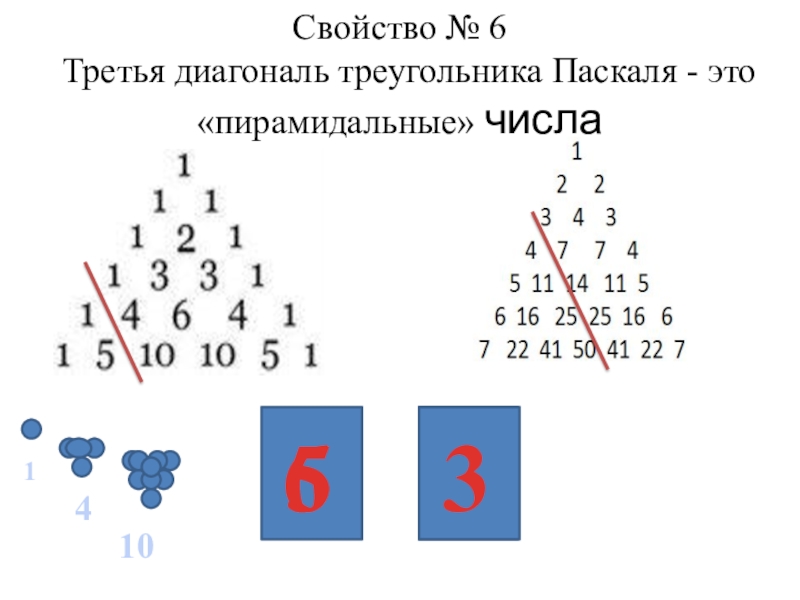
- 17. Свойство № 6 Третья диагональ треугольника
- 18. Свойство № 7 Четвёртая диагональ
- 19. Свойство № 8 Каждое
- 20. Свойство № 9 Каждое число
- 21. Свойство № 10
- 22. Свойство № 11
- 23. Свойство № 12 Если нечётное число
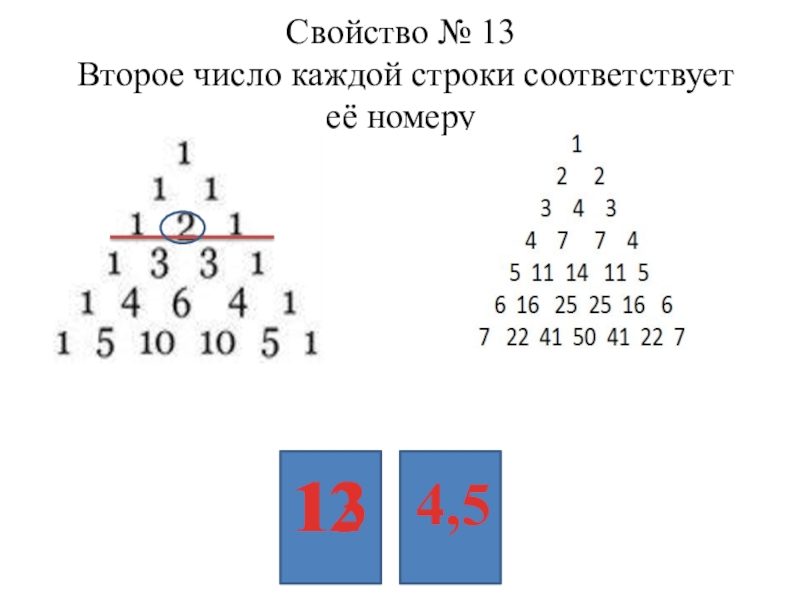
- 24. Свойство № 13 Второе число каждой
- 25. Применение свойств треугольника Паскаля в решении математических
- 26. Задача № 1( олимпиадная) В город А
- 27. Задача № 2 ( комбинаторная)Сколькими способами можно
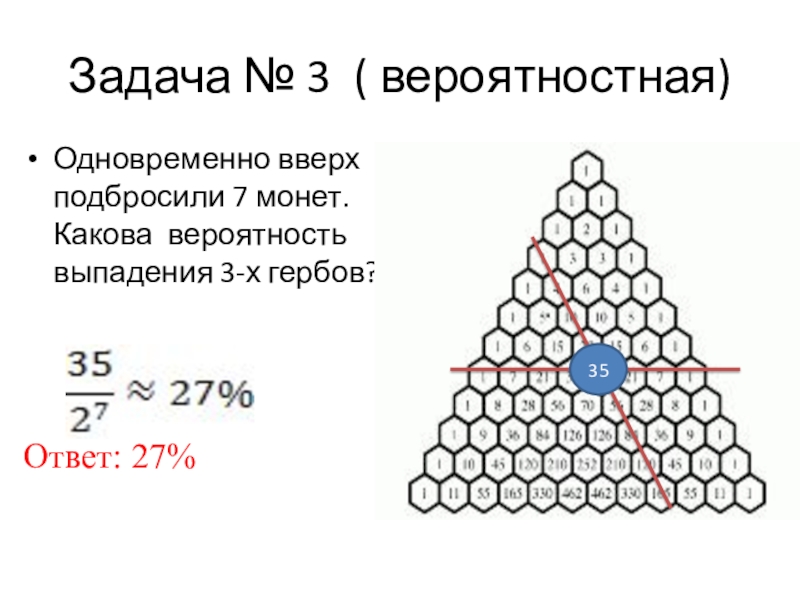
- 28. Задача № 3 ( вероятностная)Одновременно вверх подбросили 7 монет. Какова вероятность выпадения 3-х гербов?Ответ: 27%35
- 29. Задача № 4( алгебраическая) Представить в виде многочлена выражение (а+в)4(а+в)0=1(а+в)1=1а+1в(а+в)2=1а2+2ав+1в2……………………………….(а+в)4=1а4+4а3в+6а2в2+4ав3+1в4
- 30. ВыводВ ходе моего исследования я убедились, что
- 31. Литература и интернет источники:Энциклопедия для детей. Т.11.
- 32. Спасибо за внимание!
Слайд 1Треугольник Паскаля
Автор:
ученица 7 класса
Лапина Наталья
Научный руководитель
Учитель математики
Никитченко Вера Евгеньевна
Слайд 2Историческая справка
Первое упоминание треугольника Паскаля встречается в комментарии индийского математика X века Халаюдхи к трудам
Слайд 3Паскаль умер, когда ему было 39 лет, но, несмотря на столь
Слайд 5“Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок.
Мартин Гарднер
Слайд 7Гипотеза исследования
Треугольник Паскаля обладает рядом замечательных свойств, поэтому и носит имя
Слайд 8 ЦЕЛЬ ИССЛЕДОВАНИЯ
Привести достаточное количество примеров свойств чисел треугольника Паскаля и
ЗАДАЧИ ИССЛЕДОВАНИЯ
Найти и изучить имеющийся материал о треугольнике Паскаля
Выявить свойства чисел треугольника Паскаля.
Определить применение свойств чисел треугольника Паскаля.
Провести эксперимент по сравнению свойств различных арифметических треугольников
Сформулировать вывод и итоги исследования.
Слайд 9АКТУАЛЬНОСТЬ: Навыки решения задач с применением треугольника Паскаля помогут в рамках
МЕТОДЫ ИССЛЕДОВАНИЯ:: анализ научно-популярной литературы; систематизация; сравнение; эксперимент.
Слайд 10ОБЪЕКТ ИССЛЕДОВАНИЯ: Числа треугольника Паскаля
ПРАКТИЧЕСКАЯ ЗНАЧИМОСТЬ ИССЛЕДОВАНИЯ:
В подборе задач, которые можно
Слайд 11Сравним треугольник Паскаля с треугольником у которого
по боковым сторонам- ряд натуральных
1
2 2
3 4 3
4 7 7 4
5 11 14 11 5
6 16 25 25 16 6
7 22 41 50 41 22 7
Слайд 13 Свойство № 2 Сумма чисел в строках треугольника Паскаля - 2n,
1
1
1=2°
1+1=2¹
1+2+1=4=2²
1+3+3+1=8=2³
1+4+6+4+1=16= 24
1
2+2=4=2²
3+4+3=10
4+7+7+4=22
5+11+14+11+5=46
2
Слайд 15 Свойство № 4 Первая диагональ треугольника Паскаля - это натуральные числа,
3
2
4
3
Слайд 18
Свойство № 7
Четвёртая диагональ треугольника Паскаля это уже фигурные числа в
6
3
7
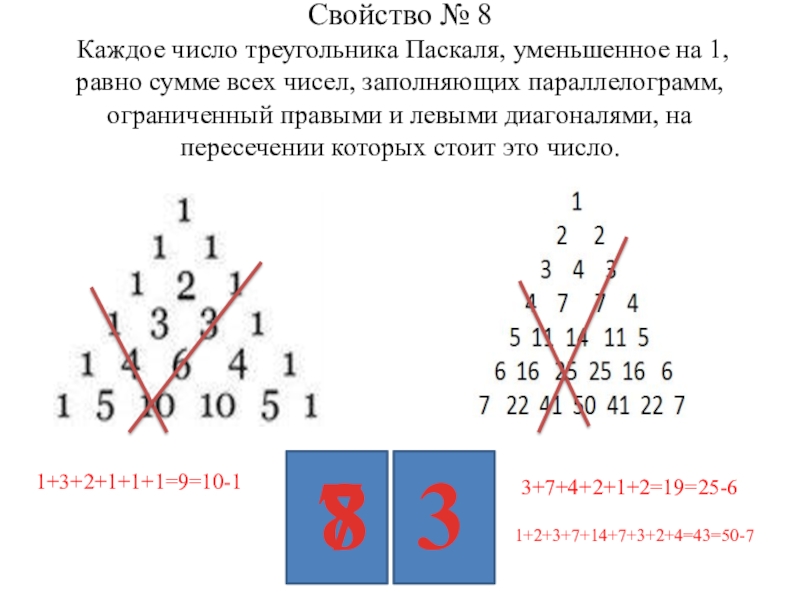
Слайд 19 Свойство № 8 Каждое число треугольника Паскаля, уменьшенное на 1, равно
7
3
1+3+2+1+1+1=9=10-1
3+7+4+2+1+2=19=25-6
1+2+3+7+14+7+3+2+4=43=50-7
8
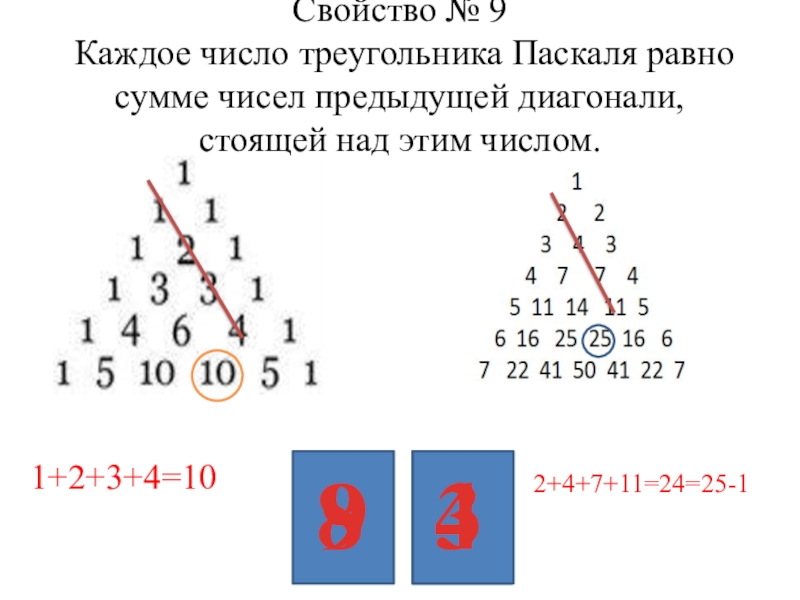
Слайд 20 Свойство № 9 Каждое число треугольника Паскаля равно сумме чисел предыдущей
8
3
1+2+3+4=10
2+4+7+11=24=25-1
9
4
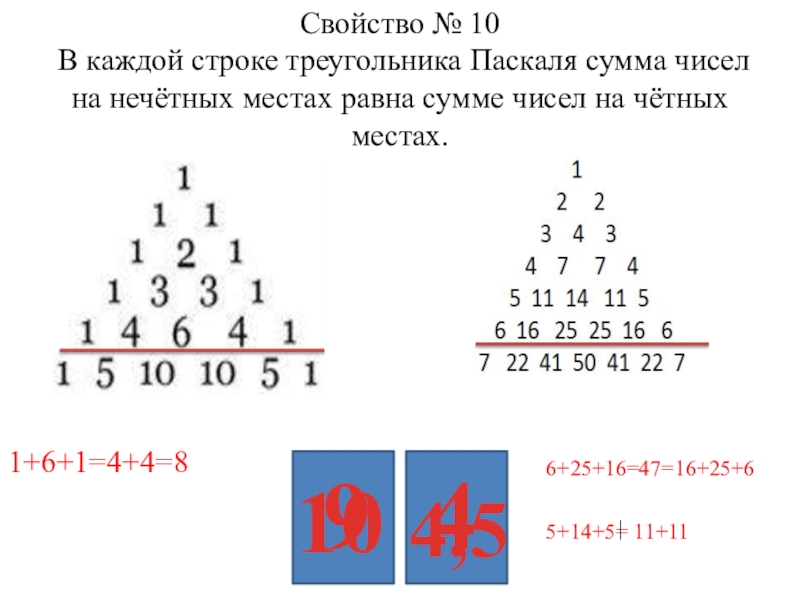
Слайд 21 Свойство № 10 В каждой строке треугольника Паскаля сумма чисел на
9
4
1+6+1=4+4=8
6+25+16=47=16+25+6
5+14+5= 11+11
10
4,5
Слайд 22 Свойство № 11 Если номер строки треугольника Паскаля – простое число,
10
4,5
N=5
5,10,10,5- делятся на 5
N=5
11,14,11- не делятся на 5
11
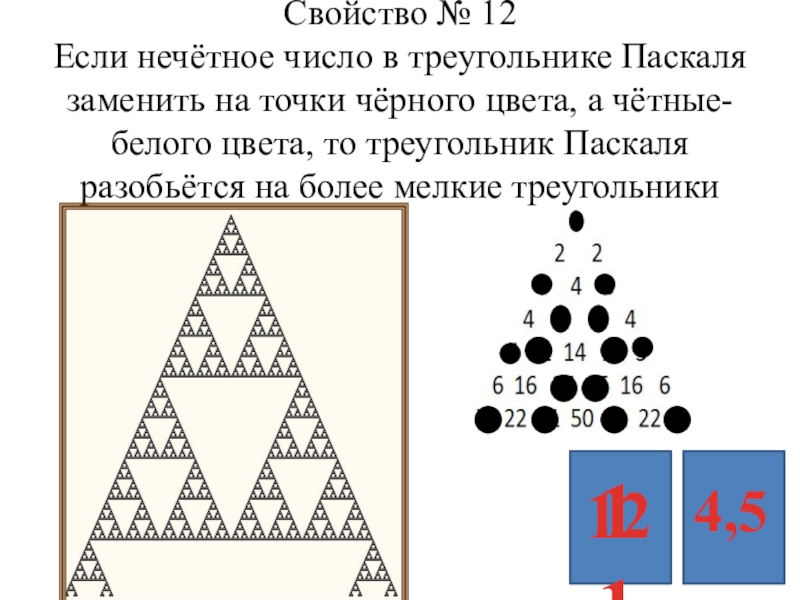
Слайд 23 Свойство № 12 Если нечётное число в треугольнике Паскаля заменить на точки
11
4,5
12
Слайд 25Применение свойств треугольника Паскаля в решении математических задач.
Свойства треугольника Паскаля, наверное,
Слайд 26Задача № 1( олимпиадная)
В город А можно попасть по единственному
Ответ:1,10,45,120,
210,252,210,120,45,
10,1ч.
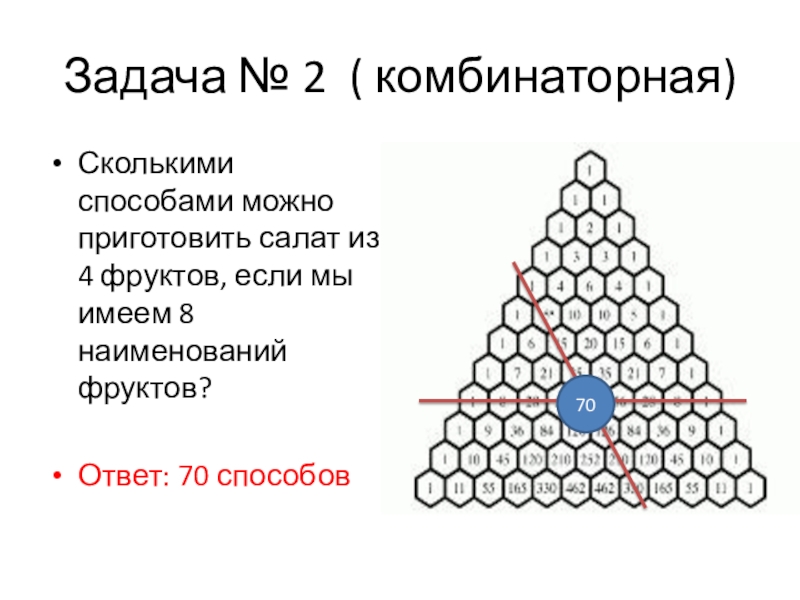
Слайд 27Задача № 2 ( комбинаторная)
Сколькими способами можно приготовить салат из 4
Ответ: 70 способов
70
Слайд 28Задача № 3 ( вероятностная)
Одновременно вверх подбросили 7 монет. Какова вероятность
Ответ: 27%
35
Слайд 29Задача № 4( алгебраическая)
Представить в виде многочлена выражение (а+в)4
(а+в)0=1
(а+в)1=1а+1в
(а+в)2=1а2+2ав+1в2
……………………………….
(а+в)4=1а4+4а3в+6а2в2+4ав3+1в4
Слайд 30Вывод
В ходе моего исследования я убедились, что треугольник Паскаля, несмотря на
Слайд 31Литература и интернет источники:
Энциклопедия для детей. Т.11. Математика/ Сост. Аксенова М.Д.
Энциклопедический словарь юного математика / Сост. Савин А.П. – Педагогика, 1989.
http://www.pereplet.ru/nauka/Soros/pdf/0005_101.pdf
http://www.arbuz.uz/u_treug.html
http://ru.wikipedia.org/wiki/Треугольник_Паскаля
http://biostudlife.hiblogger.net
http://mech.math.msu.su/~shvetz/54/inf/perl-problems/chPascalTriangle.xhtml
http://image.websib.ru/07/text_article.htm?342
http://www.slideboom.com.