научно-практическая конференция
«Первые шаги в науку»
Исследовательская работа на тему:
«Системы счисления. От древности до современности»
Выполнил:
Ученик 4 «Б» класса
Артюхов Станислав
Научный руководитель:
Торосян Маргарита Саркисовна
Сочи
2019
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Системы счисления -история и современность
Содержание
- 1. Презентация по теме Системы счисления -история и современность
- 2. Первобытные системы счетаПервобытные люди знали только понятия
- 3. Единичная системаВ древности записи чисел делались в
- 4. Счет на пальцах десяткамиОчень широко был распространен
- 5. Счет на пальцах по двенадцать Некоторые народы пересчитывали
- 6. Система счислений Древнего Египта Древние египтяне использовали только
- 7. Она является
- 8. Вавилонская система счисленияДля малых чисел вавилонская система
- 9. Алфавитные системы счисленияВ древности использовались системы, в
- 10. История «арабских» чиселЦифры – это специальные знаки,
- 11. Позиционные системы счисленияРассмотренные нами иероглифические и алфавитные
- 12. Самые распространенные позиционные системы счисления это двоичная,
- 13. Заключительная частьЗавершая свое исследование, я провел практическую
- 14. Слайд 14
Первобытные системы счетаПервобытные люди знали только понятия «один», «два» и «много». Позже люди научились считать и придумали знаки, означающие определенное количество предметов., Эти знаки у разных народов были разные, но принцип записи чисел у большинства древних
Слайд 1Министерство образования Российской Федерации
Государственное бюджетное общеобразовательное учреждение
Средняя общеобразовательная школа № 87
Сочи
Городская
Слайд 2Первобытные системы счета
Первобытные люди знали только понятия «один», «два» и «много».
Позже люди научились считать и придумали знаки, означающие определенное количество предметов., Эти знаки у разных народов были разные, но принцип записи чисел у большинства древних народов был схожим-непозиционным. То есть каждый знак или символ в записи чисел обозначал определенное число и значение этого числа не зависело от места этого символа в записи.
Слайд 3Единичная система
В древности записи чисел делались в виде зарубок на палке,
узлов на веревке, выложенных в ряд камешков. Такая система записи чисел называется единичной (или унарной) так как любое число в ней формируется путем повтрения одного и того же знака нужное количество раз.
Единичная система была очень громоздкой и неудобной и люди стали искать более компактные способы счета. Единичные системы счисления встречаются и сегодня, но очень редко. Например, этой системой пользуются малыши, когда показывают на пальцах свой возраст. Единичная система является фундаментом арифметики и до сих пор вводит детей в мир счета.
Единичная система была очень громоздкой и неудобной и люди стали искать более компактные способы счета. Единичные системы счисления встречаются и сегодня, но очень редко. Например, этой системой пользуются малыши, когда показывают на пальцах свой возраст. Единичная система является фундаментом арифметики и до сих пор вводит детей в мир счета.
Слайд 4Счет на пальцах десятками
Очень широко был распространен счет на пальцах, и
названия некоторых чисел берут свое начало от этого способа подсчета. Как пример, во многих языках число пять соответствует названию руки или пяти пальцев (у славян пядь – это рука). И, так как в качестве вычислительного инструмента у человека были пальцы, поэтому и счет чаще всего вели группами по 5 или по 10 предметов. Отсюди и пошли пятеричная и десятеричная системы счисления.
Слайд 5Счет на пальцах по двенадцать
Некоторые народы пересчитывали большим пальцем руки фаланги
на остальных четырех пальцах, при этом учитывали, что каждый палец состоит из трех фаланг, таким образом, люди имели в распоряжении двенадцать объектов счета. Вот так и родилась севременная двенадцатиричная система. Люди и до сих пор делят на 12 часы в сутках , месяцы в году. Круг содержит тридцать дюжин градусов, фут делится на двенадцать дюймов. Дюжинами считают многие предметы.
Слайд 6Система счислений Древнего Египта
Древние египтяне использовали только десятичную систему счисления. Единицу
обозначали одной вертикальной чертой. Для чисел до 10 рисовали соответсвующее число черточек. Для означения числа 10 египтяне ввели новый символ, похожий на подкову, для 100 - рисунок лотоса и так далее до миллиона. С течением времени эти знаки приобрели более простой вид. Записывались цифры числа начиная с больших значений и заканчивая наименьшими. Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду.
Слайд 7 Она является примером непозиционной системы, которая
сохранилась до наших дней. В основе римской системы счисления лежат знаки.
Если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае меньшая цифра не может повторяться), то меньшая вычитается из большей». Например: VII=5+1+1=7; IX=10-1=9
Римская система нумерации десятичная, но непозиционная.
Если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае меньшая цифра не может повторяться), то меньшая вычитается из большей». Например: VII=5+1+1=7; IX=10-1=9
Римская система нумерации десятичная, но непозиционная.
Слайд 8Вавилонская система счисления
Для малых чисел вавилонская система счисления была такой же,
как Египетская. Но для чисел начиная с 60 вавилоняне ввели революционный принцип позиционности - то есть зависимости значения символа от его местоположения в записи числа. Запись числа разбивалась на позиции» и знаки более высокого порядка располагались слева.
Вавилонская система знаков, кратных 60 представляла собой огромное значение для математики. Деление часа на 60 минут, а одной минуты – на 60 секунд идет от вавилонской системы счисления
Вавилонская система знаков, кратных 60 представляла собой огромное значение для математики. Деление часа на 60 минут, а одной минуты – на 60 секунд идет от вавилонской системы счисления
Слайд 9Алфавитные системы счисления
В древности использовались системы, в которых числа изображались буквами
алфавита. Например, греческая алфавитная нумерация-числа от 1 до 9 обозначали первыми девятью буквами греческого алфавита: ά (Альфа) = 1, β (Бета) = 2, γ (Гамма) = 3 и т.д.. Для обозначения десятков применялись следующие девять букв, для сотен последние 9 букв. У русских роль цифр играли не все буквы славянского алфавита, а только те из них, которые имелись в греческом алфавите. Над буквой, обозначавшей цифру, ставился специальный значок ~ («титло»). Числовые значения букв возрастали в том же порядке, в каком следовали буквы в греческом алфавите (порядок букв славянского алфавита был несколько иным)
Слайд 10История «арабских» чисел
Цифры – это специальные знаки, с помощью которых записывают
числа.
Арабы использовали десятичную систему счисления. Они взяли лучшее из знаний накопленных в Греции, Китае и Индии, упростили запись цифр, и около 2 тысяч лет назад они приобрели вид
получив название «арабские числа». В XII веке нашей эры арабские цифры распространились по всей Европе, потому что такая запись чисел была удобнее и проще. Слово «цифра» перешло к нам от арабов по наследству, нуль или «пусто» называли «сифра». Сейчас цифрами называются любые знаки для записи чисел.
Арабы использовали десятичную систему счисления. Они взяли лучшее из знаний накопленных в Греции, Китае и Индии, упростили запись цифр, и около 2 тысяч лет назад они приобрели вид
получив название «арабские числа». В XII веке нашей эры арабские цифры распространились по всей Европе, потому что такая запись чисел была удобнее и проще. Слово «цифра» перешло к нам от арабов по наследству, нуль или «пусто» называли «сифра». Сейчас цифрами называются любые знаки для записи чисел.
Слайд 11Позиционные системы счисления
Рассмотренные нами иероглифические и алфавитные системы счисления имели существенный
недостаток – в них было очень трудно выполнять арифметические операции. Этого неудобства нет у позиционных систем.
Система счисления называется позиционной, если количественные значения символов, используемых для записи чисел, зависят от их положения (места, позиции) в коде числа.
ПРИМЕР. Рассмотрим запись числа 3333 в десятичной системе
3333 = 3*1000 + 3*100 + 3*10 + 3*1
Здесь 10 – это основание системы счисления. Каждая цифра 3 в этой записи умножается на вес этой позиции. То есть можно сказать, что число 3333 состоит из 3-х единиц, 3-х десяток, 3-х сотен и 3-х тысяч.
Система счисления называется позиционной, если количественные значения символов, используемых для записи чисел, зависят от их положения (места, позиции) в коде числа.
ПРИМЕР. Рассмотрим запись числа 3333 в десятичной системе
3333 = 3*1000 + 3*100 + 3*10 + 3*1
Здесь 10 – это основание системы счисления. Каждая цифра 3 в этой записи умножается на вес этой позиции. То есть можно сказать, что число 3333 состоит из 3-х единиц, 3-х десяток, 3-х сотен и 3-х тысяч.
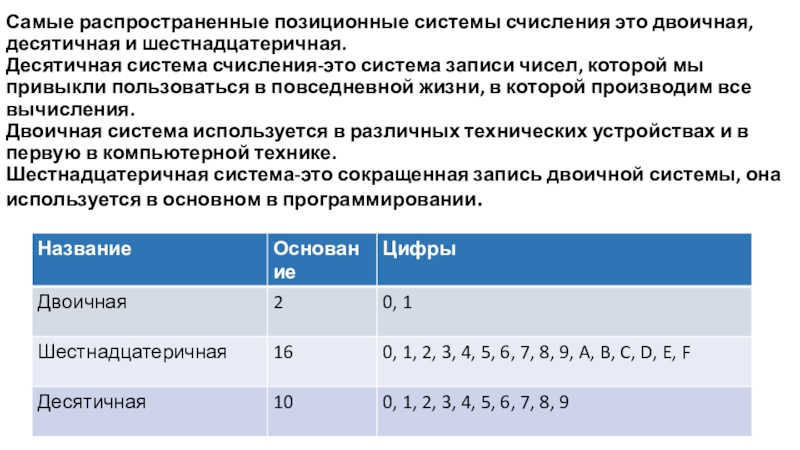
Слайд 12Самые распространенные позиционные системы счисления это двоичная, десятичная и шестнадцатеричная. Десятичная система
счисления-это система записи чисел, которой мы привыкли пользоваться в повседневной жизни, в которой производим все вычисления.
Двоичная система используется в различных технических устройствах и в первую в компьютерной технике.
Шестнадцатеричная система-это сокращенная запись двоичной системы, она используется в основном в программировании.
Слайд 13Заключительная часть
Завершая свое исследование, я провел практическую работу, попробовав при помощи
компьютерной программы перевести числа одной системы счисления в другие. Для этого я использовал исходный код программы преобразования символов на языке С и с его помощью преобразовал число 2020, дату текущего года.
Результаты расчетов