умнее»
В. Шукшин
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Применение производной
Содержание
- 1. Презентация по теме Применение производной
- 2. 13.02.17 Возрастание и убывание функции. Точки экстремума функции.
- 3. Функция y=f(x) называется возрастающей в некотором интервале,
- 4. Если производная функции >0 на некотором интервале,
- 5. Находим область определения функции f(x).Вычисляем производную f’(x)
- 6. Точку x=x0 называют точкой минимума функции y=f(x),
- 7. Если функция y=f(x) имеет экстремум в точке
- 8. Если производная f’(x) при переходе через точку
- 9. Учебник Колмогоров, п. 22-23, №283(в,г); №292(б,г).Выучить условия монотонности и существования экстремумов функции.Задание на дом:
13.02.17 Возрастание и убывание функции. Точки экстремума функции.
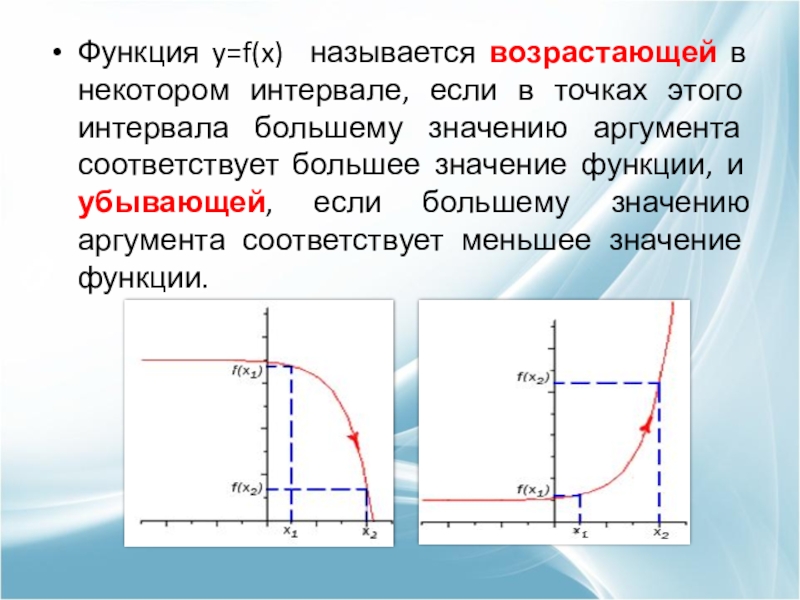
Слайд 3Функция y=f(x) называется возрастающей в некотором интервале, если в точках этого
интервала большему значению аргумента соответствует большее значение функции, и убывающей, если большему значению аргумента соответствует меньшее значение функции.
Слайд 4Если производная функции >0 на некотором интервале, то функция в этом
интервале монотонно возрастает.
Если производная функции <0 на некотором интервале, то функция в этом интервале монотонно убывает.
Если производная функции <0 на некотором интервале, то функция в этом интервале монотонно убывает.
Слайд 5Находим область определения функции f(x).
Вычисляем производную f’(x) данной функции.
Находим точки, в
которых f’(x)=0 или не существует. Эти точки называются критическими для функции f(x).
Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности.
Исследуем знак f’(x) на каждом интервале. Если f’(x)›0, то на этом интервале f(x) возрастает; если f’(x)‹0, то на таком интервале функция f(x) убывает.
Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности.
Исследуем знак f’(x) на каждом интервале. Если f’(x)›0, то на этом интервале f(x) возрастает; если f’(x)‹0, то на таком интервале функция f(x) убывает.
Правило нахождения интервалов
монотонности
Слайд 6Точку x=x0 называют точкой минимума функции y=f(x), если у этой точки
существует окрестность, для всех точек которой выполняется неравенство f(x)≥f(x0).
Точку x=x0 называют точкой максимума функции y=f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x)≤f(x0).
Точку x=x0 называют точкой максимума функции y=f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x)≤f(x0).
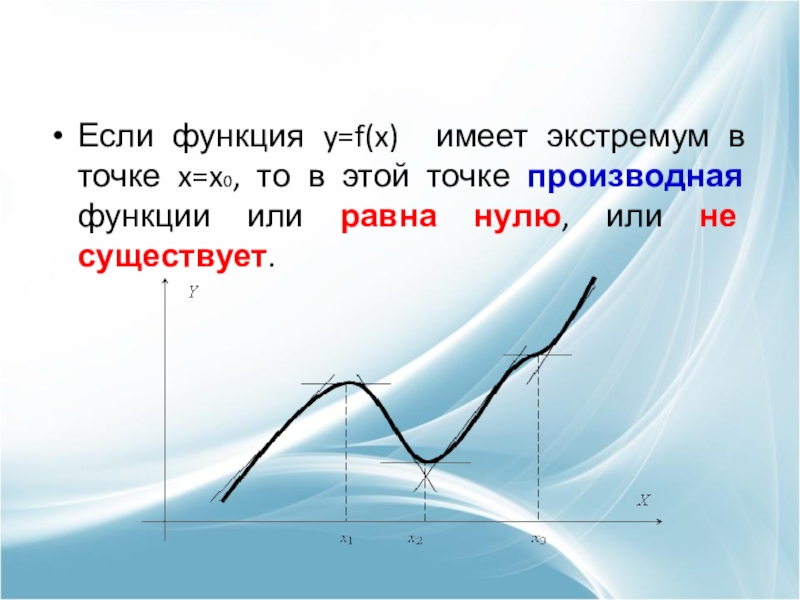
Слайд 7Если функция y=f(x) имеет экстремум в точке x=x0, то в этой
точке производная функции или равна нулю, или не существует.
Слайд 8Если производная f’(x) при переходе через точку x0 меняет знак, то
точка x0 является точкой экстремума функции f(x).
Если производная меняет знак с + на –, то точка будет являться точкой максимума, если с – на +, то точка будет точкой минимума
Если производная меняет знак с + на –, то точка будет являться точкой максимума, если с – на +, то точка будет точкой минимума
Слайд 9Учебник Колмогоров, п. 22-23, №283(в,г); №292(б,г).
Выучить условия монотонности и существования экстремумов
функции.
Задание на дом: