- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Первый признак равенства треугольников
Содержание
- 1. Презентация по теме Первый признак равенства треугольников
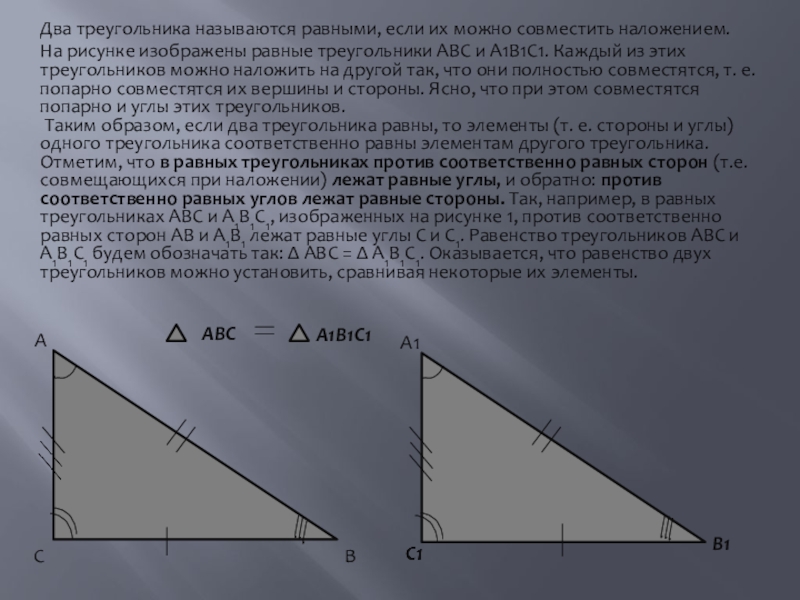
- 2. Два треугольника называются равными, если их можно
- 3. Первый признак равенства треугольников. Если две стороны и
- 4. АА1ВВ1С1Теорема 2Второй признак равенства треугольников. Если сторона и
- 5. Пример 1Дано: ∆АВС ∆DEF∠ А = ∠
- 6. Пример 2Отрезки АВ и CD пересекаются в
- 7. Пример 3Дано: ∆ABC и ∆DEF АВ =
- 8. Пример 4На рисунке углы DAB и СВА,
- 9. Слайд 9
Слайд 1Равенства треугольника
Работу выполнила:
Ученица 8б класса
Бухарцева Дарья Алексеевна
А
В
С
В1
С1
А1
Слайд 2Два треугольника называются равными, если их можно совместить наложением.
На рисунке изображены
A1
С
В
A
В1
АВС
А1В1С1
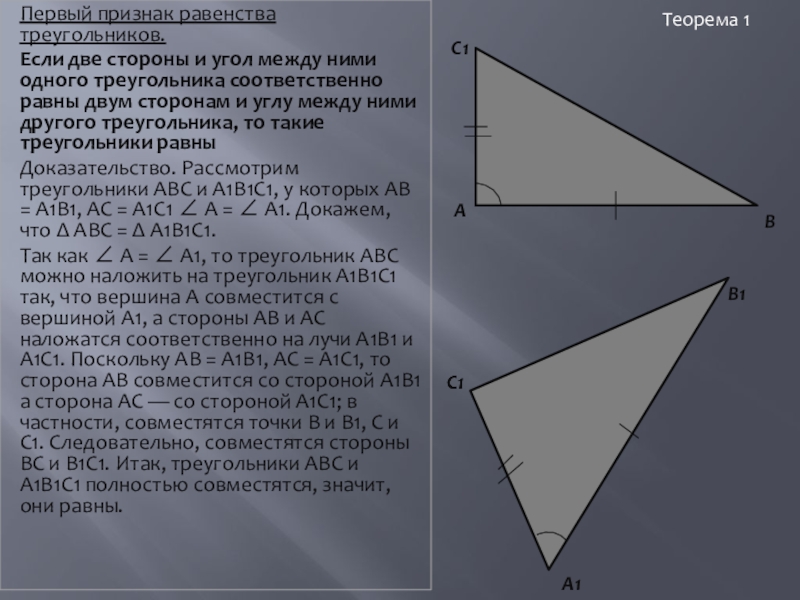
Слайд 3Первый признак равенства треугольников.
Если две стороны и угол между ними одного
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1. Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
А
А1
В
В1
С1
Теорема 1
Слайд 4А
А1
В
В1
С1
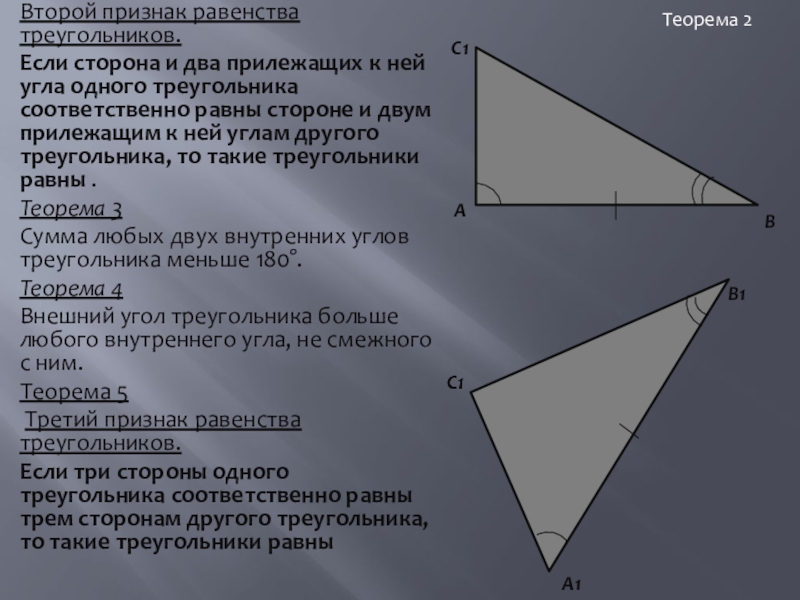
Теорема 2
Второй признак равенства треугольников.
Если сторона и два прилежащих к ней
Теорема 3
Сумма любых двух внутренних углов треугольника меньше 180°.
Теорема 4
Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Теорема 5
Третий признак равенства треугольников.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Слайд 5Пример 1
Дано: ∆АВС ∆DEF
∠ А = ∠ Е
АВ = 20
АС = 18 см
DE = 18 см
EF = 20 см.
Док-ть : ∆АВС=∆DEF
Какой угол в треугольнике DEF равен углу В?
Решение:
Данные треугольники равны по первому признаку.
Угол F треугольника DEF равен углу В треугольника ABC, так как эти углы лежат против соответственно равных сторон DE и АС.
А
В
С
D
E
F
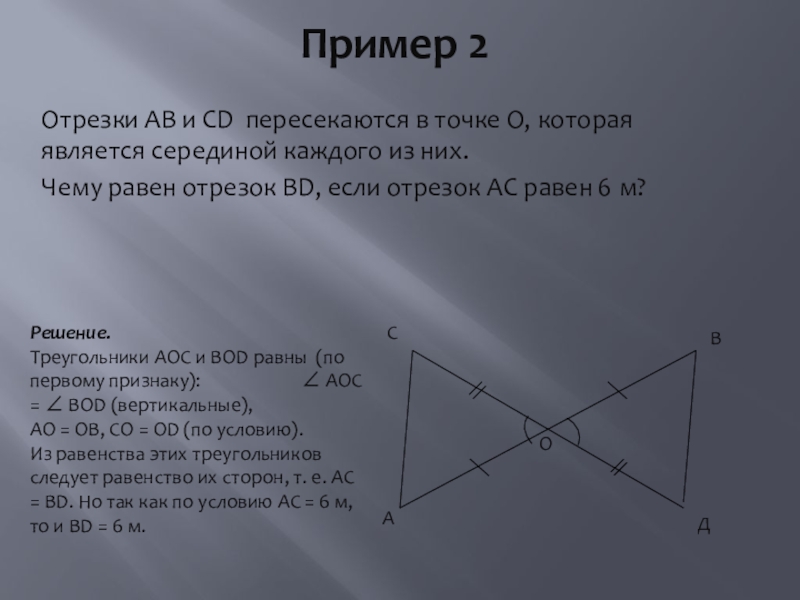
Слайд 6Пример 2
Отрезки АВ и CD пересекаются в точке О, которая является
Чему равен отрезок BD, если отрезок АС равен 6 м?
А
С
В
Д
О
Решение.
Треугольники АОС и BOD равны (по первому признаку): ∠ АОС = ∠ BOD (вертикальные),
АО = ОВ, СО = OD (по условию).
Из равенства этих треугольников следует равенство их сторон, т. е. АС = BD. Но так как по условию АС = 6 м, то и BD = 6 м.
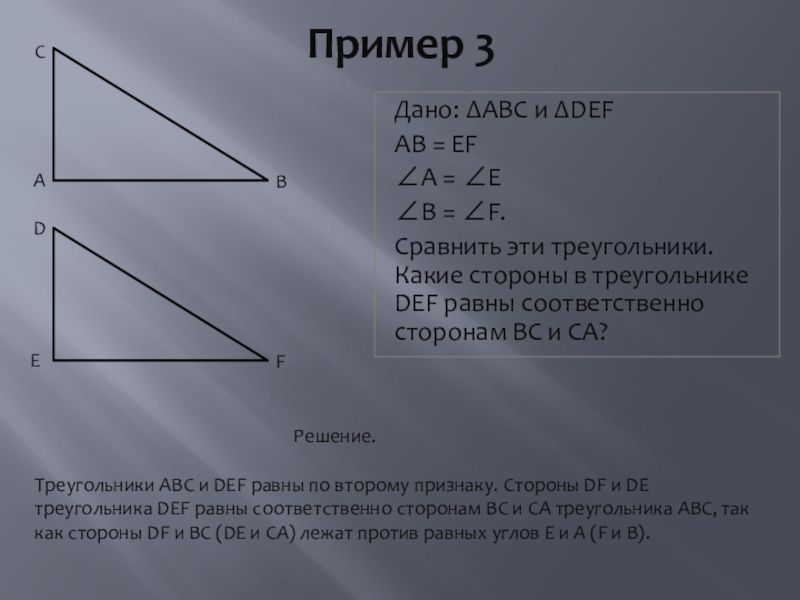
Слайд 7Пример 3
Дано: ∆ABC и ∆DEF
АВ = EF
∠A = ∠E
∠B =
Сравнить эти треугольники. Какие стороны в треугольнике DEF равны соответственно сторонам ВС и СА?
Решение.
Треугольники ABC и DEF равны по второму признаку. Стороны DF и DE треугольника DEF равны соответственно сторонам ВС и СА треугольника ABC, так как стороны DF и ВС (DE и СА) лежат против равных углов Е и A (F и В).
С
А
В
D
E
F
Слайд 8Пример 4
На рисунке углы DAB и СВА, CAB и DBA равны,
СА = 13 м. Найти DB.
Решение.
Треугольники АСВ и ADB имеют одну общую сторону АВ и по два равных угла, которые прилежат к этой стороне. Следовательно, треугольники АСВ и ADB равны (по второму признаку). Из равенства этих треугольников следует равенство сторон BD и АС, т. е. BD = 13 м.