- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Параллельность прямых и плоскостей
Содержание
- 1. Презентация по теме Параллельность прямых и плоскостей
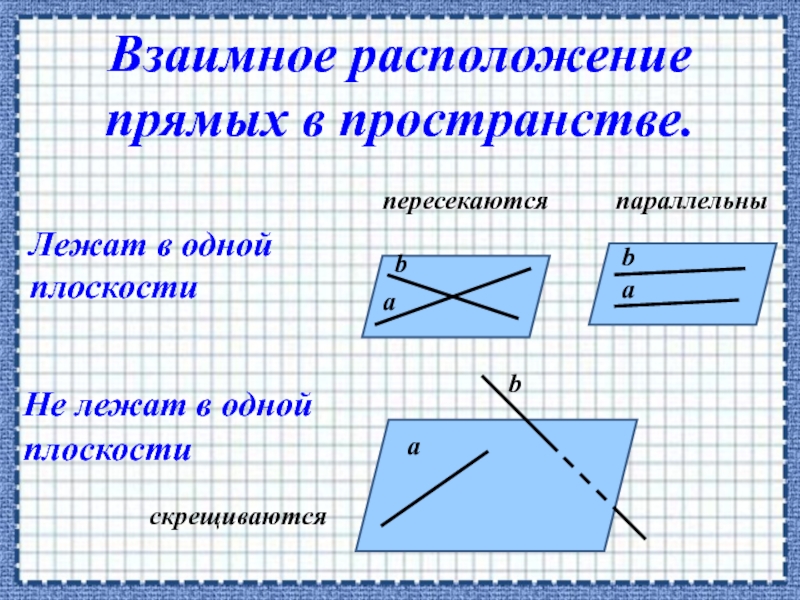
- 2. пересекаютсяпараллельныаааbbbскрещиваютсяЛежат в одной плоскостиНе лежат в одной плоскостиВзаимное расположение прямых в пространстве.
- 3. Параллельными называются прямые,лежащие в однойплоскости и неимеющие точекпересечения.
- 4. Теорема о параллельных прямых.Через любую точку пространства,
- 5. …они лежат на параллельных прямыхОтрезки в пространстве
- 6. Лемма о параллельных прямыхЕсли одна из параллельных
- 7. Доказательство:асв1вβ α В1 случай. а, в,
- 8. Теорема о параллельных прямых.КabДано: К aДоказать:
- 9. Задание 1 Вставьте пропущенные слова Единственную
- 10. Задание 2 Определите: верно, ли утверждение? НетНетДаДаНет
- 11. Задание 2 Определите: верно, ли утверждение? НетНетНетДа
- 12. Задание 3 Дано: ВС=АС, СС1 АА1,АА1=22
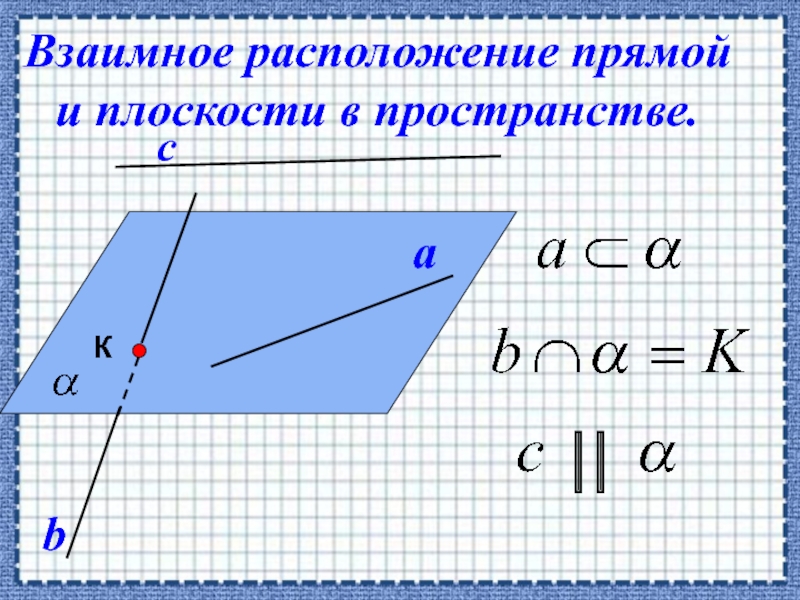
- 13. Взаимное расположение прямой и плоскости в пространстве.
- 14. Если прямая, не лежащая в данной плоскости,параллельна
- 15. 1.Через прямые a и b проведем плоскость
- 16. Дано: а αа β; β
- 17. AВСПлоскость проходит через сторону АС АВС.
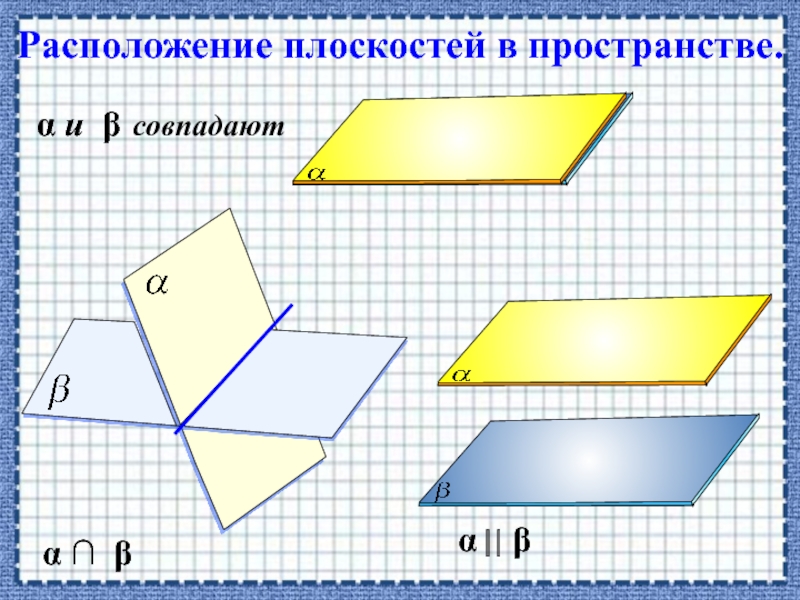
- 18. Расположение плоскостей в пространстве.α β α и β совпадаютα β
- 19. Признак параллельности двух плоскостей.Если две пересекающиеся прямые
- 20. ТеоремаЧерез точку вне данной плоскости можно провести
- 21. β•АαДокажем единственность плоскости β методом от противного.•С•Ввсβ1
- 22. Если две параллельные плоскости пересечены третьей, то
- 23. Отрезки параллельных прямых, заключенные между параллельными
- 24. 1. если плоскости не пересекаются, то они
- 25. Через данную точку А провести плоскость,
- 26. Задача 2. Доказать, что через каждую из
- 27. Спасибо за внимание!
Слайд 2пересекаются
параллельны
а
а
а
b
b
b
скрещиваются
Лежат в одной плоскости
Не лежат в одной плоскости
Взаимное расположение прямых в
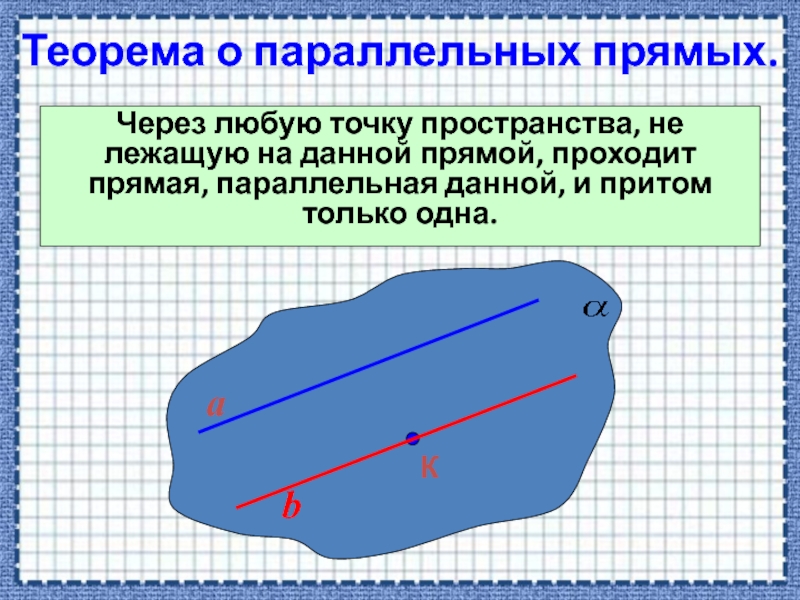
Слайд 4Теорема о параллельных прямых.
Через любую точку пространства, не лежащую на данной
К
a
b
Слайд 5…они лежат на параллельных прямых
Отрезки в пространстве называются параллельными, если …
Лучи
Параллельные отрезки,
параллельные лучи
в пространстве.
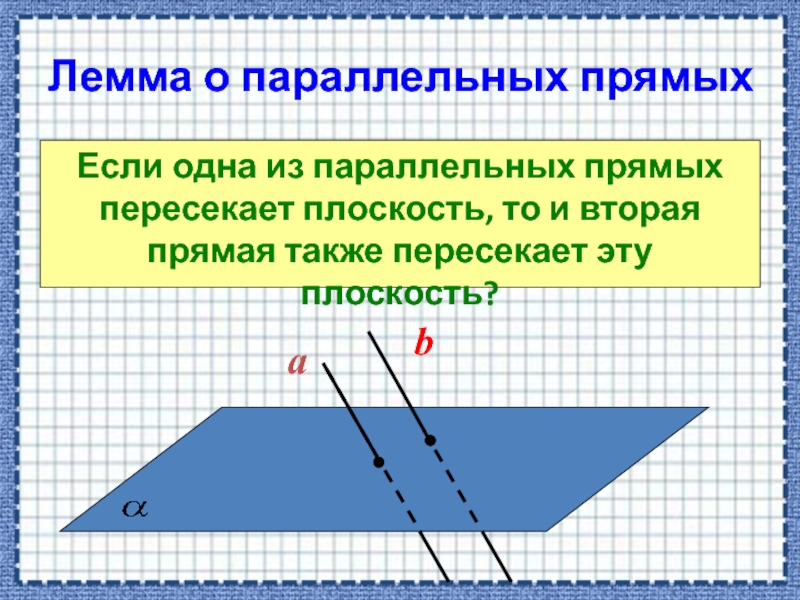
Слайд 6Лемма о параллельных прямых
Если одна из параллельных прямых пересекает плоскость, то
a
b
Слайд 7Доказательство:
а
с
в1
в
β
α
В
1 случай. а, в, с α рассмотрен в
2 случай. а, в α; а, с β
1. Возьмем т.В, В в
Через т.В и с проведем плоскость
α = в1
2. Если в1 β = Х, Х а, в1 α,
но Х с, т.к. в1 , а т.к. а с в1 β
3. в1 α, в1 а в1 а в1 = в (А параллельных прямых)
4. в с
Теорема доказана.
•
Две прямые, параллельные третьей прямой, параллельны
Слайд 8Теорема о параллельных прямых.
К
a
b
Дано: К a
Доказать:
! b: К
Доказательство:
1.Проведем через прямую a и точку К плоскость α.
2.Проведем через т. К α прямую b, b a.(А планиметрии)
Единственность (от противного)
1.Пусть b1: К b1 , b1 a .Через прямые a и b1 можно провести плоскость α1.
2. a , К α1; α1 и α (Т о точке и прямой в пространстве).
3. b = b1 (А параллельных прямых). Теорема доказана.
Слайд 9Задание 1 Вставьте пропущенные слова
Единственную плоскость можно задать через
2) Если точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости.
3) Две различные плоскости могут иметь только одну общую
4) Прямые являются в пространстве, если они не пересекаются и в одной плоскости.
5) Если прямая a лежит в плоскости α, прямая b не лежит в плоскости α, но пересекает ее в точке
В
α, то прямые а и b
не лежат
две
прямую
параллельными
лежат
скрещивающиеся
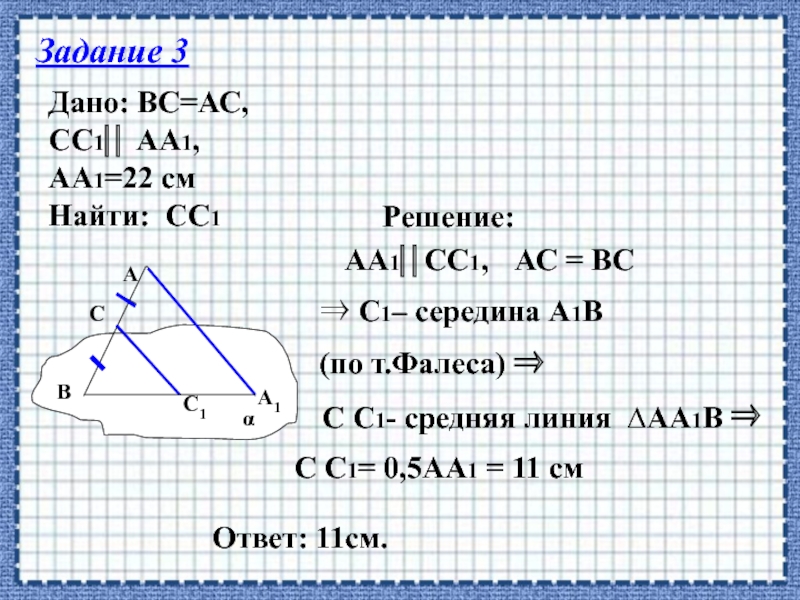
Слайд 12Задание 3
Дано: ВС=АС,
СС1 АА1,
АА1=22 см
Найти: СС1
Решение:
АА1СС1,
АС =
С1– середина А1В
(по т.Фалеса)
С С1- средняя линия ∆АА1В
С С1= 0,5АА1 = 11 см
Ответ: 11см.
Слайд 14Если прямая, не лежащая в данной плоскости,
параллельна какой-нибудь прямой,
лежащей в
она параллельна и самой плоскости.
Дано:
Доказать:
Слайд 151.Через прямые a и b проведем плоскость α
Пусть
α
2. α β = b
Если a β = Х, то Х b, это невозможно, т.к. α b
a β
a β
Теорема доказана.
Слайд 16Дано: а α
а β; β ∩ α = в
Доказать:
Доказательство:
а, в β
Пусть в ∩ а, тогда а ∩ α,
что противоречит условию.
Значит в а
Задание 2
α
β
а
в
Слайд 17A
В
С
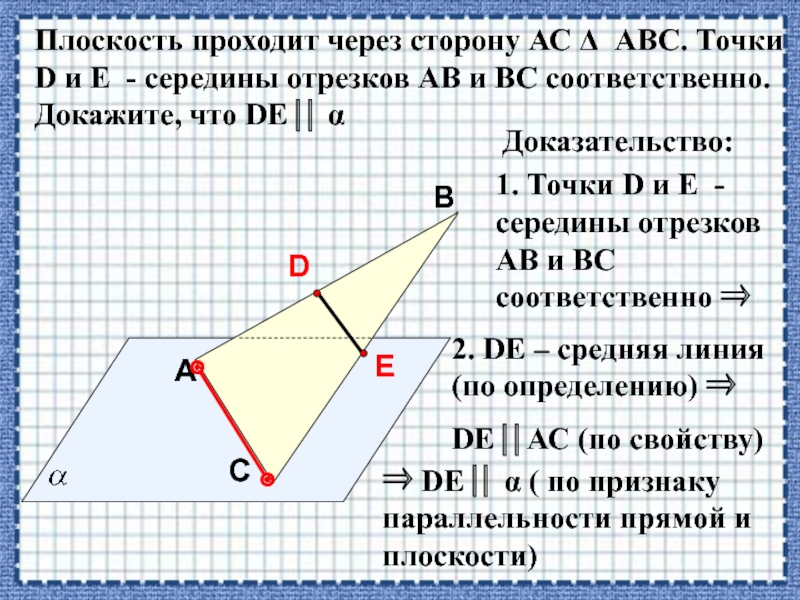
Плоскость проходит через сторону АС АВС. Точки D и E
Доказательство:
1. Точки D и E - середины отрезков АВ и BC соответственно
2. DE – средняя линия (по определению)
DE АС (по свойству)
DE α ( по признаку параллельности прямой и плоскости)
Слайд 19Признак параллельности двух плоскостей.
Если две пересекающиеся прямые одной
плоскости соответственно параллельны
пересекающимся прямым другой плоскости, то эти
плоскости параллельны.
Дано: а b = M, a , b .
a₁ b₁, a₁ , b₁ . a a₁, b b₁.
Доказать:
а
а₁
b
b₁
M
c
Доказательство:
Тогда а , а , = с, значит а с.
2. b , b , = с, значит b с.
3. Имеем, что через точку М проходят две прямые а и b, параллельные прямой с, чего быть на может.
Значит .
1. Пусть = с.
Слайд 20Теорема
Через точку вне данной плоскости можно провести плоскость, параллельную данной, причём
β
а1
•
А
α
плоскость α,
в1
в
а
Доказать:
Доказательство.
Дано:
точка А вне плоскости α.
существует плоскость β║α, проходящая через точку А
1. В плоскости α проведём прямые а∩в.
Через точку А проведём
а1║а
и в1║в.
По признаку параллельности плоскостей прямые а1 и в1 задают плоскость β║α.
Существование плоскости β доказано.
Слайд 21β
•
А
α
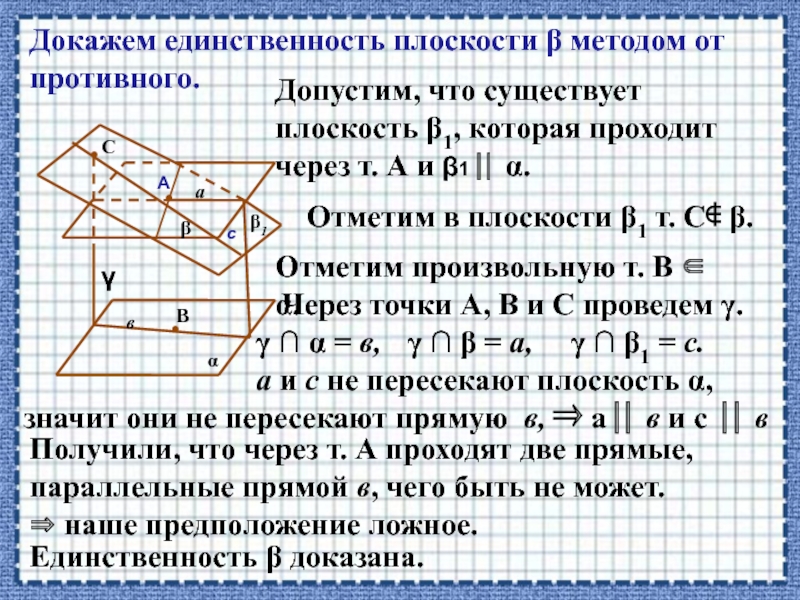
Докажем единственность плоскости β методом от противного.
•
С
•
В
в
с
β1
Допустим, что существует плоскость
Отметим в плоскости β1 т. С β.
Отметим произвольную т. В α.
Через точки А, В и С проведем γ.
γ ∩ α = в,
γ ∩ β1 = с.
γ ∩ β = а,
а
а и с не пересекают плоскость α,
значит они не пересекают прямую в,
а в и с в
Получили, что через т. А проходят две прямые, параллельные прямой в, чего быть не может.
наше предположение ложное.
Единственность β доказана.
Слайд 22Если две параллельные плоскости
пересечены третьей, то линии их пересечения параллельны.
Свойство параллельных плоскостей.
Дано:
α β, α = a
β = b
Доказать: a b
Доказательство:
1. a , b
2. Пусть a b,
тогда a b = М
3. M α, M β
α β = с (А2)
Получили противоречие с условием.
Значит a b ч. т.д.
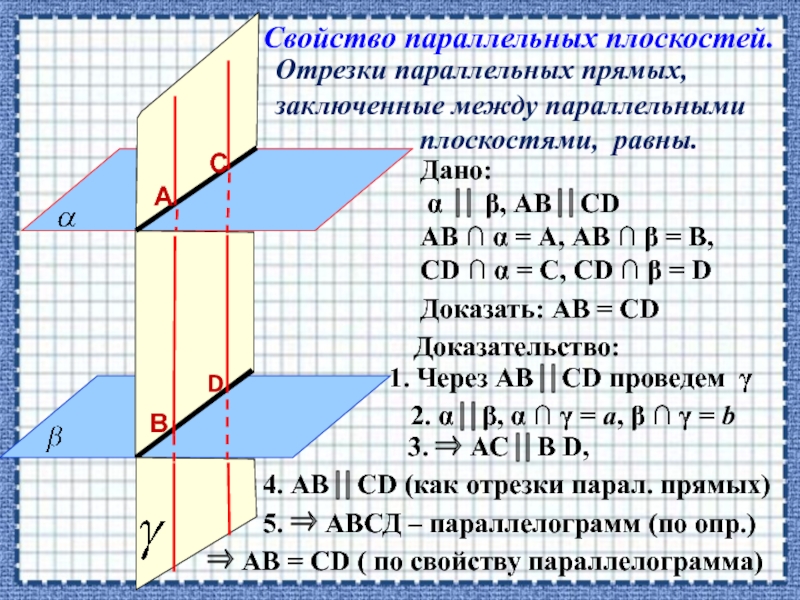
Слайд 23Отрезки параллельных прямых,
заключенные между параллельными
Свойство параллельных плоскостей.
Доказать: АВ = СD
Дано:
α β, АВ СD
АВ α = А, АВ β = В,
СD α = С, СD β = D
Доказательство:
1. Через АВ СD проведем
2. α β, α = a, β = b
3. АС В D,
4. АВ СD (как отрезки парал. прямых)
5. АВСД – параллелограмм (по опр.)
АВ = СD ( по свойству параллелограмма)
Слайд 241. если плоскости не пересекаются, то они параллельны.
2. плоскости параллельны, если
одной плоскости, параллельна другой плоскости?
3. если две прямые, лежащие в одной плоскости, параллельны двум прямым другой плоскости,
то эти плоскости параллельны?
4. если прямая перпендикулярна одной из двух параллельных плоскостей, то она
перпендикулярна и другой плоскости.
5. прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны.
6. Если прямая пересекает одну из двух плоскостей, то
она пересекает и другую.
7. Две плоскости, параллельные третьей, параллельны.
8. Отрезки прямых, заключенные между
параллельными плоскостями, равны.
Определите: верно, ли утверждение?
ДА
НЕТ
ДА
НЕТ
ДА
НЕТ
НЕТ
ДА
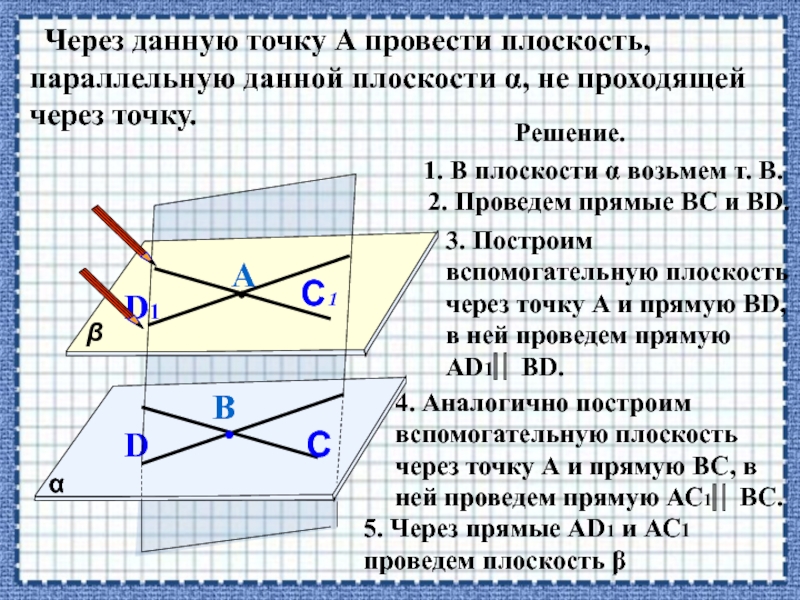
Слайд 25 Через данную точку А провести плоскость, параллельную данной плоскости α,
α
β
А
Решение.
1. В плоскости α возьмем т. В.
2. Проведем прямые ВС и ВD.
В
•
С1
D1
D
С
3. Построим вспомогательную плоскость через точку А и прямую ВD, в ней проведем прямую АD1 ВD.
4. Аналогично построим вспомогательную плоскость через точку А и прямую ВС, в ней проведем прямую АС1 ВС.
•
5. Через прямые АD1 и АС1 проведем плоскость β
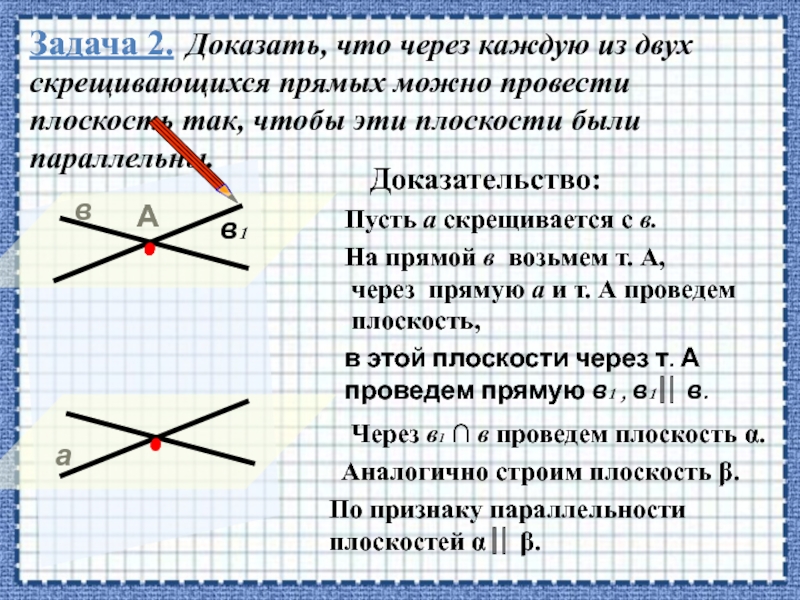
Слайд 26Задача 2. Доказать, что через каждую из двух скрещивающихся прямых можно
а
в
Пусть а скрещивается с в.
Доказательство:
На прямой в возьмем т. А,
А
через прямую а и т. А проведем плоскость,
в этой плоскости через т. А проведем прямую в1 , в1 в.
Через в1 в проведем плоскость α.
.
в1
Аналогично строим плоскость β.
По признаку параллельности плоскостей α β.
.