Работа учителя математики
МБОУ «Малокибечская ООШ им.А.Я.Яковлева » Канашского района Чувашской Республики Моисеевой Людмилы Геннадьевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Золотое сечение и золотая спираль - кривая жизни
Содержание
- 1. Презентация по математике Золотое сечение и золотая спираль - кривая жизни
- 2. Цель: исследование роли золотого сечения и золотой
- 3. Методы исследованияметод анализа научных источников, метод наблюдение, метод анкетирование, практические измерения и вычисления.
- 4. СодержаниеОснователи учения о
- 5. Слайд 5
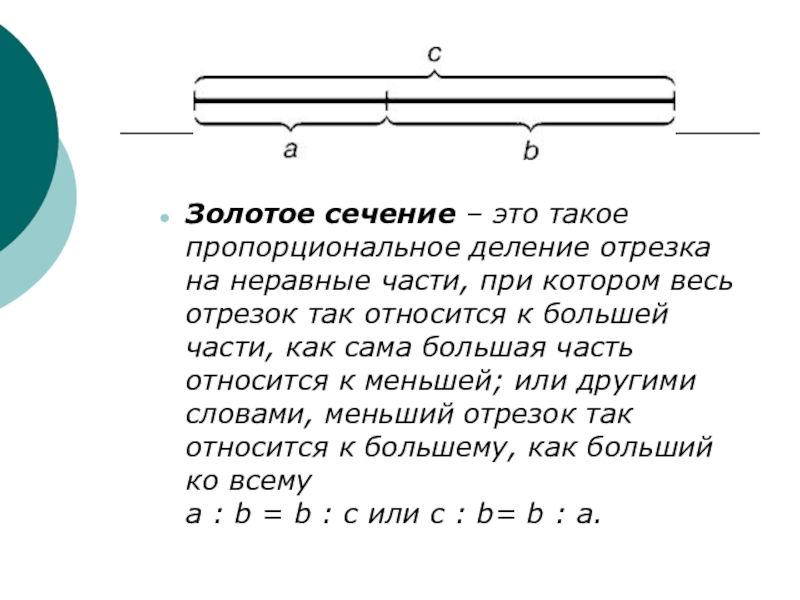
- 6. Золотое сечение – это такое пропорциональное деление
- 7. Слайд 7
- 8. Основатели золотого сеченияПонятие золотого сечения ввел Пифагор.Термин
- 9. Золотое сечение в природе.Белорусский ученый
- 10. Еще Архимед, уделяя внимание спирали, вывел на
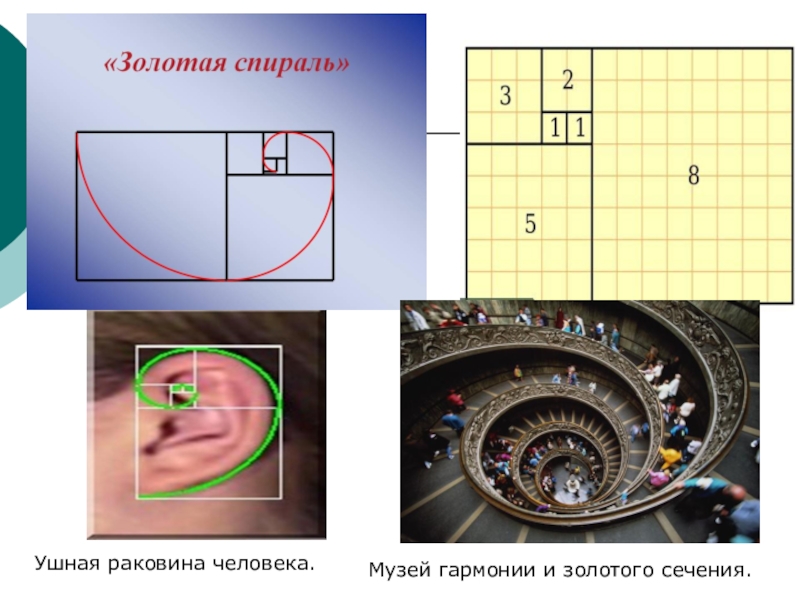
- 11. .Cпираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т. д.
- 12. Ушная раковина человека.Музей гармонии и золотого сечения.
- 13. Паук плетет паутину спиралеобразно.Спиральная галактика.Ураган закручивается спиралью.
- 14. Слайд 14
- 15. Золотые пропорции в теле человека.
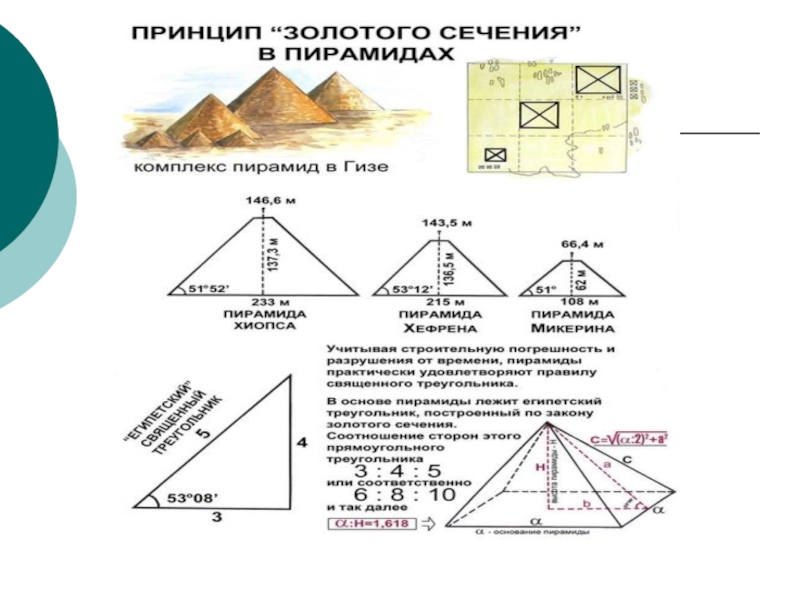
- 16. Золотое сечение в архитектуре.
- 17. число фидия Число
- 18. Числа фибоначи «Золотое сечение» сязана
- 19. Размеры многих храмов Новгорода определены в частях и в целом как соразмерности золотого сечения
- 20. Слайд 20
- 21. Храм Василия Блаженного
- 22. Золотое сечение в живописи.Портрет Монны Лизы (Джоконды)
- 23. И.И. Шишкин. "Сосновая роща" На этой знаменитой
- 24. Золотое сечение в картине И.И.Шишкин. «Сосновая роща».
- 25. Зрительные центры картиныЕще в эпоху ВозрожденияЕще в
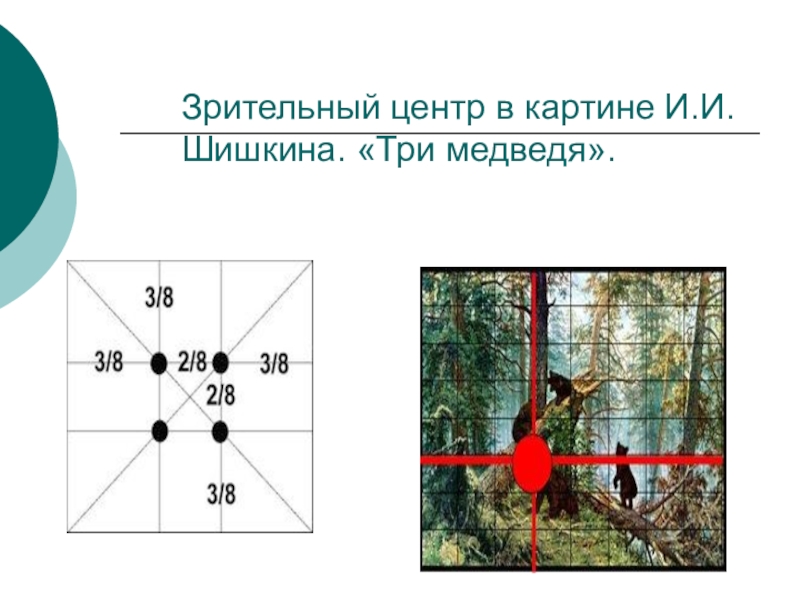
- 26. Зрительный центр в картине И.И.Шишкина. «Три медведя».
- 27. Золотая спираль в картине Рафаэля"Избиение младенцев"
- 28. Правило золотого сечения в произведениях русской классики.
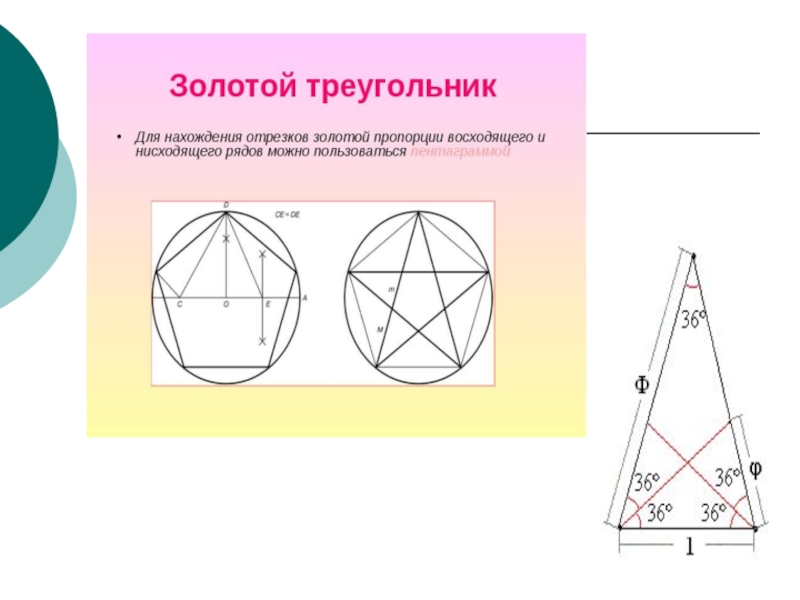
- 29. Пентаграмма.В пентаграмме каждая из
- 30. Пятиконечная звезда на флагах многих стран мира.
- 31. Слайд 31
- 32. Слайд 32
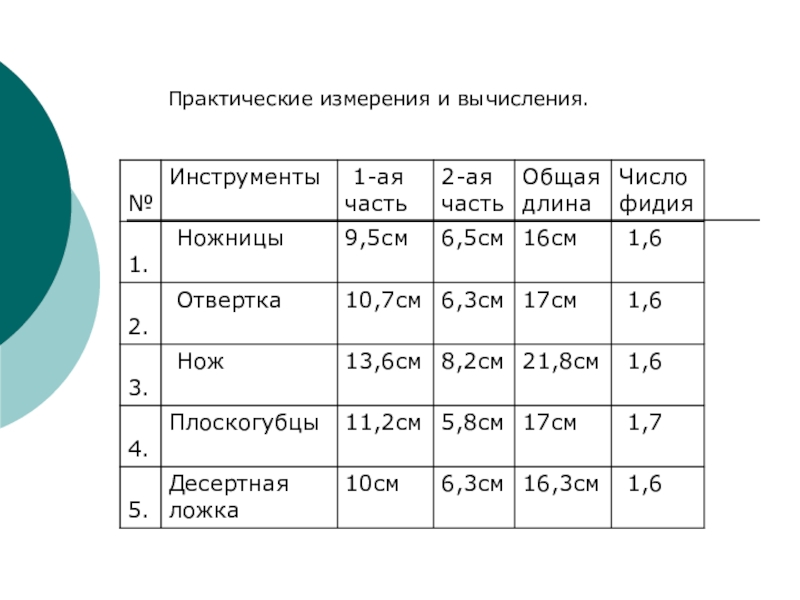
- 33. Практические измерения и вычисления.
- 34. Список используемой литературыА.В. Волошинов. Пифагор.- М: «Просвещение»
Цель: исследование роли золотого сечения и золотой спирали в жизни человека.Задачи: Изучить научную и историческую литературу о золотом сечении и золотой спирали.Исследовать как золотое сечение и золотая спираль славятся произведениями искусства, архитектуры, живописи.Выяснить золотое сечение в
Слайд 2Цель: исследование роли золотого сечения и золотой спирали в жизни человека.
Задачи:
Изучить научную и историческую литературу о золотом сечении и золотой спирали.
Исследовать как золотое сечение и золотая спираль славятся произведениями искусства, архитектуры, живописи.
Выяснить золотое сечение в инструментах быта.
Исследовать как золотое сечение и золотая спираль славятся произведениями искусства, архитектуры, живописи.
Выяснить золотое сечение в инструментах быта.
Слайд 3Методы исследования
метод анализа научных источников,
метод наблюдение,
метод анкетирование,
практические измерения
и вычисления.
Слайд 4 Содержание
Основатели учения о золотом сечении
Понятие золотого сечения
Золотое сечение в природе
Золотое сечение в архитектуре
Золотое сечение в живописи Золотое сечение в живописи
Пентаграмма
Золотое сечение вокруг нас
Список используемой литературы
Слайд 6Золотое сечение – это такое пропорциональное деление отрезка на неравные части,
при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b = b : c или с : b= b : а.
Слайд 8Основатели золотого сечения
Понятие золотого сечения ввел Пифагор.
Термин «золотое сечение»-Леонардо да Винчи
Леонардо
да Винчи
(1452-1519)
(1452-1519)
Пифагор Самосский
(570-490г.до н.э.)
Слайд 9 Золотое сечение в природе.
Белорусский ученый Эдуард Сороко, который изучал
формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.
Слайд 10Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение,
которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи
Слайд 11.Cпираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах
и т. д.
Слайд 15Золотые пропорции в теле человека.
В 1855 г. немецкий
исследователь золотого сечения В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд "Эстетические исследования"
Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа - важнейший показатель золотого сечения Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа - важнейший показатель золотого сечения. Пропорции мужского тела колеблются пределах среднего отношения и несколько ближе подходят к золотому сечению Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа - важнейший показатель золотого сечения. Пропорции мужского тела колеблются пределах среднего отношения и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела - длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа - важнейший показатель золотого сечения Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа - важнейший показатель золотого сечения. Пропорции мужского тела колеблются пределах среднего отношения и несколько ближе подходят к золотому сечению Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа - важнейший показатель золотого сечения. Пропорции мужского тела колеблются пределах среднего отношения и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела - длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Слайд 17 число фидия
Число PHI - самое красивое и
совершенное число в мире, к такому заключению пришло большинство ученых. Это число еще называют "золотым сечением" или "Ф", в честь древнегреческого скульптора Фидия, который первым смог использовать число PHI в своих скульптурах.
Число PHI равно 1.618, оно было получено из последовательности учений Фибоначчи. Особенность его последовательности заключается в том, что каждый третий член равен сумме двух предыдущих членов, а частное двух соседствующих чисел наделено уникальным свойством иметь приближенность к числу 1.618, оно же и есть число PHI.
Число PHI равно 1.618, оно было получено из последовательности учений Фибоначчи. Особенность его последовательности заключается в том, что каждый третий член равен сумме двух предыдущих членов, а частное двух соседствующих чисел наделено уникальным свойством иметь приближенность к числу 1.618, оно же и есть число PHI.
Слайд 18 Числа фибоначи
«Золотое сечение» сязана с рядом фибоначчи: 1,
1, 2, 3, 5, 8, 13, 21, 34, ..
1:1=1, 2:1=2, 3:2=1,5, 5:3=1,666...,21:13=1,615384...,если так продолжим в пределе получаем 1,618034... бесконечное число- фидия Ф=1,618034... и так далее ...
Слайд 19Размеры многих храмов Новгорода определены в частях и в целом как
соразмерности золотого сечения
Слайд 22Золотое сечение в живописи.
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание
исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника.
Слайд 23И.И. Шишкин. "Сосновая роща"
На этой знаменитой картине И. И. Шишкина с
очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен - при желании можно с успехом продолжить деление картины по золотому сечению и дальше.
Слайд 25Зрительные центры картины
Еще в эпоху ВозрожденияЕще в эпоху Возрождения художники открыли,
что любая картинаЕще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картинаЕще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина - горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.
Слайд 28Правило золотого сечения в произведениях русской классики.
Кульминационным моментом «Пиковой
дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) – это и есть точка золотого сечения.
Слайд 29 Пентаграмма.
В пентаграмме каждая из пяти линий, составляющих эту
фигуру, делит другую в отношении золотого сечения, а концы звезды являются золотыми треугольниками
Слайд 34Список используемой литературы
А.В. Волошинов. Пифагор.- М: «Просвещение» 1993 г.
Г.И. Глейзер. История
математики в школе VII-VIII кл. Пособие для учителей.- М: «Просвещение» 1982 г.
Лиман М.М. Школьникам о математике и математиках. М: «Просвещение» 1981 г.
www photoline.ru/tcomp 1.htm.
http//www.nips.riss-telecom.ru/poly/
Лиман М.М. Школьникам о математике и математиках. М: «Просвещение» 1981 г.
www photoline.ru/tcomp 1.htm.
http//www.nips.riss-telecom.ru/poly/