- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Учись применять математику
Содержание
- 1. Презентация по математике Учись применять математику
- 2. Где применяется математика?Математическая грамотность, состоящая в умении применять математику для решения жизненных задач, нужна всем.
- 3. Как применяется математика?В основе применения математики к
- 4. Как применяется математика?1 этап. Перевод задачи на
- 5. Задача . Необходимо закупить кафельную плитку размерами
- 6. 1 этап. Перевод задачи на язык математики.
- 7. 2 этап. Решение математической задачи. 220: 20=11
- 8. 3 этап. Осмысление полученного решения. Нужно найти
- 9. 1. Сколько квадратных плиток размерами 10 см
- 10. Поиски неизвестного количества.Задача 1. Малышу 1 января
- 11. Анализируем. Малыш - 7 конфет
- 12. Задача 2. Малыш и Карлсон принимали участие
- 13. Анализируем.Рассмотрим два случая – Малыш сзади Карлсона
- 14. Задача 3. Чтобы оградить участок квадратной формы,
- 15. Анализируем. Изобразим участок в виде квадрата .Так
- 16. Задача 4. Купили 7 книг по математике,
- 17. Анализируем. Из условия задачи вытекает, что купили
- 18. Задача 5. Имеются брёвна длиной 4 м
- 19. Анализируем. Чтобы, например, из 4-метрового бревна получить
- 20. Задача 6. Чтобы подняться с первого этажа
- 21. Анализируем. Подняться на третий этаж – это
- 22. Литература: Бродский Я. С., Павлов А. Л.
Слайд 2Где применяется математика?
Математическая грамотность, состоящая в умении применять математику для решения
Слайд 3Как применяется математика?
В основе применения математики к решению различных задач лежит
Слайд 4Как применяется математика?
1 этап. Перевод задачи на язык математики
2 этап. Решение математической задачи.
3 этап. Осмысление полученного решения, его применение для решения исходной задачи.
Слайд 5Задача . Необходимо закупить кафельную плитку размерами 20 см 20
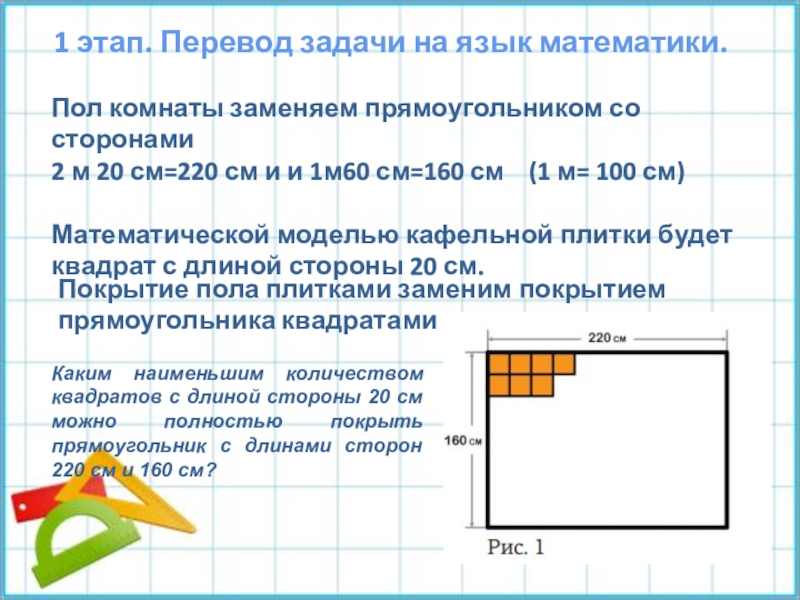
Слайд 61 этап. Перевод задачи на язык математики.
Пол комнаты заменяем прямоугольником
2 м 20 см=220 см и и 1м60 см=160 см (1 м= 100 см)
Математической моделью кафельной плитки будет квадрат с длиной стороны 20 см.
Покрытие пола плитками заменим покрытием прямоугольника квадратами
Каким наименьшим количеством квадратов с длиной стороны 20 см можно полностью покрыть прямоугольник с длинами сторон 220 см и 160 см?
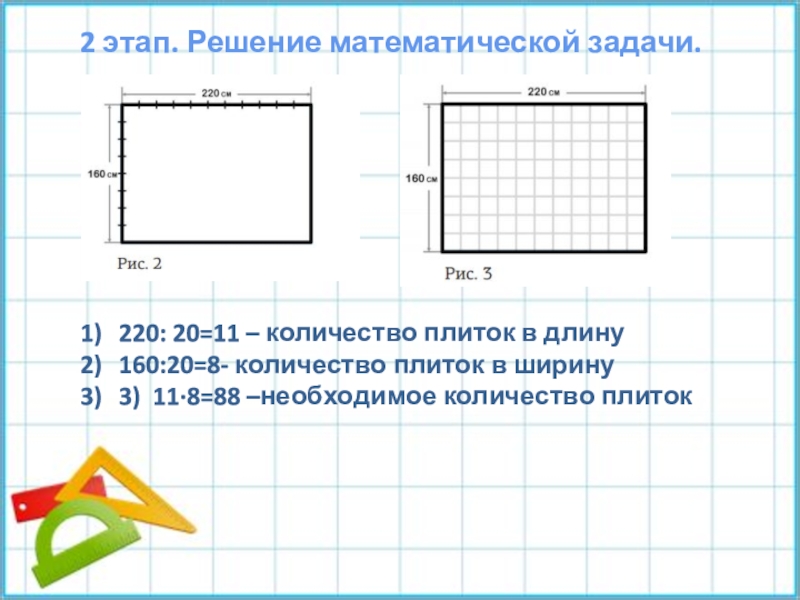
Слайд 72 этап. Решение математической задачи.
220: 20=11 – количество плиток в
160:20=8- количество плиток в ширину
3) 11∙8=88 –необходимое количество плиток
Слайд 83 этап. Осмысление полученного решения.
Нужно найти количество упаковок кафеля. В
Так как при делении на 10 числа 88 в частном получается 8 и в остатке 8, то число упаковок равно 8 + 1 = 9.
Действительно, 8 упаковок недостаточно: 810 = 80, что меньше 88, а 910 = 90. Следовательно, нужно купить
9 упаковок.
Слайд 91. Сколько квадратных плиток размерами 10 см u10 см потребуется для
А. 200. Б. 20. В. 100. Г. 2 000.
1.A.
2. Сколько квадратных плиток размерами 10 см u10 см потребуется для того, чтобы покрыть прямоугольный участок стены размерами
1 м 15 см u 2 м?
А. 230. Б. 240. В. 2 000. Г. 2 200.
Проверь себя.
2.Б.
Слайд 10Поиски неизвестного количества.
Задача 1. Малышу 1 января 2010 года подарили мешок
(1 января 2010 года – пятница).
Слайд 11Анализируем.
Малыш - 7 конфет
Карлсон
На сколько воскресений хватило конфет?
Сколько было конфет(313) и сколько их съедали за неделю (9)?
Решаем.
313 : 9 = 34 (остаток 7).
Конфет хватило на 34 недели и ещё на несколько дней. Так как эти несколько дней начинаются с пятницы и на них осталось 7 конфет, то ещё одно воскресенье Карлсон получал конфеты. Следовательно, он получал конфеты 35 воскресений и съел 352 = 70 конфет.
Ответ. 70 конфет.
Слайд 12Задача 2. Малыш и Карлсон принимали участие в легкоатлетическом забеге в
В некоторый момент оказалось, что трое впереди Малыша, а сзади Карлсона – четверо. Сколько в этот момент человек находилось между Карлсоном и Малышом, если никто из бегущих не находился рядом друг с другом?
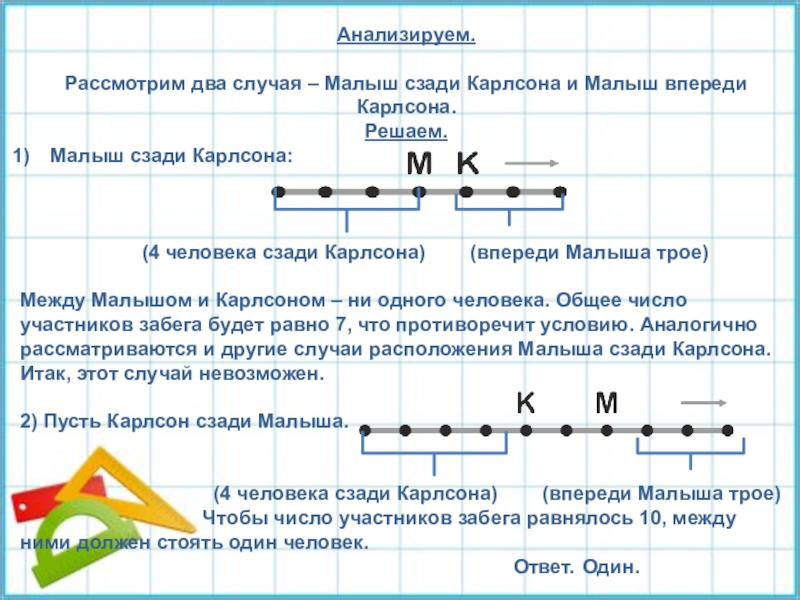
Слайд 13Анализируем.
Рассмотрим два случая – Малыш сзади Карлсона и Малыш впереди Карлсона.
Решаем.
Малыш
(4 человека сзади Карлсона) (впереди Малыша трое)
Между Малышом и Карлсоном – ни одного человека. Общее число участников забега будет равно 7, что противоречит условию. Аналогично рассматриваются и другие случаи расположения Малыша сзади Карлсона. Итак, этот случай невозможен.
2) Пусть Карлсон сзади Малыша.
(4 человека сзади Карлсона) (впереди Малыша трое)
Чтобы число участников забега равнялось 10, между ними должен стоять один человек.
Ответ. Один.
Слайд 14Задача 3. Чтобы оградить участок квадратной формы, нужно вдоль каждой стороны
Слайд 15
Анализируем.
Изобразим участок в виде квадрата .
Так как на каждой стороне
и два из них на её концах, то между концами
каждой стороны (между соседними
вершинами квадрата!) стоит по 6 столбов.
А кроме того, 4 столба стоят по углам участка.
Решаем.
64 = 24 столба.
По углам участка должны стоять столбы. Значит, требуется ещё 4 столба.
24 + 4 = 28 столбов.
Ответ. 28 столбов.
Слайд 16Задача 4. Купили 7 книг по математике, информатике и истории. Сколько
Слайд 17Анализируем.
Из условия задачи вытекает, что купили различное число книг по
Для решения задачи число 7 нужно представить в виде суммы трёх различных натуральных чисел.
Решаем.
Так как число 7 единственным образом можно представить в виде суммы трёх различных натуральных чисел: 7 = 1 + 2 + 4, то больше всего купили книг по информатике – 4, по истории – 2 и одну по математике.
Ответ. Купили одну книгу по математике, 2 – по истории, 4 – по информатике.
Слайд 18Задача 5. Имеются брёвна длиной 4 м и 5 м ,
5-метровые брёвна. Какие брёвна надо пилить, чтобы выполнить работу за кратчайшее время?
Слайд 19Анализируем.
Чтобы, например, из 4-метрового бревна получить 4 столбика длиной 1
Решаем.
4-метровые брёвна:
20:4 = 5 брёвен
35 = 15 распилов
115 = 15 мин.
5-метровые брёвна:
20:5 = 4 бревна
44 = 16 распилов
116 = 16 мин.
Так как 15 мин меньше 16 мин, то пилить
надо 4-метровые брёвна.
Ответ. 4-метровые бревна.
Слайд 20Задача 6. Чтобы подняться с первого этажа на третий этаж дома,
Слайд 21Анализируем.
Подняться на третий этаж – это значит преодолеть два этажа:
Далее можно найти, сколько этажей надо преодолеть, чтобы подняться на шестой этаж и сколько пройти при этом ступенек.
Решаем.
Чтобы преодолеть один этаж, нужно пройти 48:2 = 24 ступеньки.
Чтобы подняться на шестой этаж, надо преодолеть 6 – 1 = 5 этажей и при этом пройти 245 = 120 ступенек.
Ответ. 120 ступенек.