- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике: Применение производной к исследованию функции
Содержание
- 1. Презентация по математике: Применение производной к исследованию функции
- 2. «Мало иметь хороший ум, главное -хорошо его применять».Р.Декарт
- 3. Слайд 3
- 4. Признак возрастания: Если f′(х) > 0 в
- 5. ПРИМЕР 1: Найдем промежутки возрастания и убывания
- 6. Необходимое условие экстремума: Если точка Хо является
- 7. Точки максимума и минимума функции
- 8. ПРИМЕР 2: Исследуем функцию f(x) =
- 9. Наибольшее или
- 10. ПРИМЕР 3: Найдем наибольшее и наименьшее значение
- 11. Изложенный выше метод поиска наибольших и наименьших значений применим к решению разнообразных прикладных задач.
- 12. ПРИМЕР 4: Число 24 представьте в виде
- 13. «Считай несчастным тот день и тот час,
- 14. Спасибо за внимание!
Слайд 1Применение производной к исследованию функции
Разработчик:
Веремеенко Т.Н
1 курс
Алгебра и начала анализа
Слайд 3 Понятие производной тесно
Слайд 4Признак возрастания: Если f′(х) > 0 в каждой точке интервала, то
Признак убывания: Если f′(х) < 0 в каждой точке интервала, то функция убывает на этом интервале.
Одна из основных задач исследования функции- это нахождение промежутков её возрастания и убывания.
Слайд 5ПРИМЕР 1: Найдем промежутки возрастания и убывания функции f(x) = x3–5x2–32х+9.
РЕШЕНИЕ:
1)
Д=484>0, два корня х1 = – 2, х2 = 16/3 = 5⅓
3) Устанавливаем знак производной на каждом интервале.
Ответ: функция возрастает на каждом из промежутков (– ∞; –2] и [5⅓; +∞),
убывает на промежутке[–2; 5⅓]
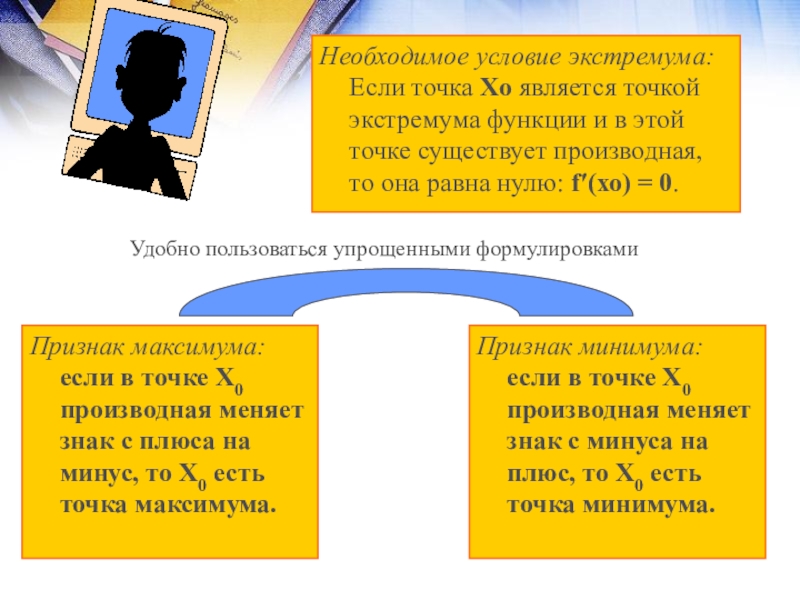
Слайд 6Необходимое условие экстремума: Если точка Хо является точкой экстремума функции и
Признак максимума: если в точке X0 производная меняет знак с плюса на минус, то Х0 есть точка максимума.
Признак минимума: если в точке Х0 производная меняет знак с минуса на плюс, то Х0 есть точка минимума.
Удобно пользоваться упрощенными формулировками
Слайд 7
Точки максимума и минимума функции f(x) называют точками её
а значение функции в этих точках – экстремумами функции.
Слайд 8
ПРИМЕР 2: Исследуем функцию f(x) = x3–3x на экстремум.
РЕШЕНИЕ:
1) Находим
2) Критические точки: 3x2–3 = 0; x2 –1=0,
следовательно х1= 1, х2= –1
3)производная на интервале (– ∞; –1) имеет знак плюс, на интервале (–1; 1) знак минус,
следовательно точка х = –1 – точка максимума.
Аналогично выясняем, что х = 1 – точка минимума
4) Вычислим значение функции в этих точках:
f(–1) = (–1)3–3(–1) = 2 f(1) = 13–3·1 =–2
Ответ: max f(–1) = 2; min f(1) = –2
Слайд 9 Наибольшее или наименьшее значение функции, непрерывной
Находят критические точки на этом промежутке.
Вычисляют значение функции в критических точках и на концах данного промежутка.
Из всех полученных значений выбирают наибольшее или наименьшее.
Слайд 10ПРИМЕР 3: Найдем наибольшее и наименьшее значение функции: f(x) =6x3–3x2–12x+7 на отрезке
РЕШЕНИЕ:
Находим критические точки заданной функции f′(x) = 18x2–6x–12;
18x2–6x–12 = 0/: 6
3x2–x–2 = 0; х1 = 1; х2 = –2/3 ∉ [0;2]
2) Вычислим значения функции на концах заданного отрезка и в точке х =1:
f(0) = 7;
f(1) = 6-3-12+7= -2;
f(2) = 48-12-24+7=19
из полученных значений выбираем наименьшее и наибольшее
Ответ: наименьшее f(1) = -2, наибольшее f(2) = 19
Слайд 11
Изложенный выше метод поиска наибольших и наименьших значений применим к решению
Слайд 12
ПРИМЕР 4: Число 24 представьте в виде суммы двух неотрицательных слагаемых
РЕШЕНИЕ:
1) Пусть первое число х, тогда второе (24-х).
2) Сумму квадратов выразим через функцию:
f(x) = х2+(24-х)2 при х ∈ [0; 24]
f (x) = х2+576–48х+х2;
f(x) = 2х2–48х+576;
3) Найдем производную f′(x) = 4х–48 и приравняем к нулю:4х–48 = 0,
Х = 12 – критическая точка.
4) Найдем значение функции в критической точке и на концах отрезка:
f(0) = 576; f(12) = 288;f(24) = 576
Следовательно, наименьшее значение функция имеет при х=12.
Ответ: 24=12+12
Слайд 13«Считай несчастным тот день и тот час, в который ты не
Я.А.Коменский







![Презентация по математике: Применение производной к исследованию функции Наибольшее или наименьшее значение функции, непрерывной на промежутке Наибольшее или наименьшее значение функции, непрерывной на промежутке [а; в], находят по](/img/thumbs/deb9c697331587b2bfb8b73900873b40-800x.jpg)
![Презентация по математике: Применение производной к исследованию функции ПРИМЕР 3: Найдем наибольшее и наименьшее значение функции: f(x) =6x3–3x2–12x+7 на ПРИМЕР 3: Найдем наибольшее и наименьшее значение функции: f(x) =6x3–3x2–12x+7 на отрезке [0;2]РЕШЕНИЕ:Находим критические точки заданной функции](/img/thumbs/e28d6cd39f1895af648dc12740266723-800x.jpg)









