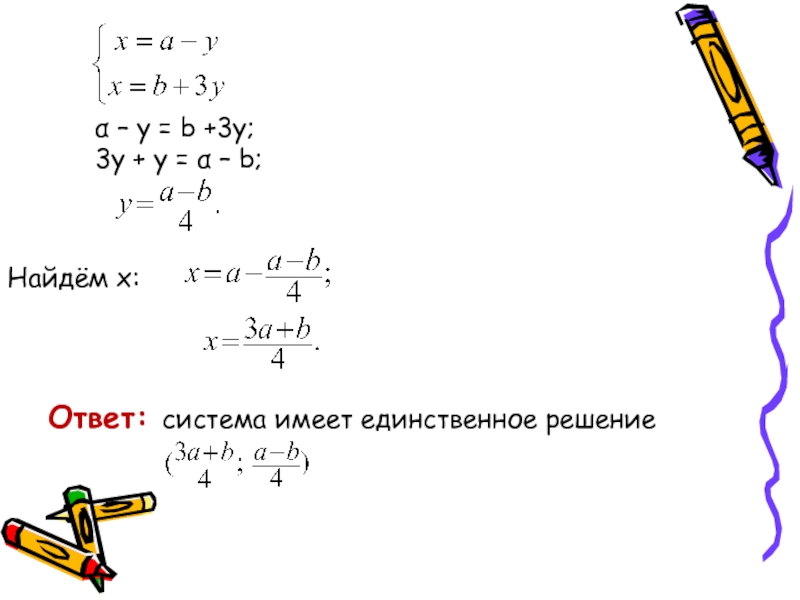Презентация, доклад по математике по теме: Подготовка 9-х классов к ОГЭ по математике по теме:Решение систем уравнений

Содержание

1. Презентация по математике по теме: Подготовка 9-х классов к ОГЭ по математике по теме:Решение систем уравнений
2. Методы решения систем уравнений:Графический Метод подстановкиМетод алгебраического сложенияМетод введения новых неизвестных
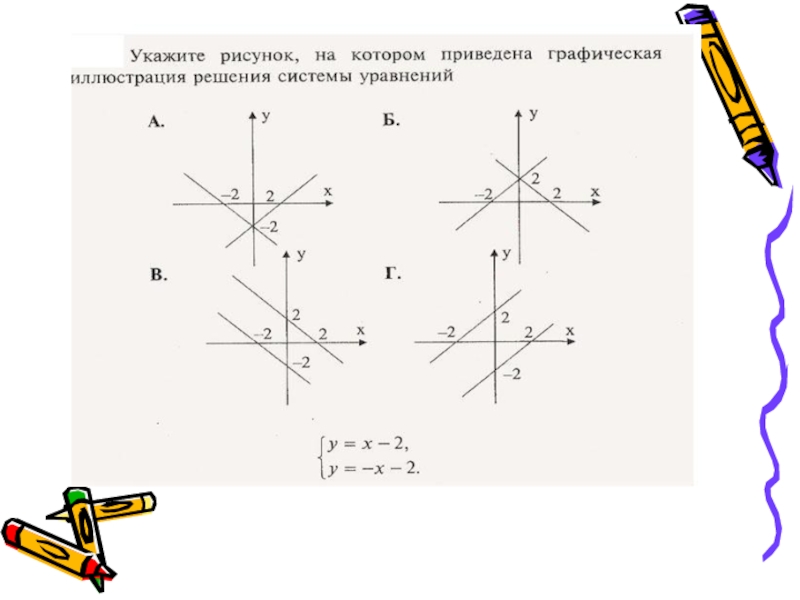
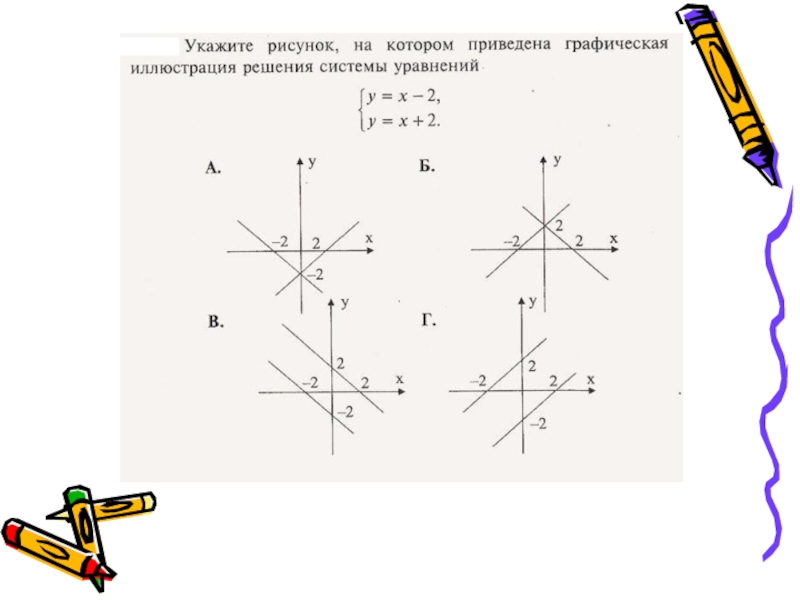
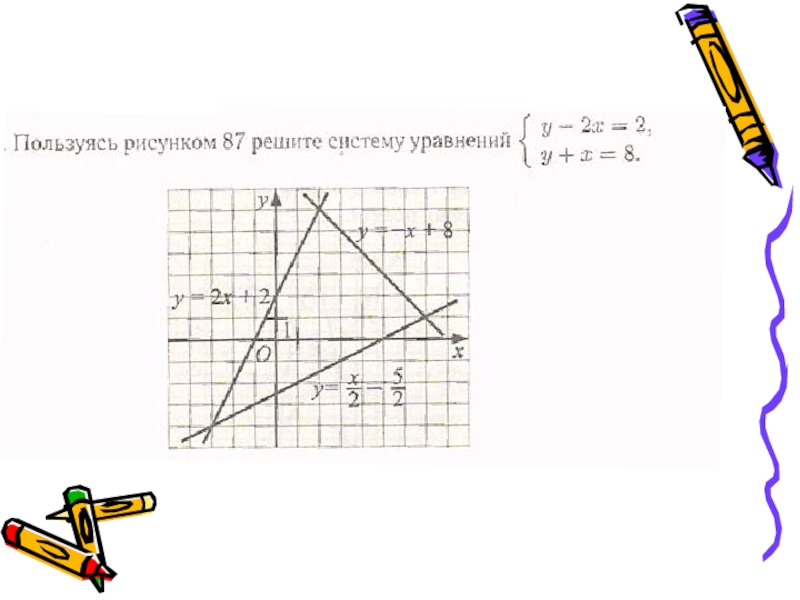
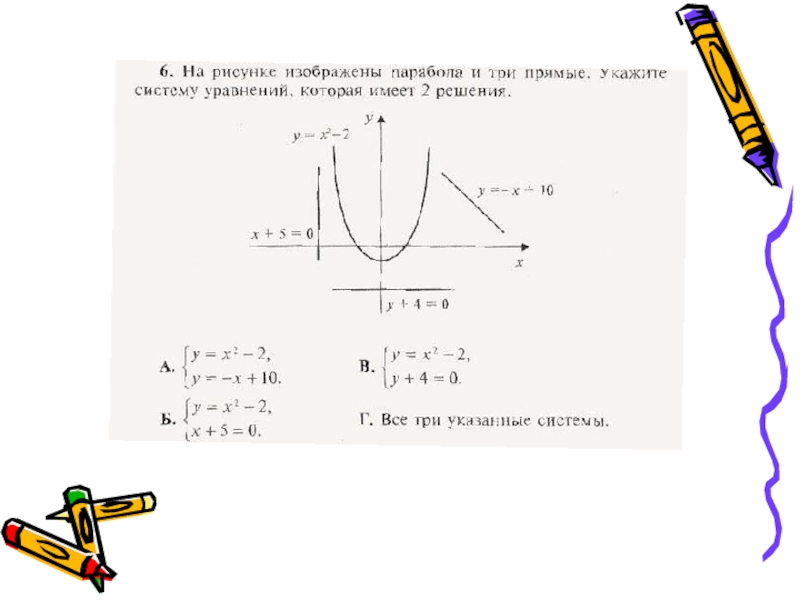
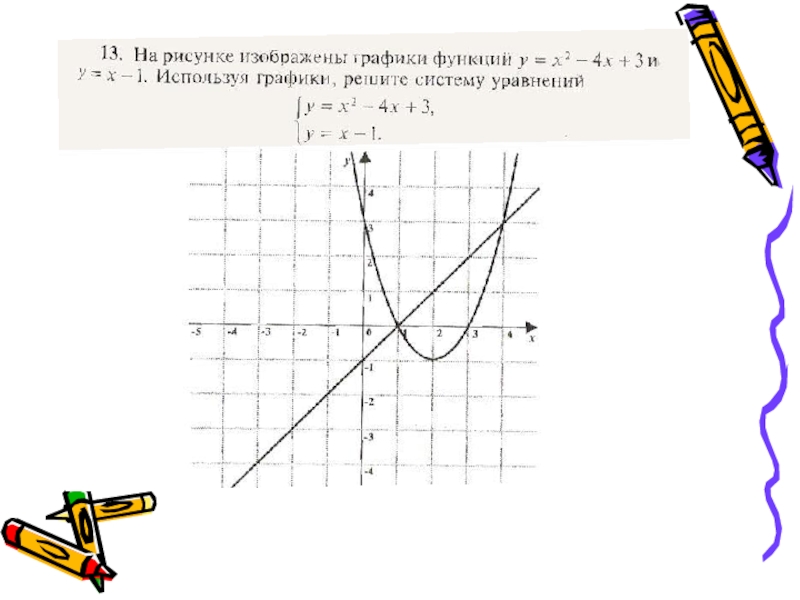
3. Графический метод решения систем уравнений
4. Слайд 4
5. Слайд 5
6. Слайд 6
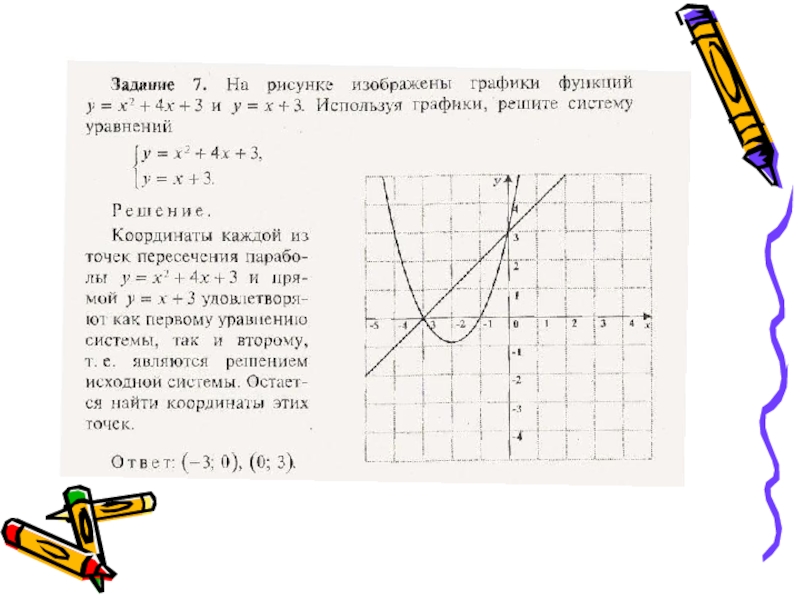
7. Слайд 7
8. Слайд 8
9. Слайд 9
10. Слайд 10
11. Слайд 11
12. Слайд 12
13. Метод подстановки
14. Решить систему уравнений
15. Слайд 15
16. Слайд 16
17. Метод введения новых неизвестных
18. Слайд 18
19. Слайд 19
20. Слайд 20
21. Слайд 21
22. Слайд 22
23. Слайд 23
24. Слайд 24
25. Слайд 25
26. Слайд 26
27. Слайд 27
28. Слайд 28
29. Метод алгебраическогосложения
30. Решить систему уравнений
31. Слайд 31
32. Слайд 32
33. Решение систем линейных уравнений(с двумя переменными) с параметрами.
34. Зависимость количества решений системы линейных
35. Пример 1. При каких
36. Заметим, что
37. Решение. Данная система уравнений – линейная.
38. Ответ: система имеет единственное решение
39. Пример 3. Графики функций у = (4
40. Слайд 40
41. Слайд 41
42. Слайд 42
43. Слайд 43
44. Слайд 44
45. Применение систем уравнений
46. Слайд 46
47. Слайд 47
48. Проверка решений системы по определению
49. Задания для зачетной работы
50. Слайд 50
51. Слайд 51
52. Слайд 52
53. Слайд 53
54. Задания повышенной сложности
55. Слайд 55
56. Слайд 56
57. Слайд 57
58. Слайд 58
59. Слайд 59

Методы решения систем уравнений:Графический Метод подстановкиМетод алгебраического сложенияМетод введения новых неизвестных

Главная
Математика
Презентация по математике по теме: Подготовка 9-х классов к ОГЭ по математике по теме:Решение систем уравнений

Слайд 1Подготовка 9-х классов к ОГЭ по математике по теме: «Решение систем уравнений»

Слайд 2Методы решения систем уравнений:
Графический
Метод подстановки
Метод алгебраического сложения
Метод введения новых неизвестных

Слайд 3Графический метод решения
систем уравнений

Слайд 13 Метод
подстановки

Слайд 14Решить систему уравнений

Слайд 17 Метод введения новых неизвестных

Слайд 29 Метод алгебраического
сложения

Слайд 30Решить систему уравнений

Слайд 33Решение систем линейных уравнений
(с двумя переменными) с параметрами.

Слайд 34
Зависимость количества решений системы линейных уравнений от коэффициента системы.

Слайд 35 Пример 1. При каких значениях параметра α система

а) имеет бесконечное множество решений;
б) имеет единственное решение?

Решение. Данная система уравнения является линейной, причём
коэффициенты первого уравнения отличны от нуля.
Воспользуемся данными схемы .

а) Система имеет бесконечный множитель решений, если

, α = 4.

б) Система имеет единственное решение, если

≠

, α ≠ 4.

Пример 1. При каких значениях параметра α система

Слайд 36 Заметим, что уравнения системы поменяли местами,

так как число α неопределённое. В нашем случае α = 0
является решением в случае б), чтобы не было недоумений с делением на нуль, лучше вторым считать то уравнение, в котором все коэффициенты определены и не равны нулю.

Ответ: если α = 4, то система имеет
бесконечное множество решений;
если α ≠ 4, то решение единственное.

Заметим, что уравнения системы поменяли местами, так как число α неопределённое. В

Слайд 37 Решение. Данная система уравнений – линейная.

Так как
≠

, то система, имеет единственное
решение.

Пример 2. Решить систему уравнений

Найдём его:

Решение. Данная система уравнений – линейная. Так как ≠ , то система, имеет единственное

Слайд 38 Ответ: система имеет единственное решение
Найдём x:
α

– у = b +3у;
3у + у = α – b;

Ответ: система имеет единственное решение Найдём x: α – у = b +3у;3у +

Слайд 39Пример 3. Графики функций у = (4 – α)x + α

и у = αx + 2
пересекаются в точке с абсциссой, равной -2.
Найдите ординату точки пересечения.
Решение. Так как графики пересекаются в точке абсциссой,
равной -2, то x = -2 является решением следующей системы:

Тогда имеем :

- 8 + 3α = -2α +2;
5α = 10;
α = 2.

Найдём ординату у, подставим x и α в любое уравнения
системы: у = 2 · (- 2) + 2, у = - 2.
Ответ: -2