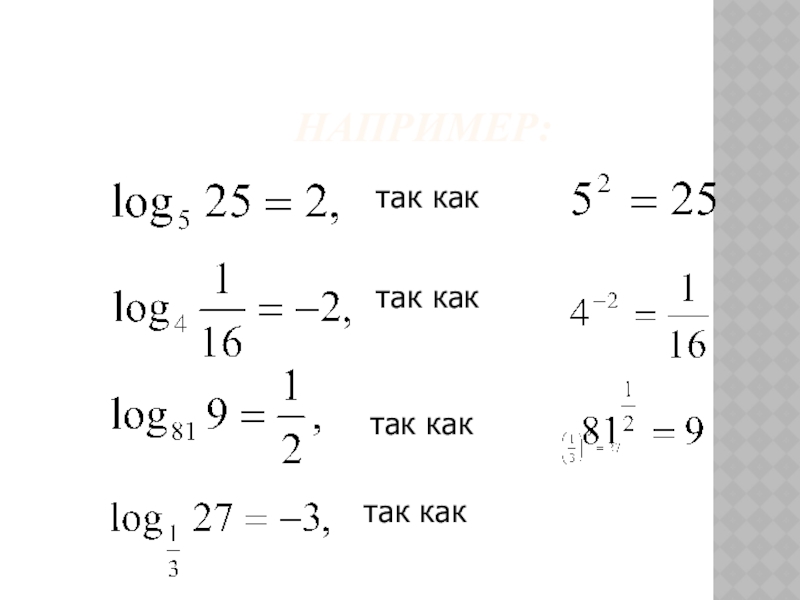- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике по теме Логарифмы
Содержание
- 1. Презентация по математике по теме Логарифмы
- 2. ЦЕЛИ УРОКАпознакомиться с понятием «логарифма числа», изучить
- 3. Свойства степеней
- 4. ДЛЯ ЧЕГО БЫЛИ ПРИДУМАНЫ ЛОГАРИФМЫ ? Как
- 5. ДЛЯ ЧЕГО БЫЛИ ПРИДУМАНЫ ЛОГАРИФМЫ ? …Если
- 6. Джон Непер(1550-1617) – английский математик. Изобретатель логарифмов,
- 7. Титульный лист книги Дж. Непера «Описание удивительной таблицы логарифмов».Издание 1620 г.
- 8. Решите уравнения:x = 3x = ??
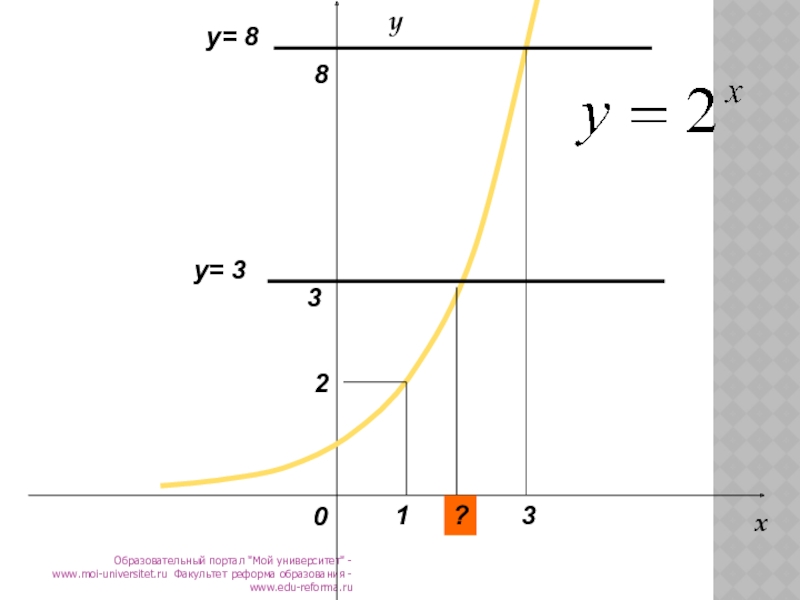
- 9. Образовательный портал "Мой университет" - www.moi-universitet.ru Факультет реформа образования - www.edu-reforma.ru0383y= 312y= 8xy?
- 10. Решите уравнения:x = 3?
- 11. ВОЗВЕДЕНИЕ В СТЕПЕНЬ ИМЕЕТ ДВА ОБРАТНЫХ ДЕЙСТВИЯОтыскание
- 12. СОВРЕМЕННОЕ ОПРЕДЕЛЕНИЕ ЛОГАРИФМА ПОЯВИЛОСЬ У ЛЕОНАРДА ЭЙЛЕРА
- 13. ОПРЕДЕЛЕНИЕЛогарифмом положительного числа в по основанию а,
- 14. Вспомните уравнение из первого слайда:Мы говорили, что нахождение b – логарифмирование. Математики договорились записывать это так:
- 15. НАПРИМЕР:так кактак кактак кактак как
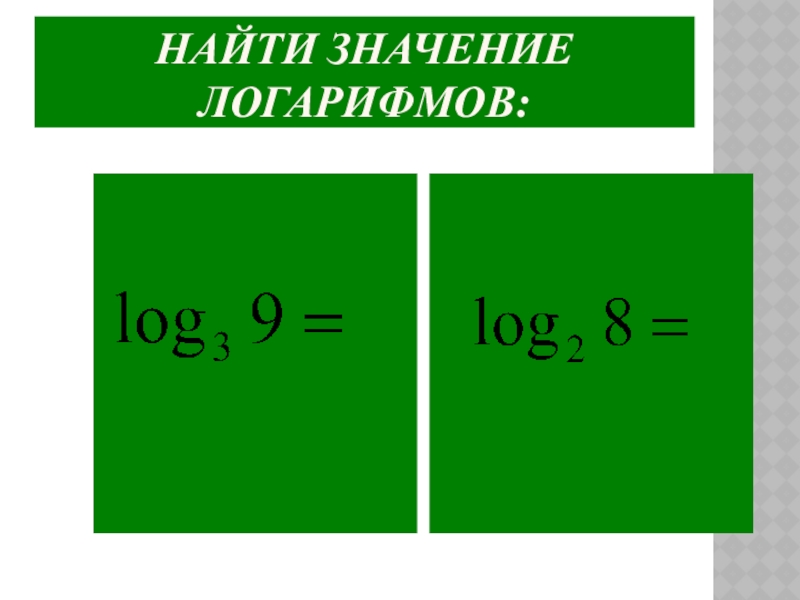
- 16. НАЙТИ ЗНАЧЕНИЕ ЛОГАРИФМОВ:
- 17. НАЙТИ ЗНАЧЕНИЕ ЛОГАРИФМОВ:
- 18. Не имеет смыслаНАЙТИ ЗНАЧЕНИЕ ЛОГАРИФМОВ:
- 19. Определение логарифма можно записать так:a log a
- 20. Log 2 16;
- 21. Сравните со своими ответами !Log 2 16;
- 22. Домашнее задание.Если со всеми предложенными заданиями Вы
- 23. СПАСИБО ЗА УРОК!
ЦЕЛИ УРОКАпознакомиться с понятием «логарифма числа», изучить основное логарифмическое тождество;научиться сравнивать, анализировать, «открывать» блок новых знаний;познакомиться с историей возникновения логарифмов.
Слайд 2ЦЕЛИ УРОКА
познакомиться с понятием «логарифма числа», изучить основное логарифмическое тождество;
научиться сравнивать,
анализировать, «открывать» блок новых знаний;
познакомиться с историей возникновения логарифмов.
познакомиться с историей возникновения логарифмов.
Слайд 4ДЛЯ ЧЕГО БЫЛИ ПРИДУМАНЫ ЛОГАРИФМЫ ?
Как сказал французский математик П. Лаплас,
«изобретение логарифмов, сократив работу астрономов, продлило им жизнь».
Слайд 5ДЛЯ ЧЕГО БЫЛИ ПРИДУМАНЫ ЛОГАРИФМЫ ?
…Если необходимость совершать обратную операцию к
операции возведения в n-ую степень, была осознана достаточно давно, то задача нахождения показателя степени по заданному результату, т. е. задача решения уравнения стала интересной лишь в XVII веке.
Слайд 6
Джон Непер
(1550-1617)
– английский математик. Изобретатель логарифмов, составитель первой таблицы логарифмов,
облегчавшей работу вычислителей многих поколений и оказавшей большое влияние на развитие приложений математики.
Слайд 9Образовательный портал "Мой университет" - www.moi-universitet.ru Факультет реформа образования - www.edu-reforma.ru
0
3
8
3
y=
3
1
2
y= 8
x
y
?
Слайд 11ВОЗВЕДЕНИЕ В СТЕПЕНЬ ИМЕЕТ ДВА ОБРАТНЫХ ДЕЙСТВИЯ
Отыскание a – извлечение корня;
Нахождение
в – логарифмирование.
Слайд 12СОВРЕМЕННОЕ ОПРЕДЕЛЕНИЕ ЛОГАРИФМА ПОЯВИЛОСЬ У ЛЕОНАРДА ЭЙЛЕРА В СЕРЕДИНЕ XVIII ВЕКА:
«…логарифмом любого числа y будет показатель степени такой, что сама степень будет равна числу y ».
Слайд 13ОПРЕДЕЛЕНИЕ
Логарифмом положительного числа в по основанию а, где а>0,a=1,называется показатель степени,
в которую нужно возвести число а ,чтобы получилось в.
Слайд 14
Вспомните уравнение из первого слайда:
Мы говорили, что нахождение b – логарифмирование.
Математики договорились записывать это так:
Слайд 19Определение логарифма можно записать так:
a log a b = b
Это равенство
справедливо при b>0, а>0, а≠1. Его обычно называют основным логарифмическим тождеством.
Например:
2 log 2 6 = 6; 3 – 2 log3 5 = (3 log 3 5 ) – 2 = 5 – 2 = 1/25.
Вычислите:
3 log 3 18; 3 5log 3 2;
10 log 10 2; (1/4) log(1/4) 6;
8 log 2 5; 9 log 3 12.
Слайд 20Log 2 16; log 2 64;
log 2 2;
Log 2 1 ; log 2 (1/2); log 2 (1/8);
Log 3 27; log 3 81; log 3 3;
Log 3 1; log 3 (1/9); log 3 (1/3);
Log1/2 1/32; log1/2 4; log0,5 0,125;
Log0/5 (1/2); log0,5 1; log1/2 2.
Log 2 1 ; log 2 (1/2); log 2 (1/8);
Log 3 27; log 3 81; log 3 3;
Log 3 1; log 3 (1/9); log 3 (1/3);
Log1/2 1/32; log1/2 4; log0,5 0,125;
Log0/5 (1/2); log0,5 1; log1/2 2.
Вычислить:
Слайд 21Сравните со своими ответами !
Log 2 16;
log 2 64; log 2 2;
Log 2 1 ; log 2 (1/2); log 2 (1/8);
Log 3 27; log 3 81; log 3 3;
Log 3 1; log 3 (1/9); log 3 (1/3);
Log1/2 1/32; log1/2 4; log0,5 0,125;
Log0,5 (1/2); log0,5 1; log1/2 2.
Log 2 1 ; log 2 (1/2); log 2 (1/8);
Log 3 27; log 3 81; log 3 3;
Log 3 1; log 3 (1/9); log 3 (1/3);
Log1/2 1/32; log1/2 4; log0,5 0,125;
Log0,5 (1/2); log0,5 1; log1/2 2.
Таблица ответов:
Слайд 22Домашнее задание.
Если со всеми предложенными заданиями Вы справились без ошибок, то
Ваше домашнее задание:
п.37, № 489, № 490, № № 495(b,в), №496(b,в,г).
п.37, № 489, № 490, № № 495(b,в), №496(b,в,г).
Если при выполнении предложенных заданий Вы испытывали затруднения и не смогли всё выполнить правильно, то Ваше домашнее задание:
п.37, № 476, № 483(b,в), № 488, № 495(b,в).
