Подготовила: преподаватель
физико-математических дисциплин
Патлаева Е.А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Параллелепипед
Содержание
- 1. Презентация по математике Параллелепипед
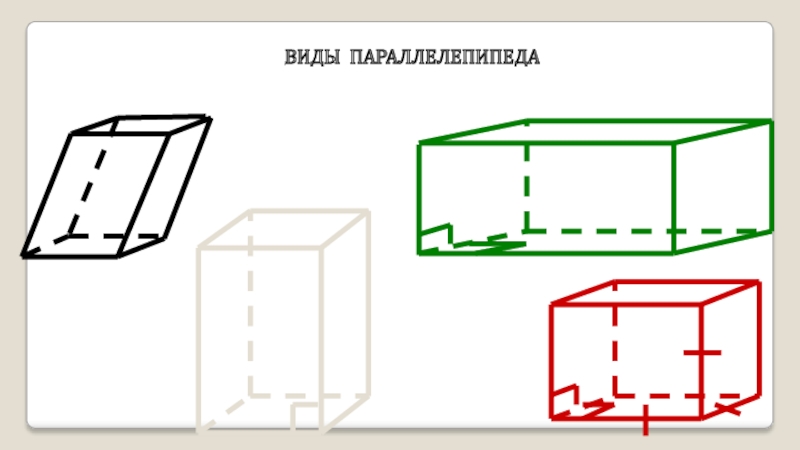
- 2. ВИДЫ ПАРАЛЛЕЛЕПИПЕДА
- 3. ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕДПараллелепипед, у которого боковые стороны перпендику-лярны основанию, называется прямым.
- 4. ПРЯМОУГОЛЬНЫЙ
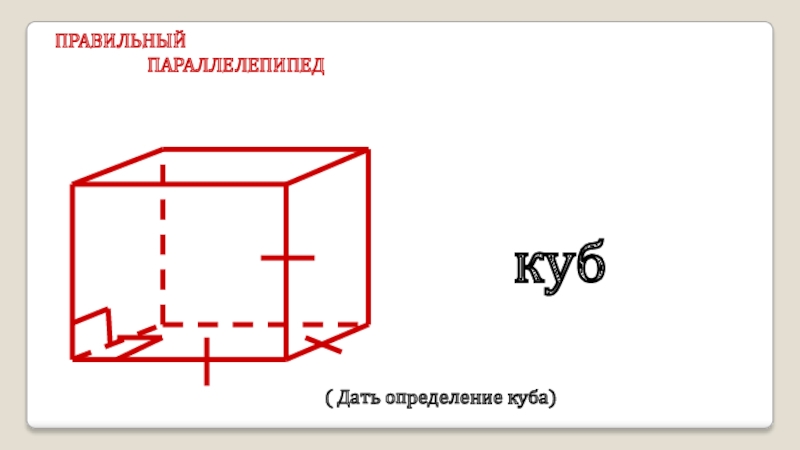
- 5. ПРАВИЛЬНЫЙ
- 6. В прямоугольном параллелепипеде все шесть
- 7. Доказать:AC1 2=AB2+AD2+AA12Доказательство:1. ABD –прямоугольныйПо т. ПифагораDB2=AB2+AD22.
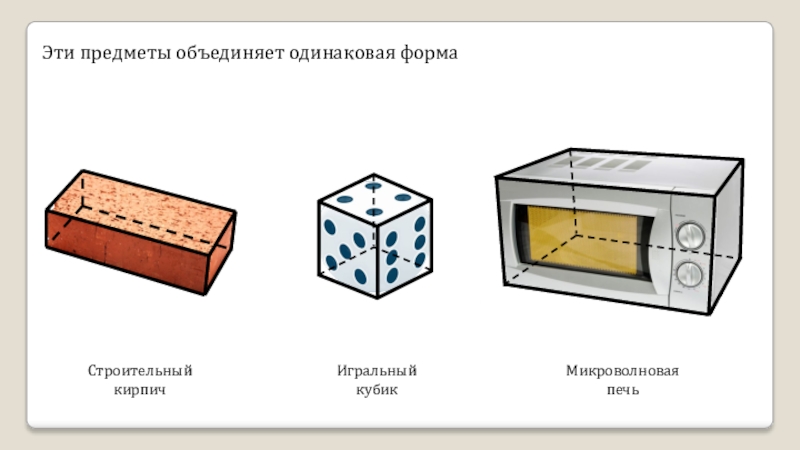
- 8. Строительный кирпичИгральный кубикМикроволновая печьРассмотрим эти предметы
- 9. Строительный кирпичИгральный кубикМикроволновая печьЭти предметы объединяет одинаковая форма
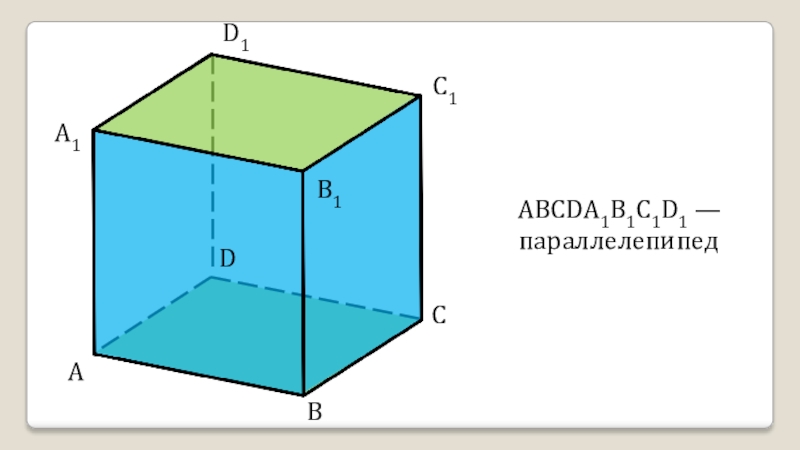
- 10. ADCBA1D1C1B1АВСDА1В1С1D1 — параллелепипед
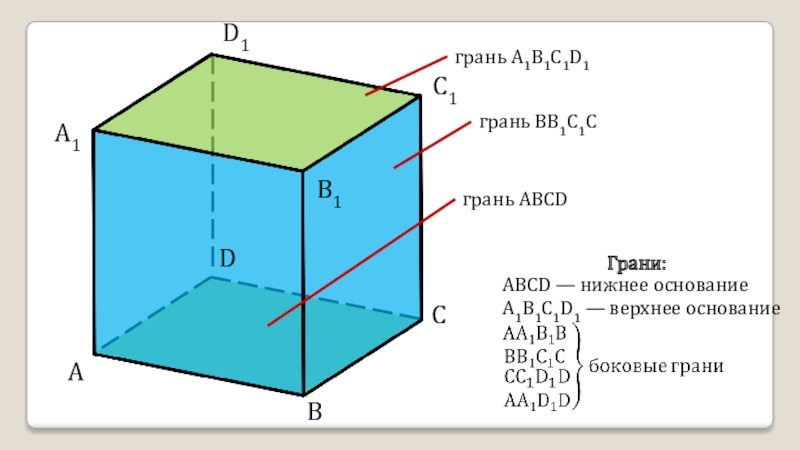
- 11. ADCBA1D1C1B1грань A1B1C1D1грань BB1C1Cгрань ABCDABCD — нижнее основаниеA1B1C1D1 — верхнее основание Грани:
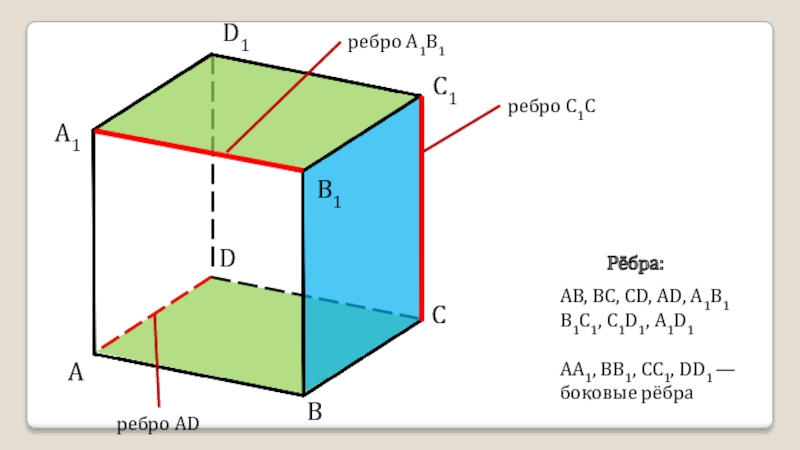
- 12. ADCBA1D1C1B1ребро A1B1ребро C1Cребро ADАВ, ВС, CD, AD,
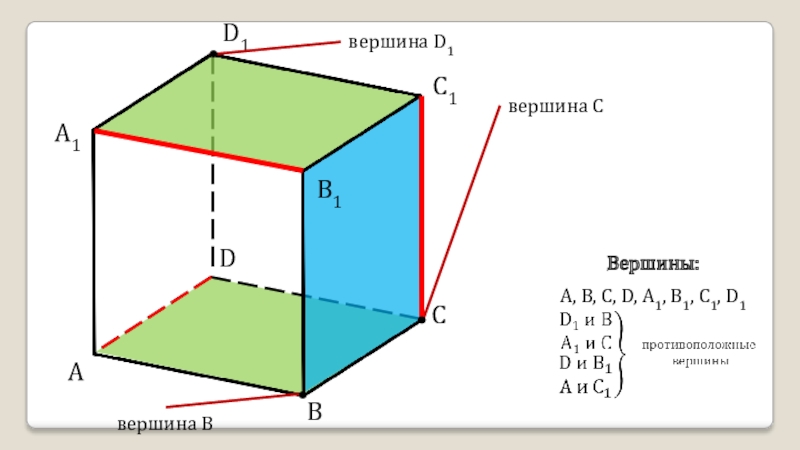
- 13. ADCBA1D1C1B1вершина D1вершина Свершина BА, В, С, D, А1, В1, С1, D1Вершины:
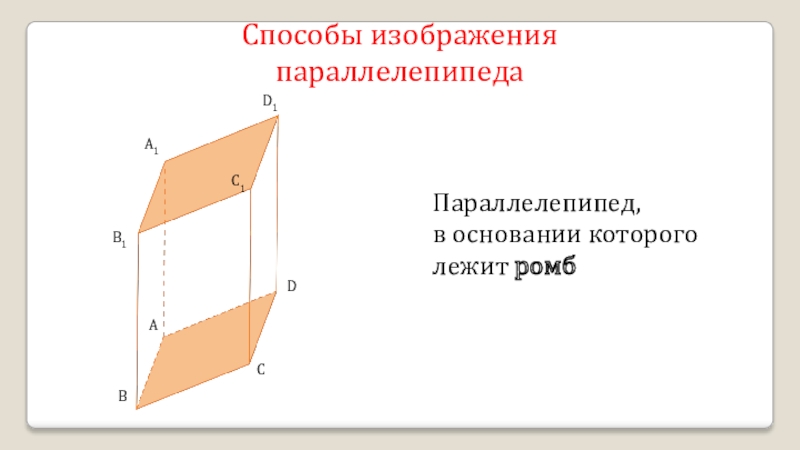
- 14. Способы изображения параллелепипедаADCBB1A1D1C1Параллелепипед, в основании которого лежит ромб
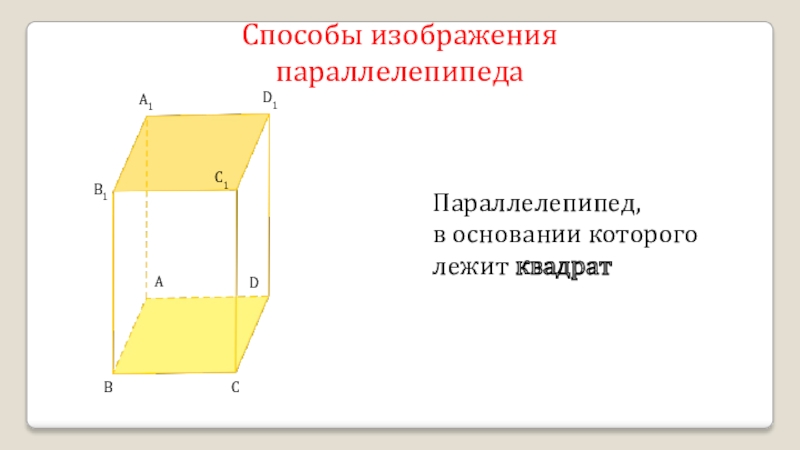
- 15. A1B1C1BCADD1Параллелепипед, в основании которого лежит квадратСпособы изображения параллелепипеда
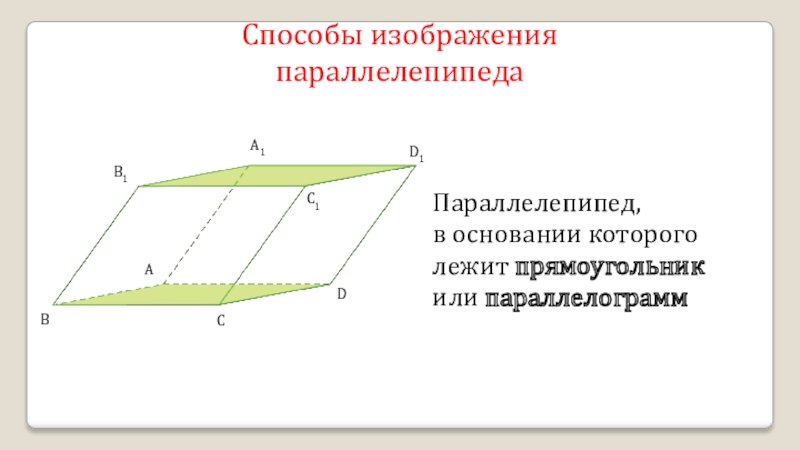
- 16. A1D1B1C1ADCBПараллелепипед, в основании которого лежит прямоугольник или параллелограммСпособы изображения параллелепипеда
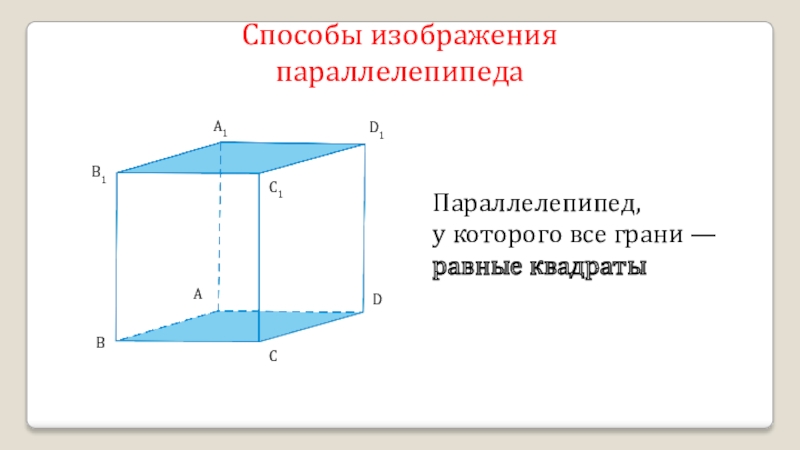
- 17. A1B1C1D1ADCBСпособы изображения параллелепипедаПараллелепипед, у которого все грани — равные квадраты
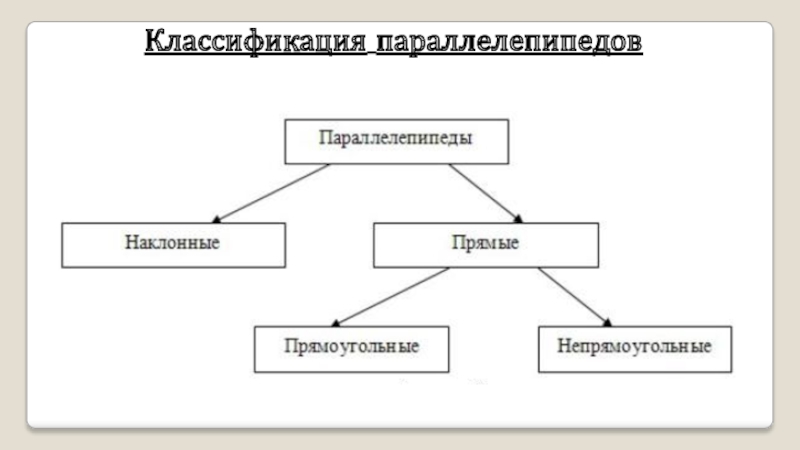
- 18. Классификация параллелепипедов
- 19. Свойство 1Противоположные грани параллелепипеда параллельны и равныДано:
- 20. ОпределениеДиагональ параллелепипеда — это отрезок, соединяющий противоположные вершиныADCBA1D1C1B1В1D, BD1, А1С — диагонали параллелепипеда
- 21. Свойство 2Диагонали параллелепипеда пересекаются в одной точке
- 22. Задача 1Дано: АВСDА1В1С1D1 — параллелепипедДоказать: ALMDNB1C1P —
ВИДЫ ПАРАЛЛЕЛЕПИПЕДА
Слайд 1П А Р А Л Л Е Л Е П И
П Е Д
Слайд 3ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД
Параллелепипед,
у которого боковые
стороны перпендику-
лярны основанию,
называется прямым.
Слайд 4ПРЯМОУГОЛЬНЫЙ
ПАРАЛЛЕЛЕПИПЕД
Параллелепипед называется прямо-
угольным, если его боковые рёбра пер- пендикулярны к основанию, а основа- ния являются прямоугольниками.
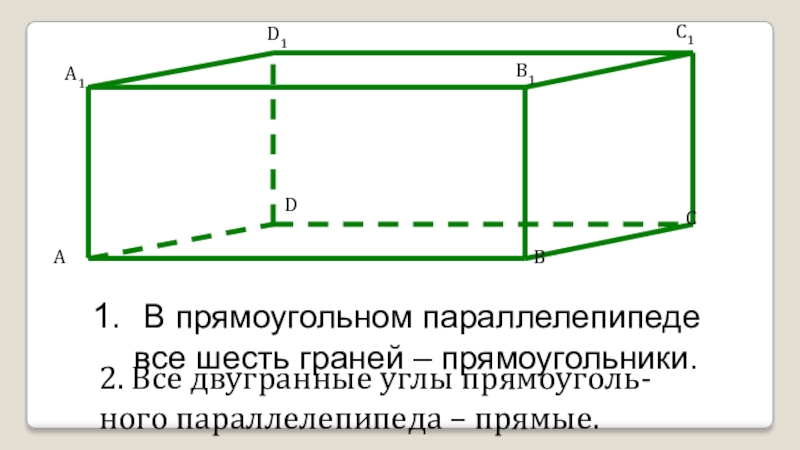
Слайд 6 В прямоугольном параллелепипеде
все шесть граней – прямоугольники.
2.
Все двугранные углы прямоуголь- ного параллелепипеда – прямые.
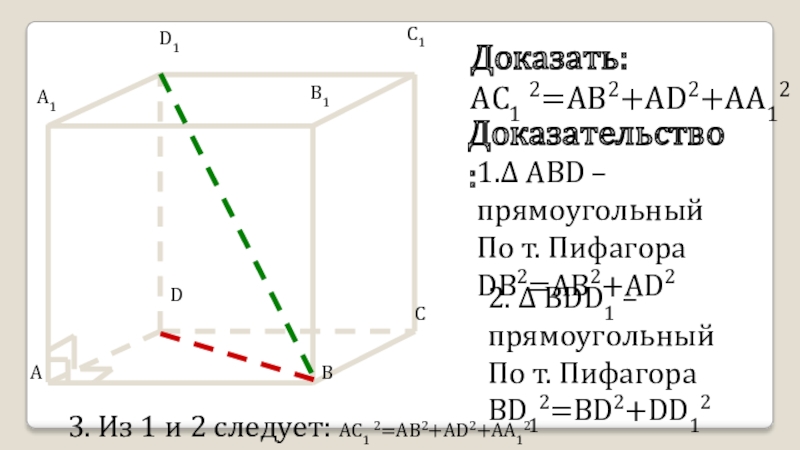
Слайд 7Доказать:
AC1 2=AB2+AD2+AA12
Доказательство:
1. ABD –прямоугольный
По т. Пифагора
DB2=AB2+AD2
2. BDD1 –
прямоугольный
По
т. Пифагора
BD12=BD2+DD12
BD12=BD2+DD12
3. Из 1 и 2 следует: AC1 2=AB2+AD2+AA12
Слайд 11A
D
C
B
A1
D1
C1
B1
грань A1B1C1D1
грань BB1C1C
грань ABCD
ABCD — нижнее основание
A1B1C1D1 — верхнее основание
Грани:
Слайд 12A
D
C
B
A1
D1
C1
B1
ребро A1B1
ребро C1C
ребро AD
АВ, ВС, CD, AD, А1В1 В1С1, C1D1, A1D1
АА1, ВВ1, СС1, DD1 — боковые рёбра
Рёбра:
Слайд 14Способы изображения параллелепипеда
A
D
C
B
B1
A1
D1
C1
Параллелепипед,
в основании которого лежит ромб
Слайд 15A1
B1
C1
B
C
A
D
D1
Параллелепипед,
в основании которого лежит квадрат
Способы изображения параллелепипеда
Слайд 16A1
D1
B1
C1
A
D
C
B
Параллелепипед,
в основании которого лежит прямоугольник или параллелограмм
Способы изображения параллелепипеда
Слайд 17A1
B1
C1
D1
A
D
C
B
Способы изображения параллелепипеда
Параллелепипед,
у которого все грани — равные квадраты
Слайд 19Свойство 1
Противоположные грани параллелепипеда параллельны
и равны
Дано: АВСDА1В1С1D1 — параллелепипед
Доказать: свойство
1
Доказательство:
1) АВСD — параллелограмм ⇒ BC ∥ AD
2) АВВ1А1 — параллелограмм ⇒ ВВ1 ∥ AA1
4) ВС = АD, ВВ1 = АА1
5) ∠В1ВС = ∠А1АD
B
A
D
C
B1
C1
D1
A1
Свойство доказано
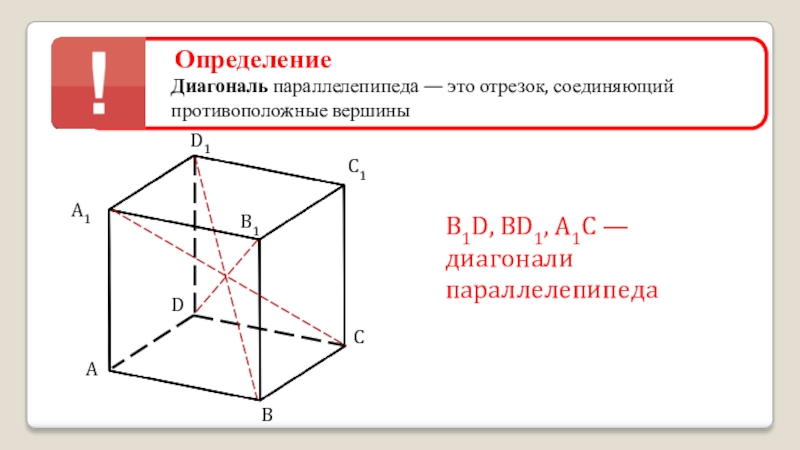
Слайд 20Определение
Диагональ параллелепипеда — это отрезок, соединяющий противоположные вершины
A
D
C
B
A1
D1
C1
B1
В1D, BD1, А1С —
диагонали параллелепипеда
Слайд 21Свойство 2
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся
пополам
Дано: АВСDА1В1С1D1 — параллелепипед
Доказать: свойство 2
Доказательство:
1) ВB1 = AA1, ВB1 ∥ AA1
АА1 = DD1, АА1 ∥ DD1
4) BC1D1A — параллелограмм ⇒
2) ВВ1 = АА1, АА1 = DD1 ⇒ ВВ1 = DD1
Свойство доказано
A
D
C
B
A1
C1
B1
D1
В1D, BD1 — диагонали ВВ1D1D
ВВ1 ∥ АА1, АА1 ∥ DD1 ⇒ ВВ1 ∥ DD1
⇒ BB1D1D — параллелограмм ⇒
⇒ В1D ∩ BD1 = О,
В1О = ОD, BO = OD1
⇒ C1A ∩ BD1 = O,
C1O = OA, BO = OD1
O
Слайд 22Задача 1
Дано: АВСDА1В1С1D1 — параллелепипед
Доказать: ALMDNB1C1P — параллелепипед
BL = CM =
A1N = D1P
1) ВВ1А1А — параллелограмм ⇒ ВВ1 = АА1, ВВ1 ∥ АА1
4) MC1PD – параллелограмм (аналогично п. 3)
5) ∠LB1N = ∠MC1P
Доказательство:
A
B
C
D
D1
B1
C1
L
M
N
P
A1
⇒ LB1 = NA, LB1 ∥ NA
⇒ LB1NA — параллелограмм
8) A1N = D1P ⇒ NA1D1P — параллелограмм ⇒ A1D1 ∥ NP ∥ AD
9) (ABB1A1) ∥ (DCC1D1) ⇒ B1C1 = LM = AD = NP
10) ANPD, NB1C1P, LB1C1M, ALMD — параллелограммы
ALMDNB1C1P — параллелепипед
Что требовалось доказать
