- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике натему Определённый интеграл
Содержание
- 1. Презентация по математике натему Определённый интеграл
- 2. «Недостаточно только
- 3. станция ТЕОРЕТИЧЕСКАЯ
- 4. 1. Что такое первообразная? Функция F(x)
- 5. 3. Что такое интегрирование? Отыскание первообразной
- 6. 5. Что такое определённый интеграл? Приращение
- 7. ВХОДНОЙ ТЕСТ
- 8. Слайд 8
- 9. Слайд 9
- 10. станция ВЫЧИСЛИТЕЛЬНАЯ
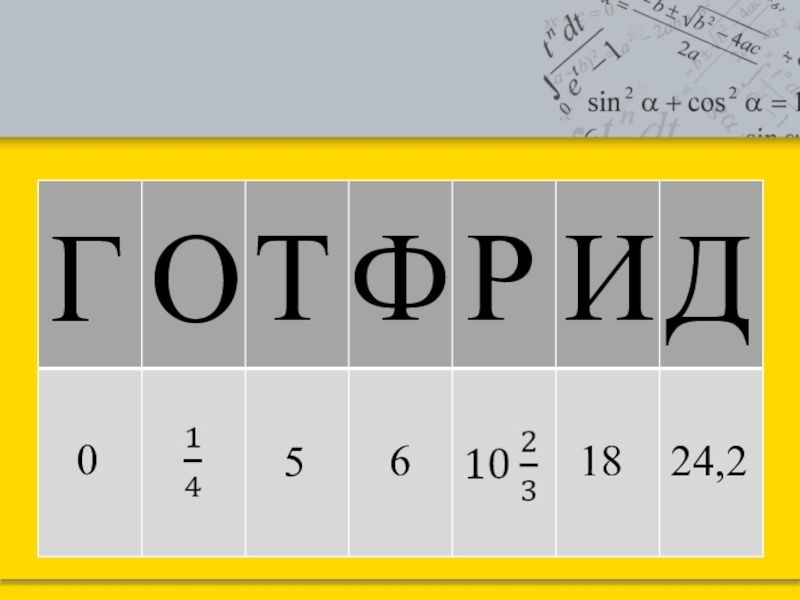
- 11. ГОТФРИД0561824,2
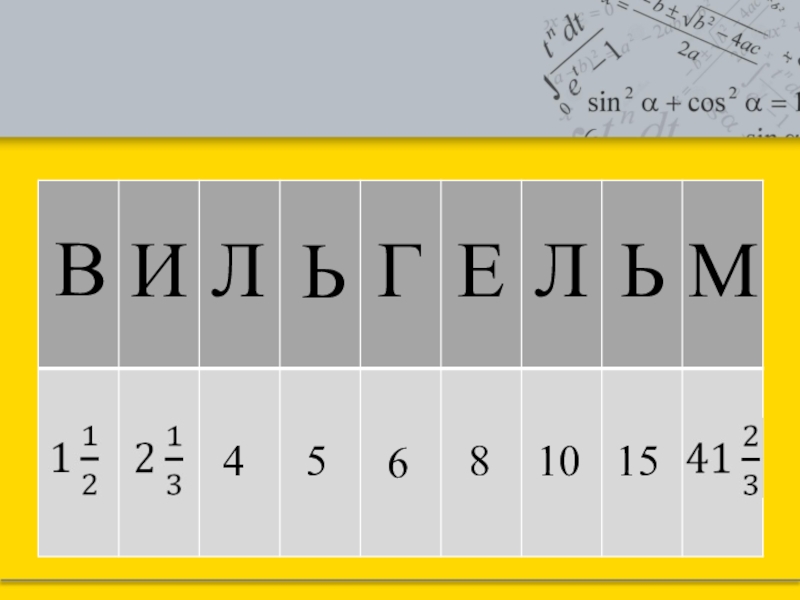
- 12. ИЛЬГЕЛЬМВ46810155
- 13. ЛЕЙБНИЦ02812,520
- 14. Лейбниц ввёл
- 15. Слайд 15
- 16. станция ИННОВАЦИОННАЯ
- 17. Слайд 17
- 18. станция ИССЛЕДОВАТЕЛЬСКАЯ
- 19. Нахождение пути, пройденного телом, при прямолинейном движении
- 20. Ʋ f (t)
- 21. Тело движется со скоростью V(t)=t+2м/с.Найти путь, который
- 22. Вычисление работы, затраченной на растяжение и сжатие пружины
- 23. [a; b]Af(x)F = kx
- 24. Определи, какую работу надо затратить на сжатие
- 25. Объём выпускаемой продукции
- 26. z = f (t)Q[0; T]
- 27. Найти объём произведённой продукции за время t=6
- 28. Задача о «каше» водакрупа
- 29. На рисунке А изображена стоящая кастрюля. На
- 30. Через точку Х оси Ох строим
- 31. станция ИТОГОВАЯ
- 32. ДОМАШНЕЕ задание
- 33. РЕФЛЕКСИЯ Мне понравилось Я убедился Я научился Я понял Я узнал Мне было интересно
«Недостаточно только получать знания, надо их систематизировать и найти им достойное приложение». И.
Слайд 2 «Недостаточно только получать знания, надо
их систематизировать
и найти им достойное
приложение».
И. Гёте
Слайд 41. Что такое первообразная?
Функция F(x) называется первообразной для функции f(x),
если F’(x)=f(x)
2. Что называется неопределённым интегралом?
Совокупность первообразных F(x)+С для функции f(x) называется неопределённым интегралом и обозначается:
2. Что называется неопределённым интегралом?
Совокупность первообразных F(x)+С для функции f(x) называется неопределённым интегралом и обозначается:
Слайд 53. Что такое интегрирование?
Отыскание первообразной функции по заданной её производной.
4.
Каким действие можно проверить интегрирование?
Дифференцированием.
Дифференцированием.
Слайд 65. Что такое определённый интеграл?
Приращение F(b)-F(a) первообразных функций при изменении
аргумента от a до b, называется определённым интегралом.
6. Какие свойства используются при вычислении интеграла?
6. Какие свойства используются при вычислении интеграла?
Слайд 14
Лейбниц ввёл современное обозначение неопределённого интеграла. Он
адаптировал интегральный символ, обра-зованный из буквы S – сокра-щения лат. слова «summa». Современное обозначение интеграла с ограничениями над и под знаком интеграла, были впервые использованы Ж. Фурье в 1819-1820 годах.
Слайд 21Тело движется со скоростью V(t)=t+2м/с.
Найти путь, который пройдёт тело за 2
секунды
после начала движения.
после начала движения.
Решение
= 0 – начало движения,
= 2 сек. – время завершения движения.
Значит путь, пройденный телом за 2 сек. после начала движения найдём по формуле:
![[a; b]Af(x)F = kx](/img/thumbs/d09fff61b9fc23431adb6ac94a075ae4-800x.jpg "Презентация по математике натему Определённый интеграл [a; b]Af(x)F = kx")
Слайд 24Определи, какую работу надо затратить на
сжатие пружины на 2 см,
если известно, что
сила в 4Н сжимает её на 1 см.
сила в 4Н сжимает её на 1 см.
Решение
![z = f (t)Q[0; T]](/img/thumbs/06da450935b0746a9184366f8751f0a8-800x.jpg "Презентация по математике натему Определённый интеграл z = f (t)Q[0; T]")
Слайд 27Найти объём произведённой продукции за
время t=6 час, если производительность труда
задана функцией f(t) = - +10t (ед/час)
Решение
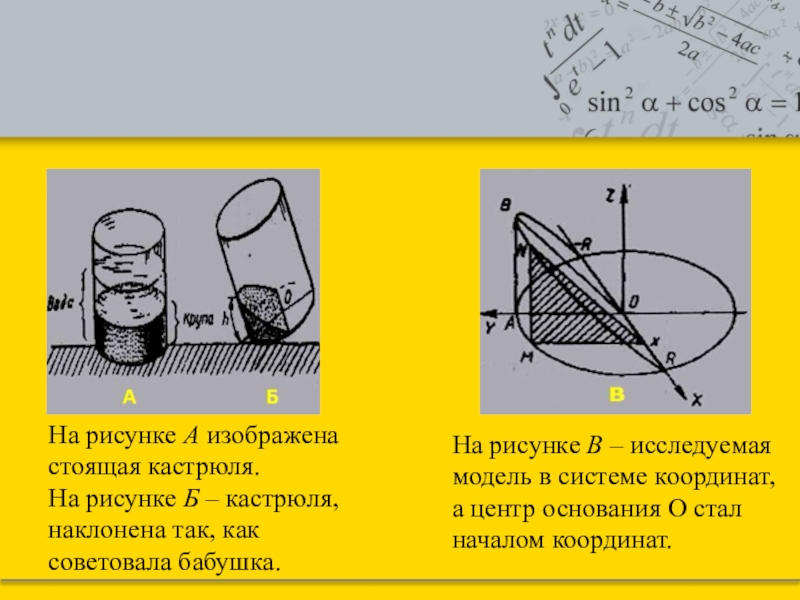
Слайд 29На рисунке А изображена стоящая кастрюля.
На рисунке Б – кастрюля,
наклонена так, как советовала бабушка.
На рисунке В – исследуемая модель в системе координат, а центр основания О стал началом координат.
Слайд 30
Через точку Х оси Ох строим сечение тела (т.е. горки их
крупы внутри кастрюли) плоскостью, перпендикуляр-ной оси Ох и параллельной оси Оу. Рассматривая подобие треугольников MNХ и АВО приходим к выводу, что
Т.е эта величина не зависит от
размеров цилиндра (кастрюли)
Т.е эта величина не зависит от
размеров цилиндра (кастрюли)
