- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на темуАксиома параллельности прямых
Содержание
- 1. Презентация по математике на темуАксиома параллельности прямых
- 2. aMcbb1
- 3. НИКОЛАЙ ИВАНОВИЧ ЛОБАЧЕВСКИЙ(1792-1856)
- 4. АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ:ЧЕРЕЗ ТОЧКУ, НЕ ЛЕЖАЩУЮ НА ДАННОЙ ПРЯМОЙ, ПРОХОДИТ ТОЛЬКО ОДНА ПРЯМАЯ, ПАРАЛЛЕЛЬНАЯ ДАННОЙ
- 5. УТВЕРЖДЕНИЯ, КОТОРЫЕ ВЫВОДЯТСЯ НЕПОСРЕДСТВЕННО ИЗ АКСИОМ ИЛИ ТЕОРЕМ НАЗЫВАЮТСЯ СЛЕДСТВИЯМИ
- 6. ТЕОРЕМА:В РАВНОБЕДРЕННОМ ТРЕУГОЛЬНИКЕ БИССЕКТРИСА, ПРОВЕДЕННАЯ К ОСНОВАНИЮ,
- 7. СЛЕДСТВИЯ ИЗ АКСИОМЫ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ:1. ЕСЛИ ПРЯМАЯ
- 8. СЛЕДСТВИЯ ИЗ АКСИОМЫ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ:2. ЕСЛИ ДВЕ ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ ТРЕТЬЕЙ ПРЯМОЙ, ТО ОНИ ПАРАЛЛЕЛЬНЫabc
aMcbb1
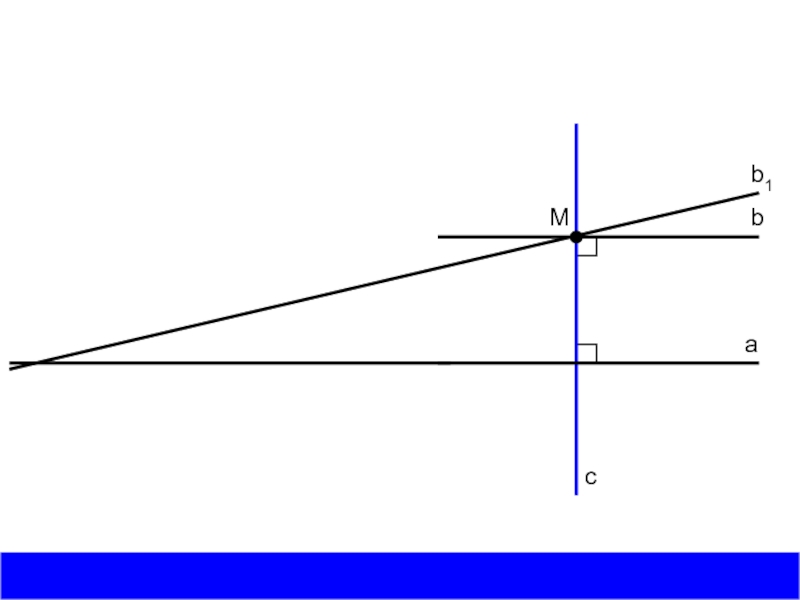
Слайд 4АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ:
ЧЕРЕЗ ТОЧКУ, НЕ ЛЕЖАЩУЮ НА ДАННОЙ ПРЯМОЙ, ПРОХОДИТ ТОЛЬКО
ОДНА ПРЯМАЯ, ПАРАЛЛЕЛЬНАЯ ДАННОЙ
Слайд 6
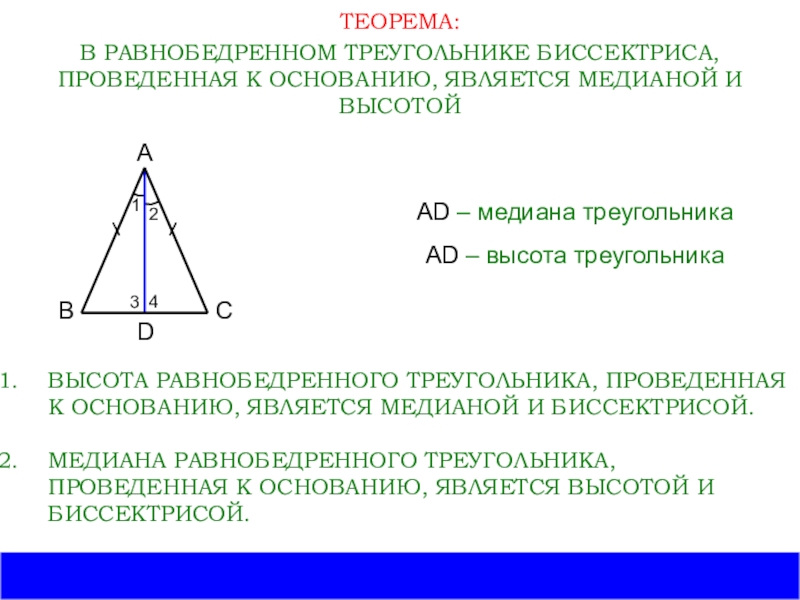
ТЕОРЕМА:
В РАВНОБЕДРЕННОМ ТРЕУГОЛЬНИКЕ БИССЕКТРИСА, ПРОВЕДЕННАЯ К ОСНОВАНИЮ, ЯВЛЯЕТСЯ МЕДИАНОЙ И ВЫСОТОЙ
А
В
С
1
2
D
AD
– медиана треугольника
3
4
AD – высота треугольника
ВЫСОТА РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА, ПРОВЕДЕННАЯ К ОСНОВАНИЮ, ЯВЛЯЕТСЯ МЕДИАНОЙ И БИССЕКТРИСОЙ.
МЕДИАНА РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА, ПРОВЕДЕННАЯ К ОСНОВАНИЮ, ЯВЛЯЕТСЯ ВЫСОТОЙ И БИССЕКТРИСОЙ.
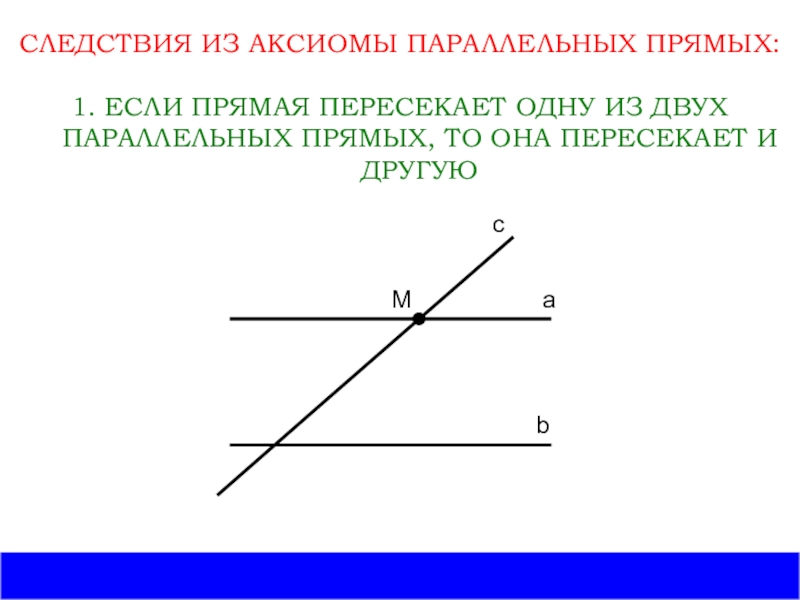
Слайд 7СЛЕДСТВИЯ ИЗ АКСИОМЫ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ:
1. ЕСЛИ ПРЯМАЯ ПЕРЕСЕКАЕТ ОДНУ ИЗ ДВУХ
ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ, ТО ОНА ПЕРЕСЕКАЕТ И ДРУГУЮ
b
M
a
c
Слайд 8СЛЕДСТВИЯ ИЗ АКСИОМЫ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ:
2. ЕСЛИ ДВЕ ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ ТРЕТЬЕЙ ПРЯМОЙ,
ТО ОНИ ПАРАЛЛЕЛЬНЫ
a
b
c