- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Занимательные задачи
Содержание
- 1. Презентация по математике на тему Занимательные задачи
- 2. Второе февраля. Классная работа.
- 3. «Тупиковые ситуации» лишь для того и существуют, чтобы стимулировать наше мышление !
- 4. Проверка домашней работы
- 5. З1.Число, которое не является не
- 6. Второе февраля. Классная работа. Занимательные задачи.
- 7. Его величество граф Слово «ГРАФ» в
- 8. Одним росчеркомЕсли все вершины графа четные, то
- 9. Одним росчеркомГраф, имеющий всего две нечетные вершины,
- 10. История возникновения графовОсновы теории графов как математической
- 11. Одним росчеркомГраф, который можно нарисовать, не отрывая
- 12. (Д/з)34242324Стр. 156
- 13. Вычисли2³ =8354 – 198 =1563²· 2² =36S
- 14. Стр. 160
- 15. Вычисли49·79 + 21·49=4 90054·1972 – 54·972=54 00013·а
- 16. 100! = 1·2·3· …·98·99·100100! = · 10099!?Д/зСтр. 160
- 17. Задачи - шуткиИнформация Гарницкой Марины
- 18. Математический папирус Ахмеса также известен как папирус
- 19. Папирус Ахмеса Математический папирус Ахмеса — древнеегипетское
- 20. Был организатором и руководителем монастырской школы в
- 21. Задача
- 22. Домашняя работа1. Повторить п. 3.1 – 3.62.
- 23. Спасибо за урокУдачи
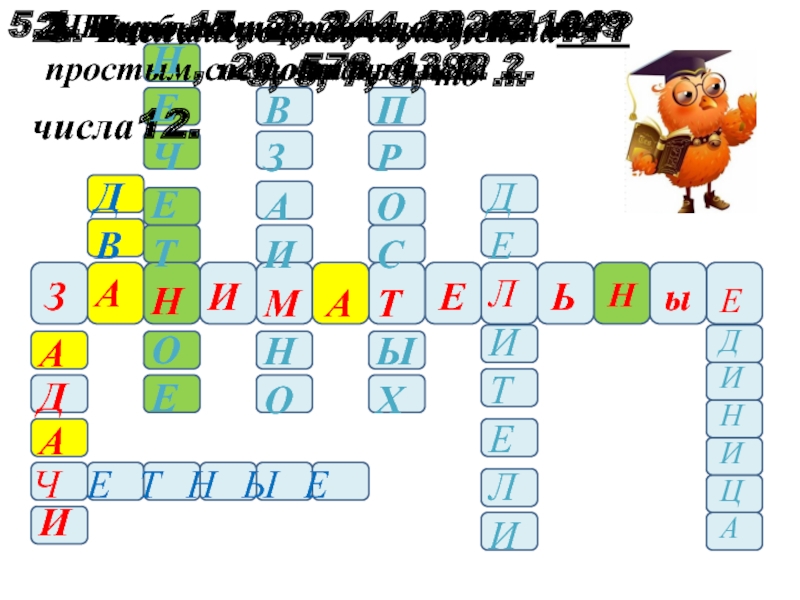
Слайд 5З
1.Число, которое не является не простым, не составным ?
Е
Д
И
Н
И
Ц
А
2.
числа12.
Д
Е
Л
И
Т
Е
Л
И
3. Если число оканчивается на
3, 5, 7, 9, то …
Н
Е
Ч
Е
Т
Н
О
Е
Н
4. Пары 15 и 2, 24 и 19, 64 и 49
состоят из чисел …
В
З
А
И
М
Н
О
П
Р
О
С
Т
Ы
Х
5. Что объединяет числа 124, 16,
20, 578, 1392 ?
Ч Е Т Н Ы Е
Д
В
А
А
А
И
А
Е
Ь
ы
Д
И
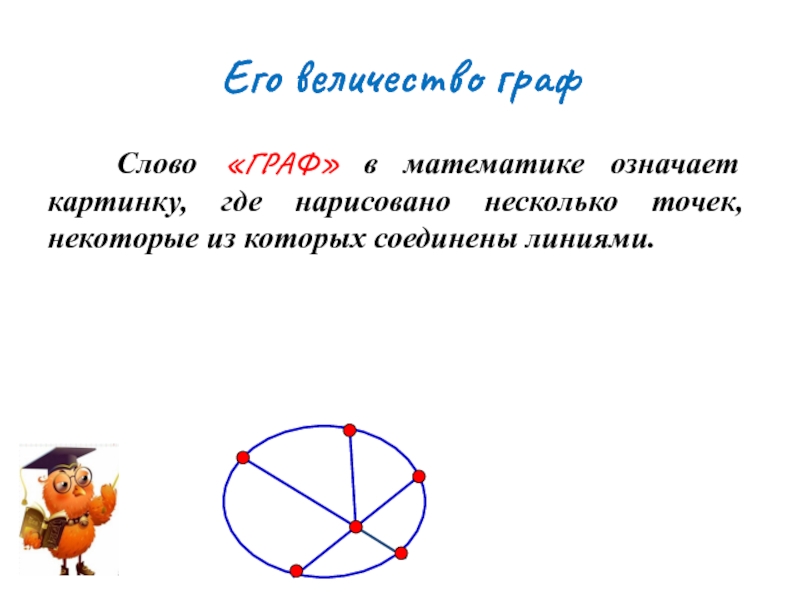
Слайд 7Его величество граф
Слово «ГРАФ» в математике означает картинку, где
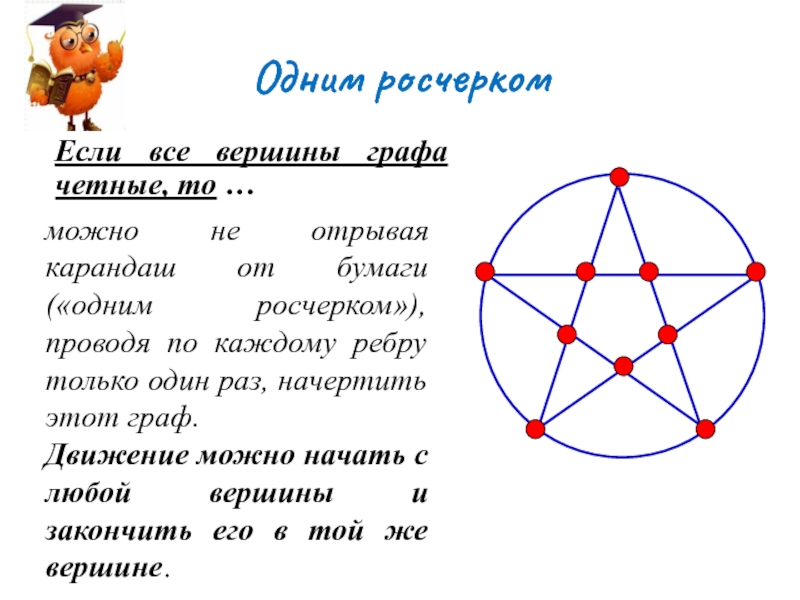
Слайд 8Одним росчерком
Если все вершины графа четные, то …
можно не отрывая карандаш
Движение можно начать с любой вершины и закончить его в той же вершине.
Слайд 9Одним росчерком
Граф, имеющий всего две нечетные вершины,
можно начертить, не отрывая
Слайд 10История возникновения графов
Основы теории графов как математической науки заложил в 1736
(Задача № 712)
Слайд 11Одним росчерком
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется
Решая задачу О кенигсбергских мостах, Эйлер сформулировал свойства графа:
Невозможно начертить граф с нечетным числом нечетных вершин.
Слайд 13Вычисли
2³ =
8
354 – 198 =
156
3²· 2² =
36
S куба = 100 м²
а = 10 м
V куба = 27 м³
а = 3 м
2! = ?
№ 719
стр. 160
Слайд 15Вычисли
49·79 + 21·49=
4 900
54·1972 – 54·972=
54 000
13·а + 9·а =
22·а
14·m –m
?
m· (14 – 1)= 13· m
Слайд 18Математический папирус Ахмеса также известен как папирус Ринда – древнеегипетское учебное
Историческая страничка
Слайд 19Папирус Ахмеса
Математический папирус Ахмеса — древнеегипетское учебное руководство по арифметике
Папирус Ахмеса был обнаружен в 1858 шотландским египтологом Генри Риндом и часто называется папирусом Райнда по имени его первого владельца. В 1870 папирус был расшифрован, переведён и издан. Ныне большая часть рукописи находится в Британском музеев Лондоне, а вторая часть — в Нью - Йорке.
Слайд 20Был организатором и руководителем монастырской школы в Туре (Франция). Учителем в
Историческая страничка
Алкуин– английский
монах ученый.
(ок. 735 -804)
Слайд 22Домашняя работа
1. Повторить п. 3.1 – 3.6
2. Решить № 710,
№
3. Дополнительное задание
№ 727 (а), задача Эйлера
№ 712 (задания на выбор)