вы развиваетесь.
Шахматы взаимосвязаны с математикой.
ТЕМА ЗАНЯТИЯ:
«Взаимосвязь шахмат и математики.
Секретный ход шахматной пешки»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Взаимосвязь математики и шахматной науки
Содержание
- 1. Презентация по математике на тему: Взаимосвязь математики и шахматной науки
- 2. Шахматная наука – гимнастика для ума, искусство
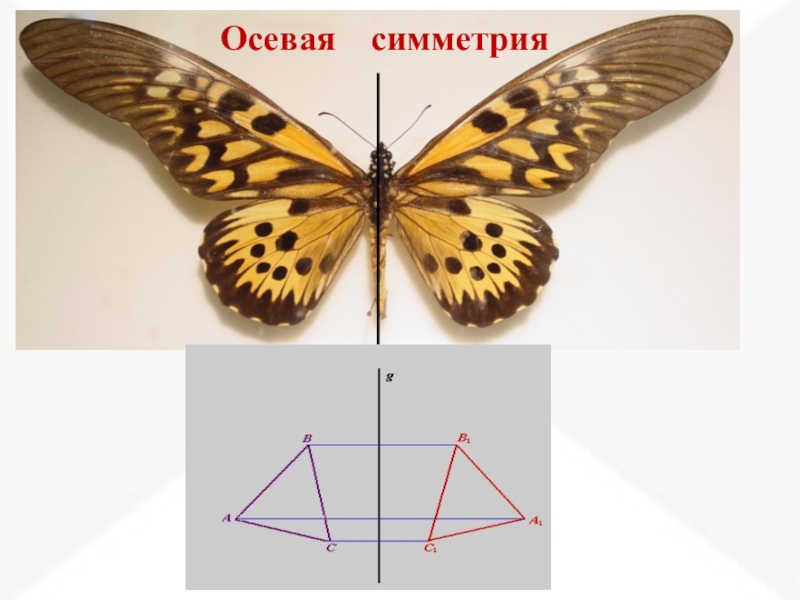
- 3. Осевая симметрия
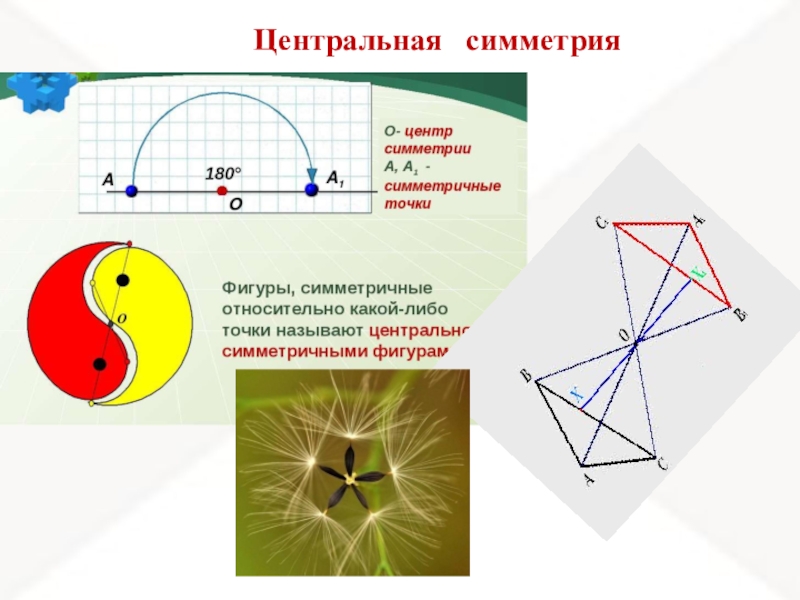
- 4. Центральная симметрия
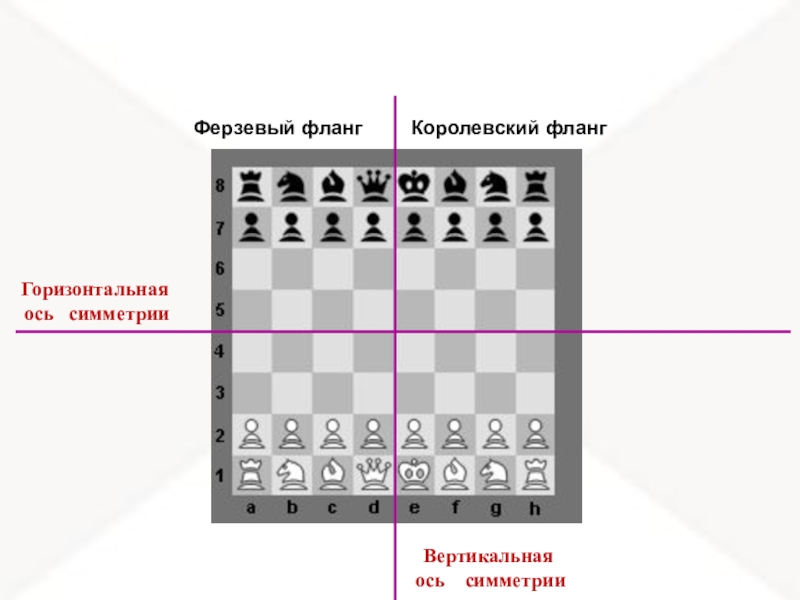
- 5. Королевский флангФерзевый флангГоризонтальная ось симметрииВертикальная ось симметрии
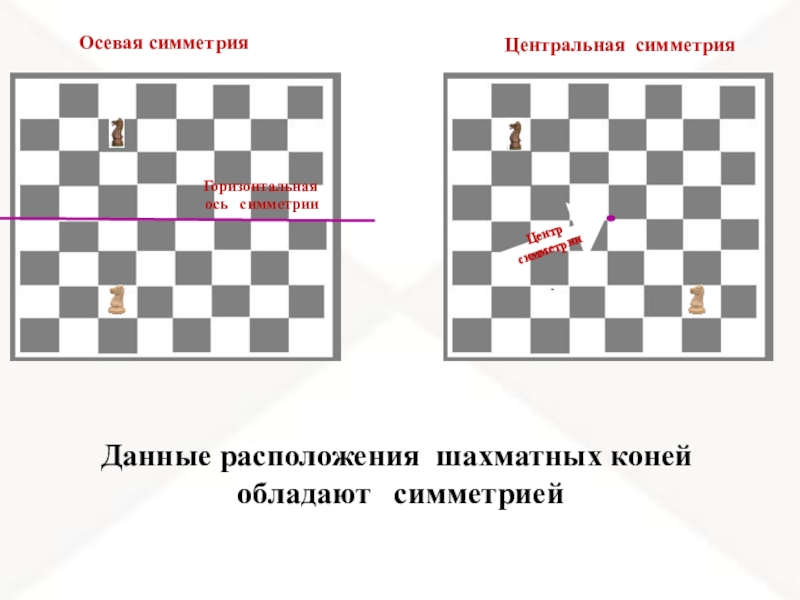
- 6. Горизонтальная ось симметрииДанные расположения шахматных коней обладают симметриейЦентр симметрииОсевая симметрияЦентральная симметрия
- 7. Чётность и нечётность Цифры 0,
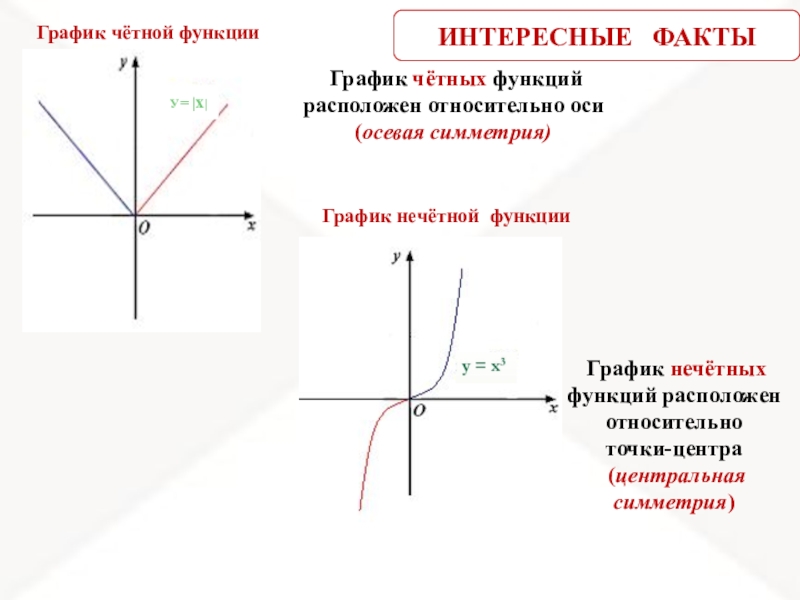
- 8. График чётных функций расположен относительно оси(осевая
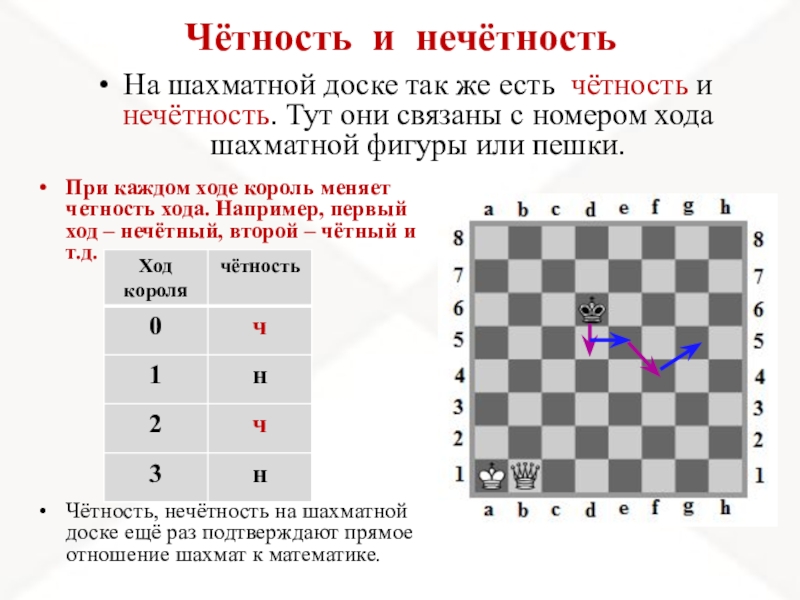
- 9. Чётность и нечётность На шахматной доске так
- 10. Задача на дом:Может ли конь пройти
- 11. Белый конь держит под боем поля (битые
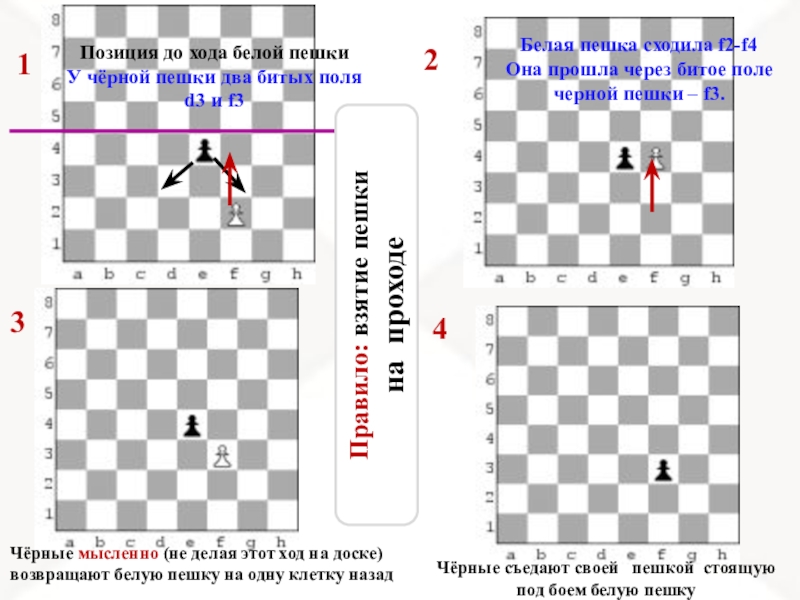
- 12. 1234Чёрные мысленно (не делая этот ход на доске) возвращают
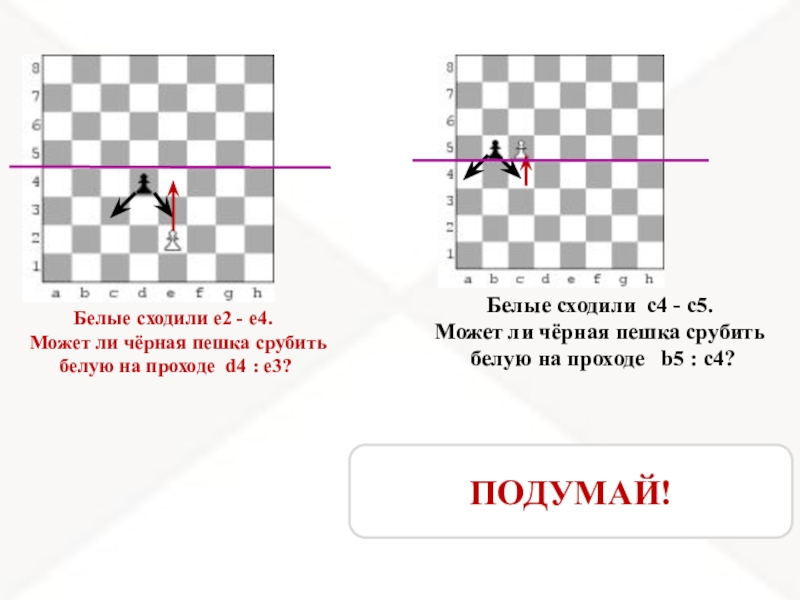
- 13. Белые сходили е2 - е4. Может
- 14. Белые сходили е2 - е4. Может
- 15. Если при своём ходе из начальной позиции
- 16. Белые:Кра2;Фс6;а3;в4Чёрные:Кра5;Фd6;Сd4;а4Белые только что сходили пешкой b2-b4 и
- 17. ИТОГ ЗАНЯТИЯ С какими терминами
- 18. Сколькими способами можно расставить на шахматной доске
Шахматная наука – гимнастика для ума, искусство мыслить. Играя в шахматы вы развиваетесь. Шахматы взаимосвязаны с математикой.ТЕМА ЗАНЯТИЯ:«Взаимосвязь шахмат и математики. Секретный ход шахматной пешки»
Слайд 6Горизонтальная
ось симметрии
Данные расположения шахматных коней
обладают симметрией
Центр симметрии
Осевая
симметрия
Центральная симметрия
Слайд 7
Чётность и нечётность
Цифры 0, 2, 4, 6, 8 называются чётными,
а цифры 1, 3, 5, 7, 9 нечётными.
Натуральные числа, которые делятся на 2, называются чётными, остальные – нечётными.
Натуральные числа, которые делятся на 2, называются чётными, остальные – нечётными.
Слайд 8
График чётных функций расположен относительно оси
(осевая симметрия)
График нечётных функций
расположен относительно
точки-центра
(центральная симметрия)
точки-центра
(центральная симметрия)
График чётной функции
График нечётной функции
У= |x|
ИНТЕРЕСНЫЕ ФАКТЫ
Слайд 9Чётность и нечётность
На шахматной доске так же есть чётность и
нечётность. Тут они связаны с номером хода шахматной фигуры или пешки.
При каждом ходе король меняет четность хода. Например, первый ход – нечётный, второй – чётный и т.д.
Чётность, нечётность на шахматной доске ещё раз подтверждают прямое отношение шахмат к математике.
Слайд 10
Задача на дом:
Может ли конь пройти с поля a8 на поле
h1, побывав по дороге на каждом из остальных полей ровно один раз?
Шахматный конь вышел на поле а8 и через несколько ходов вернулся на него. Докажите, что он сделал чётное число ходов (вспомни особенность хода коня).
Задачи на чётность и нечётность
Слайд 11Белый конь держит под боем поля (битые поля) b3 и c2,
пешка держит под боем поля (битые поля) е3 и g3.
Битое поле – поле, которое находится
под ударом какой- либо
шахматной фигуры или пешки
Слайд 121
2
3
4
Чёрные мысленно (не делая этот ход на доске)
возвращают белую пешку на одну
клетку назад
Чёрные съедают своей пешкой стоящую
под боем белую пешку
Позиция до хода белой пешки
У чёрной пешки два битых поля
d3 и f3
Белая пешка сходила f2-f4
Она прошла через битое поле черной пешки – f3.
Правило: взятие пешки
на проходе
Слайд 13Белые сходили е2 - е4.
Может ли чёрная пешка срубить
белую на проходе d4 : e3?
Белые сходили с4 - с5.
Может ли чёрная пешка срубить
белую на проходе b5 : c4?
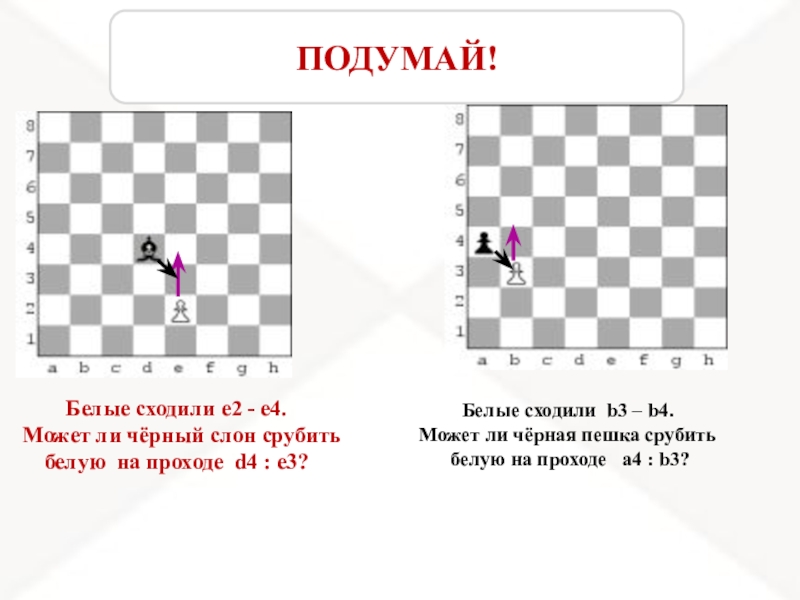
ПОДУМАЙ!
Слайд 14Белые сходили е2 - е4.
Может ли чёрный слон срубить
белую на проходе d4 : e3?
Белые сходили b3 – b4.
Может ли чёрная пешка срубить
белую на проходе a4 : b3?
ПОДУМАЙ!
Слайд 15Если при своём ходе из начальной позиции пешка (например, белая) прыгает
через битое поле неприятельской (черной) пешки, то неприятельская (черная) пешка может мысленно (не делая этого хода на доске) вернуть (белую) пешку на одну клетку назад, и съесть её как будто та (белая пешка) сделала ход лишь на одно поле.
Взятие на проходе можно делать только сразу же после хода пешки. Если вы этого не сделали, то следующим ходом эту пешку съесть на проходе нельзя!
Правило взятия на проходе действует только для пешек! Никакая другая фигура есть на проходе не может!
Взятие на проходе можно делать только сразу же после хода пешки. Если вы этого не сделали, то следующим ходом эту пешку съесть на проходе нельзя!
Правило взятия на проходе действует только для пешек! Никакая другая фигура есть на проходе не может!
Правило: взятие пешки на проходе
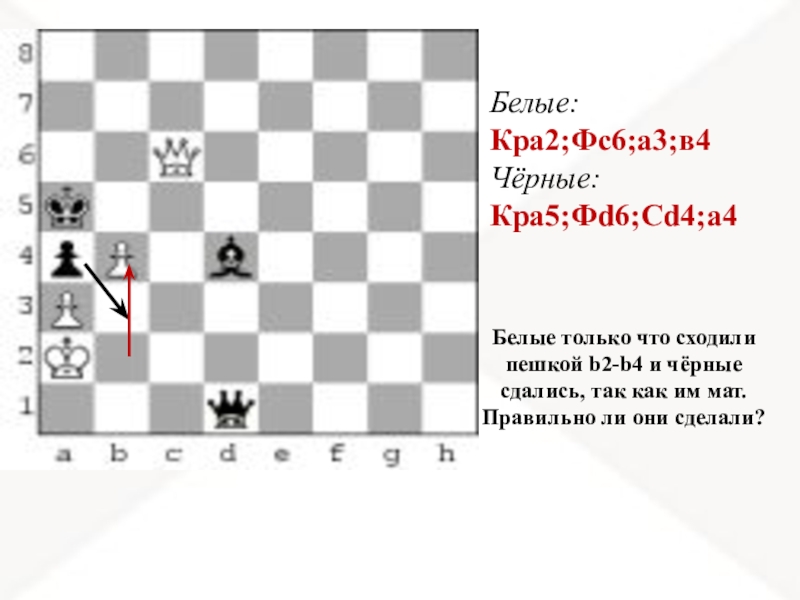
Слайд 16Белые:
Кра2;Фс6;а3;в4
Чёрные:
Кра5;Фd6;Сd4;а4
Белые только что сходили пешкой b2-b4 и чёрные сдались, так как
им мат. Правильно ли они сделали?
Слайд 17 ИТОГ ЗАНЯТИЯ С какими терминами вы сегодня познакомились? Что вы узнали на
занятии?
Шахматная ситуация: какая вы сегодня шахматная фигура?
(шкала ценности шахматных фигур соответствует усвоению полученных знаний)
Слайд 18Сколькими способами можно расставить на шахматной доске восемь ладьей так, чтобы
ни одна из них не могла побить другую.
Решение. На первую горизонталь ладью можно поставить восемью способами. После того как ладья поставлена на первую горизонталь, на второй горизонтали есть лишь семь доступных нам полей (ставить две ладьи на одну вертикаль нельзя!). На третьей горизонтали останется лишь шесть полей, на четвертой – пять полей и т.д. По комбинаторному правилу произведения получаем
8·7·6·5·4· 3·2·1 = 8! = 40320
40320 допустимых расстановок (способов)
Решение. На первую горизонталь ладью можно поставить восемью способами. После того как ладья поставлена на первую горизонталь, на второй горизонтали есть лишь семь доступных нам полей (ставить две ладьи на одну вертикаль нельзя!). На третьей горизонтали останется лишь шесть полей, на четвертой – пять полей и т.д. По комбинаторному правилу произведения получаем
8·7·6·5·4· 3·2·1 = 8! = 40320
40320 допустимых расстановок (способов)
Комбинаторная задача.
