- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Высказывание. Логические операции над высказываниями. Формализация высказываний
Содержание
- 1. Презентация по математике на тему Высказывание. Логические операции над высказываниями. Формализация высказываний
- 2. высказываниЕВысказывание - это повествовательное предложение, о котором
- 3. высказывание
- 4. высказываниЕ
- 5. высказываниЕ
- 6. В математической логике интересуются
- 7. Составное высказывание – это высказывание,
- 8. Труды и работы:Джон Венн расширил математическую логику Буля и более
- 9. Высказывание, не содержащее логические связки, называется элементарным.ЭЛЕМЕНТАРНЫЕ высказываниЯ
- 10. В алгебре высказываний над высказываниями можно производить
- 11. Это высказывание, истинное тогда и только тогда,
- 12. Конъюнкция двух высказываний А и ВА и
- 13. Дизъюнкция двух высказываний А и ВЭто высказывание
- 14. Импликация двух высказываний А и ВЭто высказывание
- 15. Эквиваленция двух высказываний А и ВЭто высказывание
- 16. Порядок выполнения логических операцийОтрицаниеКонъюнкция ДизъюнкцияИмпликацияЭквиваленцияИзменить порядок выполнения операций может расстановка скобок
- 17. Формализация высказыванийПри формализации высказываний удобно использовать следующий
- 18. Формализация высказыванийПри формализации высказываний удобно использовать следующий
- 19. Формализация высказыванийС=«Положительный ряд сходится тогда и только
- 20. Формализация высказыванийD = «Верность теорий проверяется не
высказываниЕВысказывание - это повествовательное предложение, о котором в данный момент времени можно сказать, что оно либо истинно, либо ложно (но не то и другое одновременно)
Слайд 1
ВЫСКАЗЫВАНИЕ. логические операции НАД ВЫСКАЗЫВАНИЯМИ. формализация ВЫСКАЗЫВАний.
Автор презентации: Холманова В. М.
Слайд 2высказываниЕ
Высказывание - это повествовательное предложение, о котором в данный момент времени
можно сказать, что оно либо истинно, либо ложно (но не то и другое одновременно)
Слайд 6 В математической логике интересуются главным образом не содержанием
высказывания, а его истинностным (истинное или ложное) значением.
Если высказывание истинное, то ему соответствует значение логической переменной, равное 1.
Если высказывание ложное, то ему соответствует значение логической переменной, равное 0.
Если высказывание истинное, то ему соответствует значение логической переменной, равное 1.
Если высказывание ложное, то ему соответствует значение логической переменной, равное 0.
высказываниЕ
Слайд 7 Составное высказывание – это высказывание, содержащее логические связки.
Логические связки: не, и, а, но, или, либо, если…, то, тогда и только тогда, когда, неверно, что и другие.
В = «В честь английского логика Джона Венна в Кембридже установлен мемориальный витраж, а в городе Халл построен университетский корпус»
В = «В честь английского логика Джона Венна в Кембридже установлен мемориальный витраж, а в городе Халл построен университетский корпус»
СОСТАВНЫЕ высказываниЯ
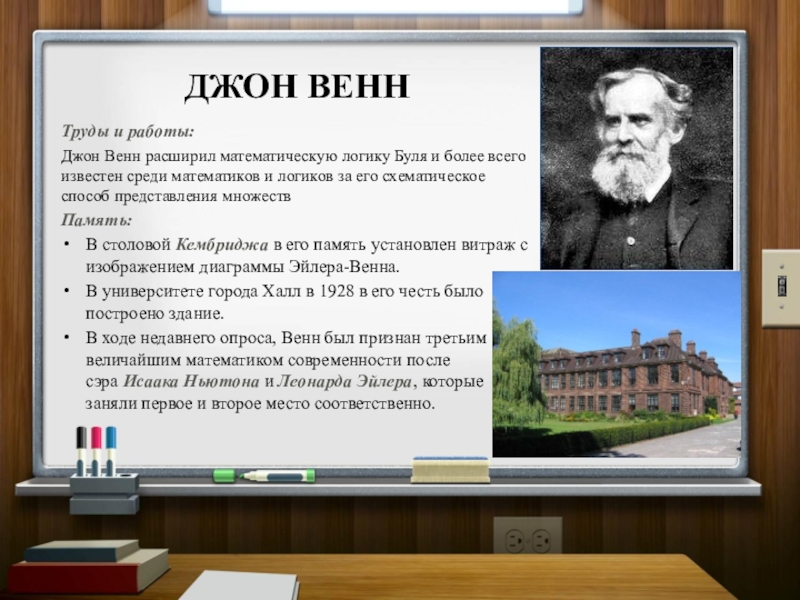
Слайд 8Труды и работы:
Джон Венн расширил математическую логику Буля и более всего известен среди математиков
и логиков за его схематическое способ представления множеств
Память:
В столовой Кембриджа в его память установлен витраж с изображением диаграммы Эйлера-Венна.
В университете города Халл в 1928 в его честь было построено здание.
В ходе недавнего опроса, Венн был признан третьим величайшим математиком современности после сэра Исаака Ньютона и Леонарда Эйлера, которые заняли первое и второе место соответственно.
Память:
В столовой Кембриджа в его память установлен витраж с изображением диаграммы Эйлера-Венна.
В университете города Халл в 1928 в его честь было построено здание.
В ходе недавнего опроса, Венн был признан третьим величайшим математиком современности после сэра Исаака Ньютона и Леонарда Эйлера, которые заняли первое и второе место соответственно.
ДЖОН ВЕНН
Слайд 9Высказывание, не содержащее логические связки, называется элементарным.
ЭЛЕМЕНТАРНЫЕ высказываниЯ
Слайд 10 В алгебре высказываний над высказываниями можно производить определённые логические операции, в
результате которых получаются новые высказывания.
Отрицание
Конъюнкция
Дизъюнкция
Импликация
Эквиваленция
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Слайд 11Это высказывание, истинное тогда и только тогда, когда А – ложное,
и ложное тогда и только тогда, когда А – истинное.
Логические связки
Не А
неверно, что А
А не имеет места быть
Обозначение
Отрицание высказывания А
Слайд 12Конъюнкция двух высказываний А и В
А и В
А, а В
А,
но В
как А, так и В
не только А, но и В
А вместе с В
А, в то время как В
как А, так и В
не только А, но и В
А вместе с В
А, в то время как В
Это высказывание, истинное тогда и только тогда, когда оба высказывания А и В истинные.
конъюнкция - соединение
Логические связки
Обозначение
Слайд 13Дизъюнкция двух высказываний А и В
Это высказывание ложное тогда и только
тогда, когда ложными являются оба высказывания A и B.
А или В
или А, или В, или оба вместе
дизъюнкция - разъединение
Логические связки
Обозначение
Слайд 14Импликация двух высказываний А и В
Это высказывание ложное тогда и только
тогда, когда первое высказывание A – истинное, а второе высказывание B – ложное.
Если А, то В
А, только если В
А влечет В
из А следует В
А достаточно для В
В необходимо для А
В тогда, когда А
импликация - сплетение
(тесное связывание)
Логические связки
Обозначение
Слайд 15Эквиваленция двух высказываний А и В
Это высказывание истинное тогда и только
тогда, когда либо истинны, либо ложны оба высказывания A и В одновременно.
А тогда и только тогда, когда В;
А эквивалентно В;
А необходимо и достаточно для В.
Логические связки
Обозначение
Слайд 16Порядок выполнения
логических операций
Отрицание
Конъюнкция
Дизъюнкция
Импликация
Эквиваленция
Изменить порядок выполнения операций может расстановка скобок
Слайд 17Формализация высказываний
При формализации высказываний удобно использовать следующий алгоритм:
Выделить в данном высказывании
все логические связки.
Определить, какой логической операции соответствует каждая логическая связка, ввести обозначение операций.
Слайд 18Формализация высказываний
При формализации высказываний удобно использовать следующий алгоритм:
Выделить в данном высказывании
все элементарные высказывания и обозначить их заглавными буквами латинского алфавита (различные высказывания обозначаются разными буквами).
Представить формулу для данного составного высказывания, связывая заглавные буквы латинского алфавита символами логических операций, учитывая при этом смысл высказывания, приоритет логических операций, расставляя, в случае необходимости, скобки.
Слайд 19Формализация высказываний
С=«Положительный ряд сходится тогда и только тогда, когда множество его
частичных сумм ограничено сверху».
С=«Положительный ряд сходится тогда и только тогда, когда множество его частичных сумм ограничено сверху».
С=«Положительный ряд сходится тогда и только тогда, когда множество его частичных сумм ограничено сверху».
С=«Положительный ряд сходится тогда и только тогда, когда множество его частичных сумм ограничено сверху».
А = «Положительный ряд сходится»
В = «Множество частичных сумм положительного ряда ограничено сверху».
Слайд 20Формализация высказываний
D = «Верность теорий проверяется не опытом, а временем»
D =
«Верность теорий проверяется не опытом, а временем»
D = «Верность теорий проверяется не опытом, а временем»
D = «Верность теорий проверяется не опытом, а временем»
А = «Верность теорий проверяется опытом»
В = «Верность теорий проверяется временем»
