- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Введение в теорию вероятностей, комбинаторику и статистику
Содержание
- 1. Презентация по математике на тему Введение в теорию вероятностей, комбинаторику и статистику
- 2. Слово « статистика» происходит от латинского status
- 3. 2. Статистика – это отрасль практической деятельности, направленной на сбор, обработку, анализ статистических данных.СТАТИСТИКА
- 4. 3. Статистика –это совокупность статистических данных, характеризующих
- 5. СТАТИСТИКАСтатистическая информация о результатах наблюдений или экспериментов
- 6. ПРИМЕР 1Игральный кубик бросили 12 раз и
- 7. КОМБИНАТОРИКАКомбинаторика – это раздел математики, посвящённый задачам
- 8. ПРИМЕР 2Несколько стран в качестве символа своего
- 9. ПРИМЕР 3Сколько чётных двузначных чисел можно составить
- 10. ПРИМЕР 4На завтрак Вова может выбрать плюшку,
- 11. Теория вероятностей Теория вероятностей -есть математический анализ
- 12. Теория вероятностей Почему явления представляются нам случайными?1.
- 13. Теория вероятностей Виды событий. 1.Достоверное.2.Невозможное.3.Случайное.Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.
- 14. ЭТАП IИстория развитияПредыстория теории вероятностей. В этот
- 15. ЭТАП IIИстория развитияВозникновение теории вероятностей как науки.
- 16. ЭТАП IIIИстория развитияСледующий этап начинается с появления
- 17. ЭТАП IVИстория развитияСледующий этап развития теории вероятностей
- 18. ЭТАП VИстория развитияСовременный этап развития теории вероятностей.
- 19. Самостоятельное решение задач
- 20. Задача 1В кафе предлагают два первых блюда:
- 21. Задача 2Стадион имеет четыре входа: А, В,
- 22. Задача 3Составьте все возможные двузначные числа из
- 23. Задача 4 В шахматном турнире участвуют 9
Слово « статистика» происходит от латинского status ( состояние, положение вещей).1. Статистика – это научное направление (комплекс наук), объединяющее принципы и методы работы с числовыми данными, характеризующими массовые явления.
Слайд 2Слово « статистика» происходит от латинского status ( состояние, положение вещей).
1.
Статистика – это научное направление (комплекс наук), объединяющее принципы и методы работы с числовыми данными, характеризующими массовые явления.
Слайд 32. Статистика – это отрасль практической деятельности, направленной на сбор, обработку,
анализ статистических данных.
СТАТИСТИКА
Слайд 43. Статистика –это совокупность статистических данных, характеризующих какое–нибудь явление или процесс
(например, статистика рождаемости и смертности в России, статистика успеваемости учащихся и т.п.).
СТАТИСТИКА
Слайд 5СТАТИСТИКА
Статистическая информация о результатах наблюдений или экспериментов может быть представлена в
различных формах.
Простейшей из них является запись в порядке их появления – запись в ряд:
называемый простым статистическим рядом или выборкой.
Простейшей из них является запись в порядке их появления – запись в ряд:
называемый простым статистическим рядом или выборкой.
Слайд 6ПРИМЕР 1
Игральный кубик бросили 12 раз и записали выпавшие числа в
порядке их появления
3,4,5,6,6,6,5,1,4,6,1,4 ( n = 12 ).
Вариантами в ряду являются
Вариант имеют одинаковые значения.
Слайд 7КОМБИНАТОРИКА
Комбинаторика – это раздел математики, посвящённый задачам выбора и расположения предметов
из раздела множеств.
Типичной задачей комбинаторики является задача перечисления комбинаций, составленных из нескольких предметов.
Слайд 8ПРИМЕР 2
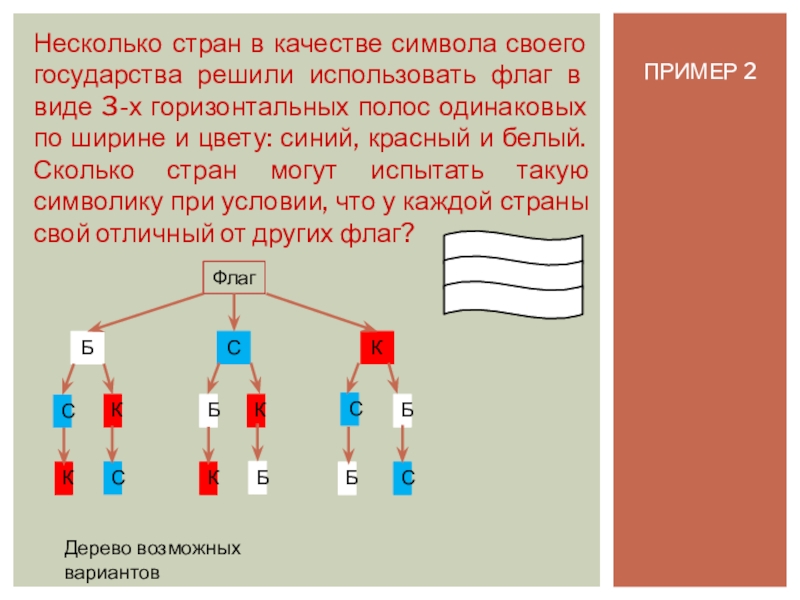
Несколько стран в качестве символа своего государства решили использовать флаг
в виде 3-х горизонтальных полос одинаковых по ширине и цвету: синий, красный и белый. Сколько стран могут испытать такую символику при условии, что у каждой страны свой отличный от других флаг?
Флаг
Б
К
С
С
К
С
К
С
С
К
К
Б
Б
Б
Б
Дерево возможных вариантов
Слайд 9ПРИМЕР 3
Сколько чётных двузначных чисел можно составить из цифр
0,1,2,4,5,9.
Составим таблицу: слева от 1–го столбца поместим первые цифры искомых чисел, сверху – вторые цифры этих чисел (чётные цифры, тогда столбцов будет три).
10
12
14
20
22
24
40
42
44
50
52
54
90
92
94
Таблица возможных вариантов
Слайд 10ПРИМЕР 4
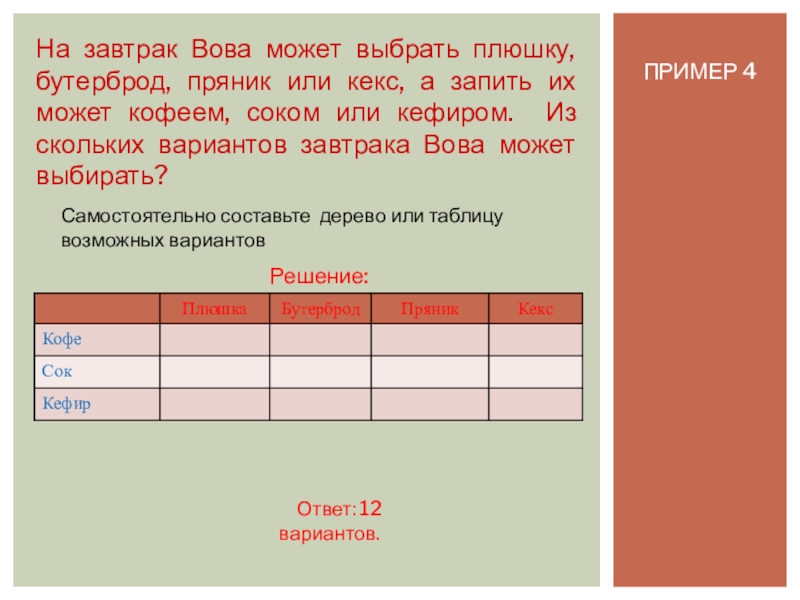
На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс,
а запить их может кофеем, соком или кефиром. Из скольких вариантов завтрака Вова может выбирать?
Самостоятельно составьте дерево или таблицу возможных вариантов
Решение:
Ответ: 12 вариантов.
Слайд 11Теория вероятностей
Теория вероятностей -
есть математический анализ понятия случайного эксперимента. Событие
и вероятность являются основными понятиями этой теории.
Слайд 12Теория вероятностей
Почему явления представляются нам случайными?
1. Отсутствие полной информации о
них.
2. Явления случайны в силу своей природы.
3. Представления о достоверности или случайности явления зависят от объективных закономерностей процесса познания.
4. Природа случайности имеет свои истоки в наших представлениях о физическом строении материи.
Слайд 13Теория вероятностей
Виды событий.
1.Достоверное.
2.Невозможное.
3.Случайное.
Предметом теории вероятностей является изучение вероятностных закономерностей
массовых однородных случайных событий.
Слайд 14ЭТАП I
История развития
Предыстория теории вероятностей. В этот период, начало которого теряется
в глубине веков, ставились и примитивно решались задачи, которые позже будут отнесены к теории вероятностей. Никаких специальных методов решения в этот период не было. Этот период закончился в XVI веке появление работ Кардано, Пачоли, Тарталья.
Слайд 15ЭТАП II
История развития
Возникновение теории вероятностей как науки.
В этот период вырабатываются
первые специфические понятия, устанавливаются первые теоремы. Начало этого периода связано с именами Паскаля, Ферма, Гюйгенса. Этот период продолжается от середины XVI века до начала XVIII века. В этот период теория вероятностей находят свои первые применения в демографии, страховом деле, оценке ошибок наблюдения.
Слайд 16ЭТАП III
История развития
Следующий этап начинается с появления работы Я. Бернулли «Искусство
предположения» (1713 год). Здесь была доказана теорема Бернулли, которая дала возможность широко применять теорию вероятностей к статистике. К этому периоду относятся работы Муавра, Лапласа, Гаусса, Пуассона, теория вероятностей начинает применяться в различных областях естествознания.
Слайд 17ЭТАП IV
История развития
Следующий этап развития теории вероятностей связан, прежде всего, с
русской (Петербургской) школой. Здесь можно назвать имена Чебышева, Маркова, Ляпунова. В это время теория вероятностей начинает широко применяться в различных областях естествознания, в первую очередь – в физике. Возникает статистическая физика, которая развивается в тесной связи с теорией вероятностей.
Слайд 18ЭТАП V
История развития
Современный этап развития теории вероятностей.
Для успешного применения теории
вероятностей к физике, биологии и другим наукам, а также к технике и военному делу необходимо было уточнить и привести в стройную систему основные понятия теории вероятностей. Поэтому этот период начался с установления аксиом науки. Первые работы этого периода связаны с именами Бернштейна, Мизеса, Бореля. Окончательное установление аксиоматики произошло в 30-е годы XX века, когда была опубликована и получила всеобщее признание аксиоматика Андрея Николаевича Колмогорова
Слайд 20Задача 1
В кафе предлагают
два первых блюда: борщ, рассольник —
и
четыре вторых блюда: гуляш, котлеты, сосиски, пельмени.
Укажите все обеды из первого и второго блюд, которые может заказать посетитель.
Проиллюстрируйте ответ, построив дерево возможных вариантов
Укажите все обеды из первого и второго блюд, которые может заказать посетитель.
Проиллюстрируйте ответ, построив дерево возможных вариантов
Слайд 21Задача 2
Стадион имеет четыре входа: А, В, С и D.
Укажите
все возможные способы, какими посетитель может войти через один вход, а выйти через другой. Сколько таких способов?
Проиллюстрируйте ответ, построив таблицу возможных вариантов.
Проиллюстрируйте ответ, построив таблицу возможных вариантов.
Слайд 22Задача 3
Составьте все возможные двузначные числа из указанных цифр, используя в
записи числа каждую из них не более одного раза: 1, 6, 8.
Проиллюстрируйте ответ, построив таблицу возможных вариантов
Проиллюстрируйте ответ, построив таблицу возможных вариантов
Слайд 23Задача 4
В шахматном турнире участвуют 9 человек. Каждый из них
сыграл с каждым по одной партии.
Сколько всего партий было сыграно?
Проиллюстрируйте ответ, построив таблицу возможных вариантов
Сколько всего партий было сыграно?
Проиллюстрируйте ответ, построив таблицу возможных вариантов
