Бектасова Гульнара Нигметовна, учитель математики
п.Основной Новоузенского района Саратовской области
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: В мире римских чисел (5 класс)
Содержание
- 1. Презентация по математике на тему: В мире римских чисел (5 класс)
- 2. Цели мероприятия: 1. Получение дополнительной информации
- 3. ПОЗНАВАТЕЛЬНАЯ ИНФОРМАЦИЯ О РИМСКИХ ЦИФРАХ
- 4. В древние времена люди пользовались для счета
- 5. Промежуточные числа образовывались путем прибавления нескольких букв
- 6. Система расположения этих
- 7. Та же логика действует и
- 8. Запрет на
- 9. ПРОИСХОЖДЕНИЕ РИМСКИХ ЦИФРНа данный момент не существует
- 10. Таким образом, цифра «I» - это не
- 11. Постепенно зарубки превратились в графические
- 12. Альтернативная теория принадлежит Альфреду Куперу, который предположил
- 13. Именно
- 14. ПРИМЕНЕНИЕ РИМСКИХ ЦИФРВ русском языке римские цифры
- 15. Номер тома в многотомной книге (иногда — номера
- 16. Иные важные события или пункты списка, например:
- 17. Валентность химических элементов.Порядковый номер ступени в звукоряде.База
- 18. МНЕМОНИЧЕСКИЕ ПРАВИЛА Соответственно M,
- 19. ЗАДАЧКИ, РЕБУСЫ, ГОЛОВОЛОМКИ Задачи со спичками. И
- 20. ЗАДАЧА С ТРЕМЯ СПИЧКАМИИтак, берем одну спичку
- 21. ГОЛОВОЛОМКА «БОКАЛ С ВИШЕНКОЙС помощью четырех спичек
- 22. ОСТАВИТЬ 1 ТРЕУГОЛЬНИКПередвиньте 1 спичку так, чтобы вместо 9 треугольников остался только один.
- 23. РАЗВЕРНУТЬ РЫБКУПереставьте три спички так, чтобы рыбка
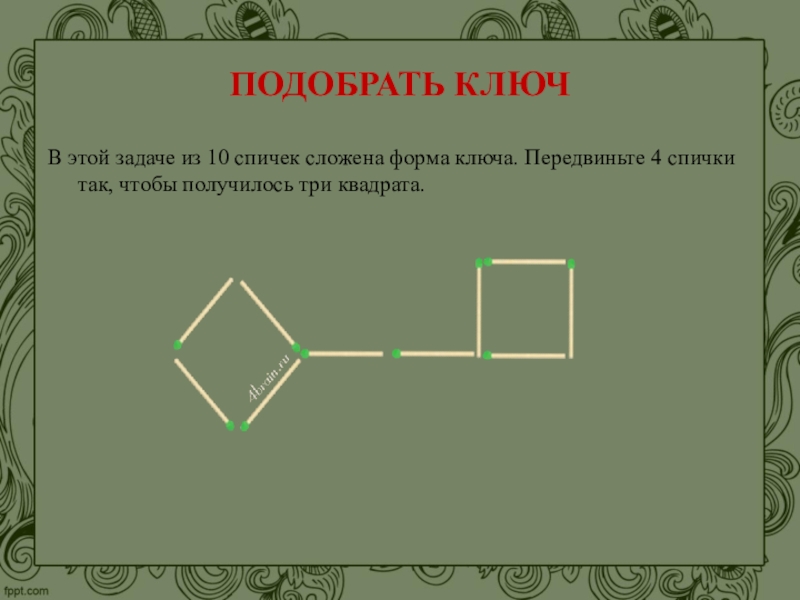
- 24. ПОДОБРАТЬ КЛЮЧВ этой задаче из 10 спичек
- 25. СЕМЬ КВАДРАТОВПереложите 2 спички так, чтобы образовать
- 26. ПОЛЕ ДЛЯ КРЕСТИКОВ - НОЛИКОВ Необходимо переложить
- 27. ЗАДАЧКИ СО СПИЧКАМИЗадача 1Перенесите одну спичку, чтобы
- 28. ЛИТЕРАТУРА1.Задачи и головоломки со спичками | Блог
Слайд 1Внеклассное мероприятие по математике для учащихся 5 классов «В МИРЕ РИМСКИХ
Слайд 2Цели мероприятия:
1. Получение дополнительной информации о римских числах;
2.развитие логического мышления;
3. раскрытие творческих способностей ребенка; 4. привитие интереса к предмету.
Слайд 4
В древние времена люди пользовались для счета пальцами, поэтому римские цифры
Слайд 5Промежуточные числа образовывались путем прибавления нескольких букв справа или слева. Сначала
Слайд 6 Система расположения этих цифр друг относительно друга такова: числа до трех
Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления – после, например:
4 = IV 6 = VI 7 = VII
Слайд 7 Та же логика действует и с другими цифрами IX =
Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.
Важно, что любая цифра не должна повторять больше трех раз, таким образом, самое длинное число до тысячи – 888.
888 = DCCCLXXXVIII
(500+100+100+100+50+10+10+10+5+1+1+1)
Слайд 8 Запрет на четвертое использование одной и той же цифры подряд стал
Также в Средневековье появилась новая римская цифра – ноль, который обозначался буквой N (от латинского nulla, ноль). 0 = N
Слайд 9ПРОИСХОЖДЕНИЕ РИМСКИХ ЦИФР
На данный момент не существует единой теории происхождения римских
Слайд 10Таким образом, цифра «I» - это не латинская или более древняя
Число 10 выглядело в этом счете следующим образом: IIIIΛIIIIX.
Именно благодаря такой записи цифр подряд мы обязаны особой системе сложения римских цифр: со временем запись числа 8 (IIIIΛIII) могла сократиться до ΛIII, что убедительно демонстрирует, каким образом римская система счета получила свою специфику.
Слайд 11 Постепенно зарубки превратились в графические символы I, V и X,
Слайд 12Альтернативная теория принадлежит Альфреду Куперу, который предположил рассмотреть римскую систему счета
Слайд 13 Именно поэтому римские цифры суммируют не только единицы, но и складывают
Слайд 14ПРИМЕНЕНИЕ РИМСКИХ ЦИФР
В русском языке римские цифры используются в следующих случаях:
Номер
Порядковый номер монарха
Номер корпуса в Вооруженных силах
ВЕК
I
Слайд 15
Номер тома в многотомной книге (иногда — номера частей книги, разделов или
В некоторых изданиях — номера листов с предисловием к книге, чтобы не исправлять ссылки внутри основного текста при изменении предисловия;
Маркировка циферблатов часов «под старину;
Слайд 16
Иные важные события или пункты списка, например:
V постулат Евклида,
II
Xx съезд КПСС,
Игры XXII Олимпиады и т. п.
Слайд 17Валентность химических элементов.
Порядковый номер ступени в звукоряде.
База гомеопатических разведений (Conium X3,
В математическом анализе римскими цифрами иногда записывается номер производной выше третьей.
Существует распространенное заблуждение о том, что современные западные размеры одежды имеют некую связь с римскими цифрами. На самом деле обозначения XXL, S, M, L и т.п. не имеют никакой связи с ними: это аббревиатуры английских слов eXtra (очень), Small (маленький), Large (большой).
Слайд 18МНЕМОНИЧЕСКИЕ ПРАВИЛА
Соответственно M, D, C, L, X,
Мы Dарим Сочные Lимоны, Хватит Vсем Iх
M – 1000, D – 500, C – 100, L – 50,
X – 10, X – 10 , V – 5, I - 1
Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам
Слайд 19ЗАДАЧКИ, РЕБУСЫ, ГОЛОВОЛОМКИ
Задачи со спичками. И не просто задачи со
Слайд 20ЗАДАЧА С ТРЕМЯ СПИЧКАМИ
Итак, берем одну спичку и видим, что с
Далее: возьмем две спички и уже, манипулируя с двумя, получаем целых четыре числа, записанных римскими цифрами:
Возьмем 3 спички. Вопрос.
Сколько чисел римских можно составить из 3 спичек?
Должно получиться 7 вариантов.
Думаем…
???
Слайд 21ГОЛОВОЛОМКА «БОКАЛ С ВИШЕНКОЙ
С помощью четырех спичек сложена форма бокала, внутри
Слайд 22ОСТАВИТЬ 1 ТРЕУГОЛЬНИК
Передвиньте 1 спичку так, чтобы вместо 9 треугольников остался
Слайд 23РАЗВЕРНУТЬ РЫБКУ
Переставьте три спички так, чтобы рыбка поплыла в обратном направлении.
Слайд 24ПОДОБРАТЬ КЛЮЧ
В этой задаче из 10 спичек сложена форма ключа. Передвиньте
Слайд 25СЕМЬ КВАДРАТОВ
Переложите 2 спички так, чтобы образовать 7 квадратов.
Соприкасающиеся друг с
Слайд 26ПОЛЕ ДЛЯ КРЕСТИКОВ - НОЛИКОВ
Необходимо переложить 3 спички так, чтобы
Нужно переместить только одну спичку в выложенном спичками арифметическом примере «8+3-4=0» так, чтобы получилось верное равенство (можно менять и знаки, цифры).
Слайд 27ЗАДАЧКИ СО СПИЧКАМИ
Задача 1
Перенесите одну спичку, чтобы данное выражение стало верным:
Задача 2
Переложите одну спичку, чтобы данное равенство стало верным: 7-5=7.
Задача 3
Переставьте одну спичку, для того чтобы равенство стало верным: 3+0=8.
Задача 4
. Переставьте 1 спичку, для того чтобы данное выражение стало верным: 4-5=1.
Задача 5
Передвиньте одну спичку, для того чтобы данное равенство стало верным: 1+8=1.
Задача 6
Передвиньте одну спичку, чтобы выражение стало верным: 5+7=7.
Слайд 28ЛИТЕРАТУРА
1.Задачи и головоломки со спичками | Блог 4brain
4brain.ru>blog/задачи-и-головоломки-со-спичками/.
2.Головоломки со спичками -
free-maht.ru>index/86-568-5-3
3.Познавательная информация о римских цифрах…
angreal.info>post346496953/