- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Тетраэдр, параллелепипед
Содержание
- 1. Презентация по математике на тему Тетраэдр, параллелепипед
- 2. AВ DАВСD – ромб, сторона которого
- 3. Многоугольник ABCDNH – фигура, составленная из отрезков.АВСDHN
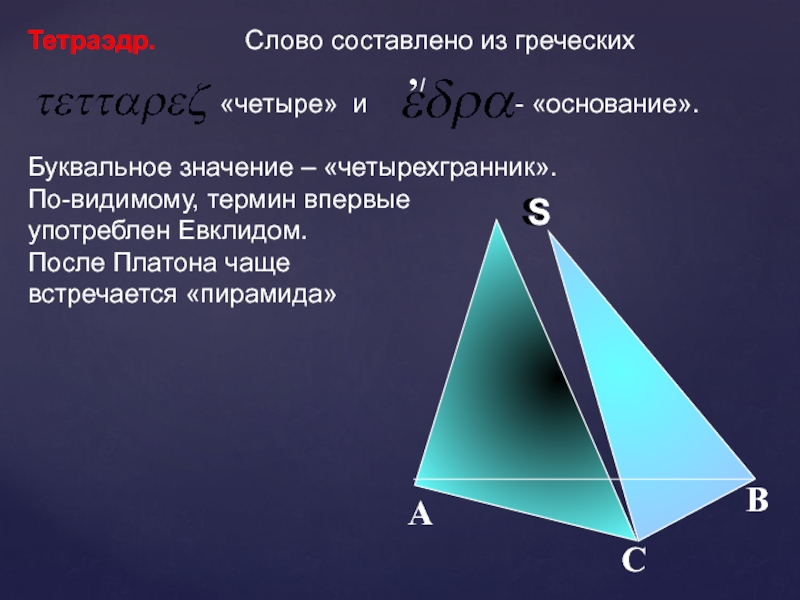
- 4. DАСВПоверхность, составленная из четырех треугольников …называется тетраэдромГрани
- 5. Слайд 5
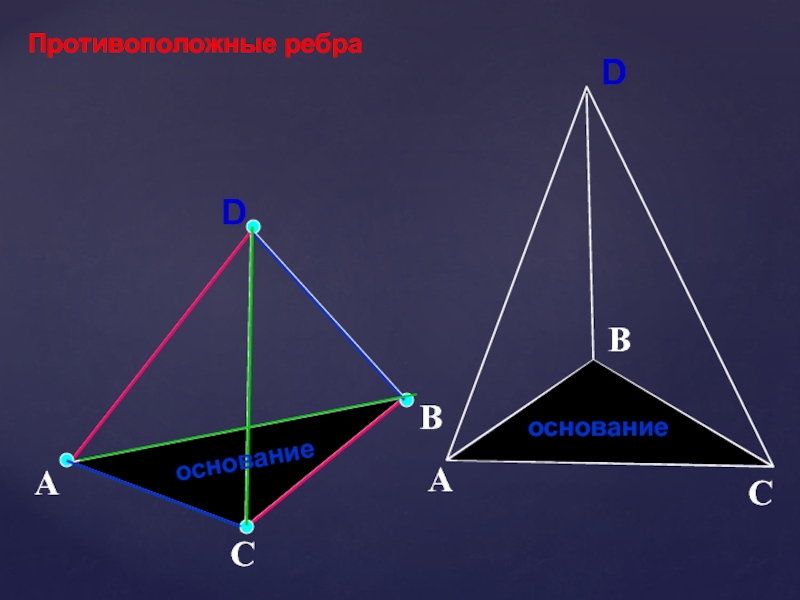
- 6. DАСВПротивоположные ребраоснованиеоснование
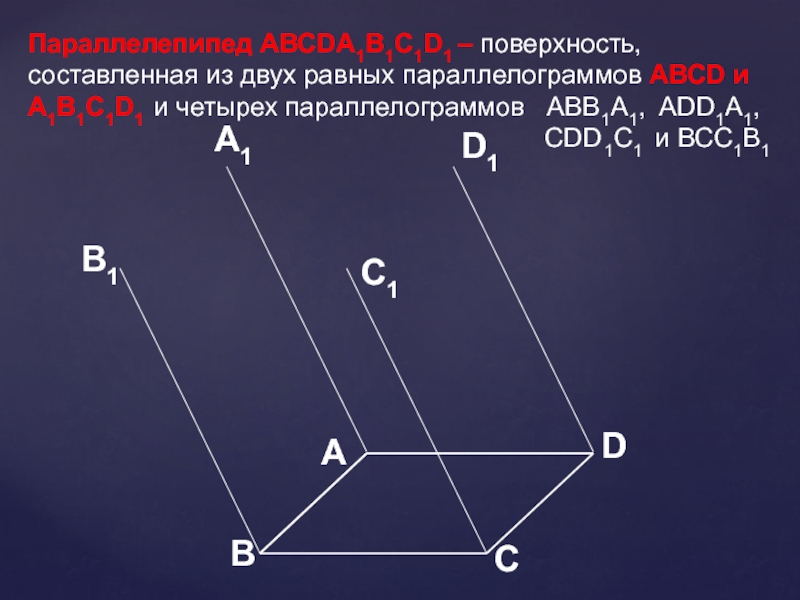
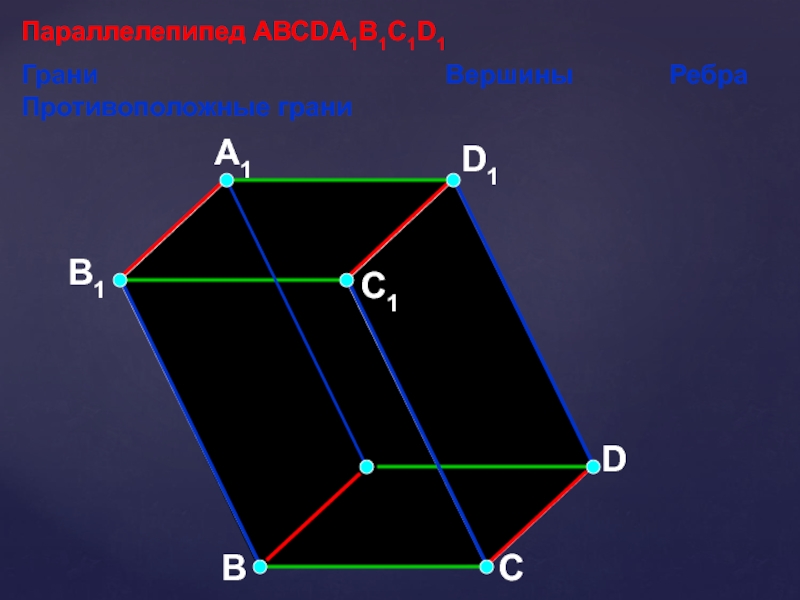
- 7. Параллелепипед АВСDA1B1C1D1 – поверхность, составленная из двух
- 8. АВСDD1С1A1B1Параллелепипед АВСDA1B1C1D1Грани
- 9. Слайд 9
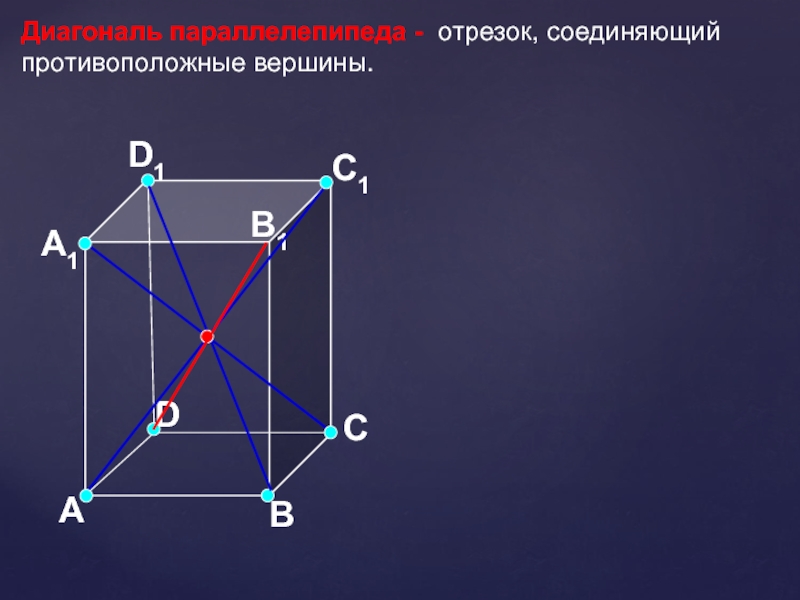
- 10. АВСDА1D1С1B1Диагональ параллелепипеда - отрезок, соединяющий противоположные вершины.
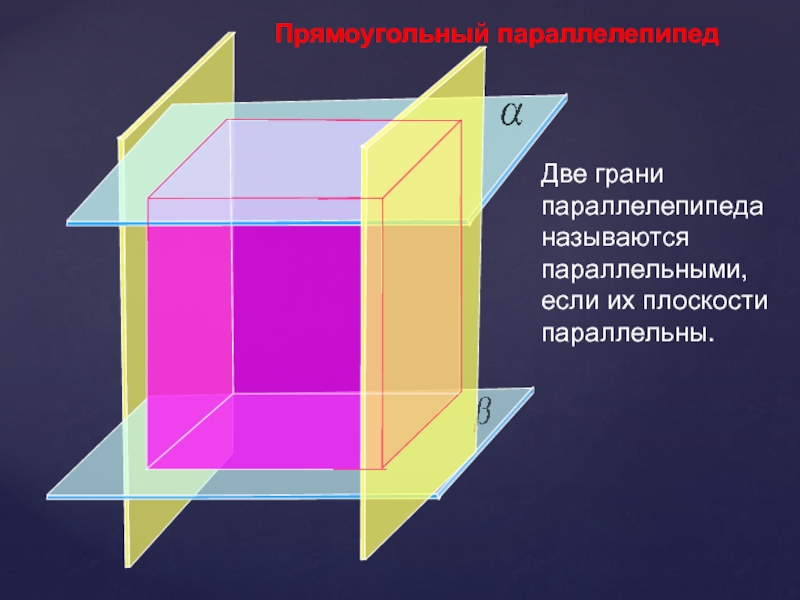
- 11. Прямоугольный параллелепипедДве грани параллелепипеда называются параллельными, если их плоскости параллельны.
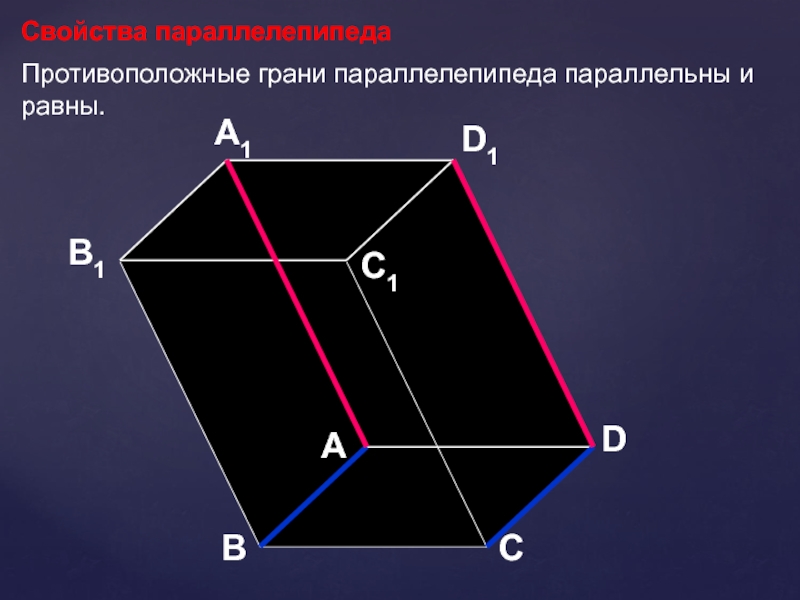
- 12. АВСDD1С1A1B1Свойства параллелепипедаПротивоположные грани параллелепипеда параллельны и равны.
- 13. АВСDD1С1A1B1Свойства параллелепипедаДиагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
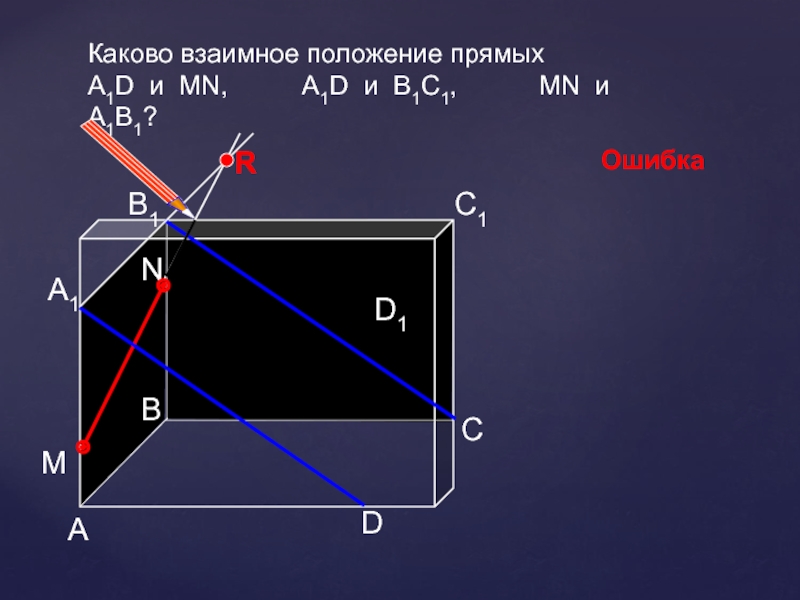
- 14. АDСВB1С1D1А1Каково взаимное положение прямых А1D и MN,
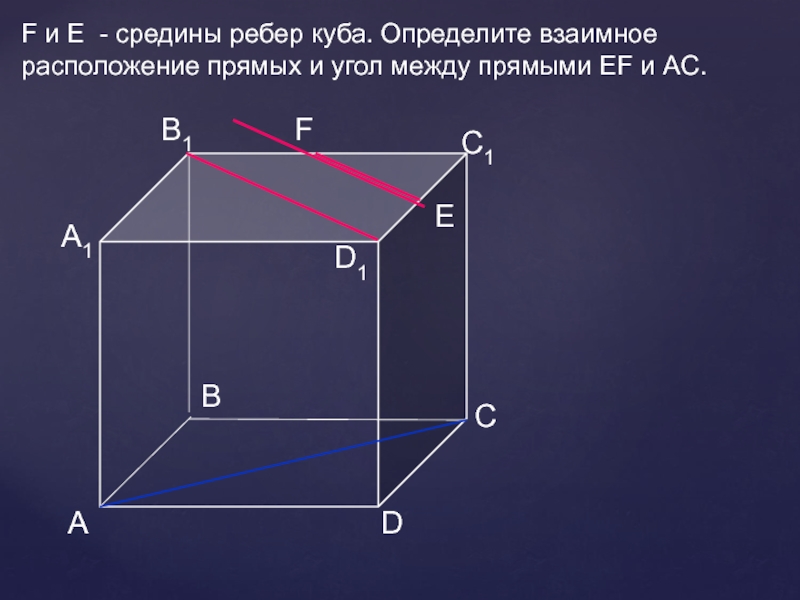
- 15. АDСВB1С1D1А1FEF и E - средины ребер куба.
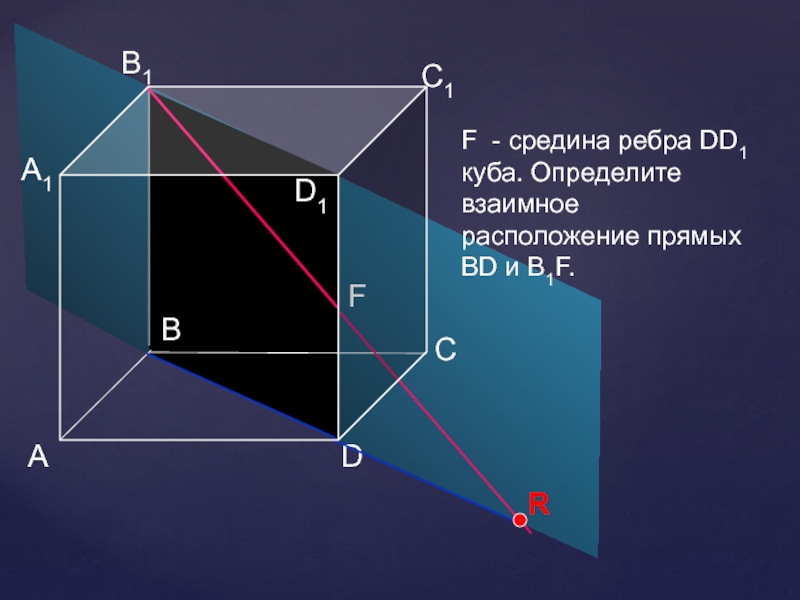
- 16. АDСВB1С1D1А1FF - средина ребра DD1 куба. Определите взаимное расположение прямых BD и B1F.
- 17. АDСВB1С1D1А1FEF и E - средины ребер куба.
- 18. АDСВB1С1D1А1FF и Е - средины ребер куба.
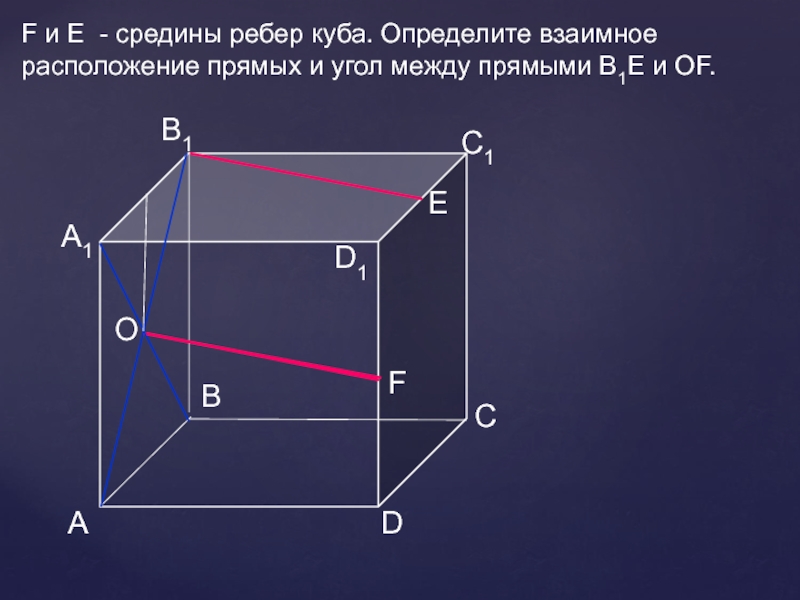
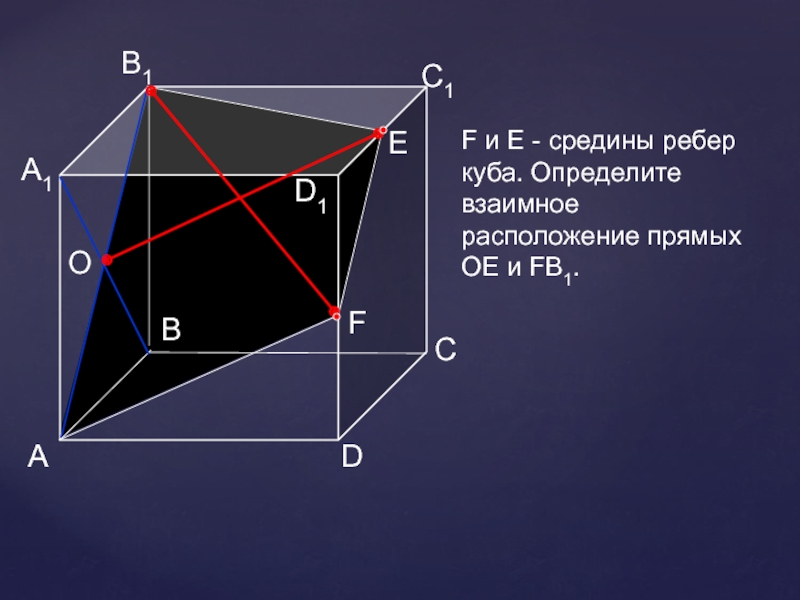
- 19. АDСВB1С1D1А1FF и Е - средины ребер куба. Определите взаимное расположение прямых ОЕ и FВ1.ЕО
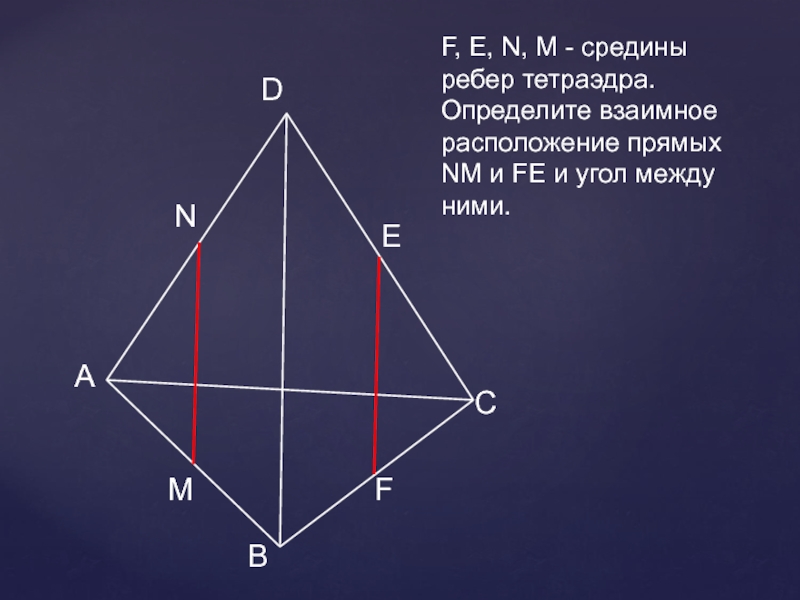
- 20. АВСDNMEFF, Е, N, M - средины ребер
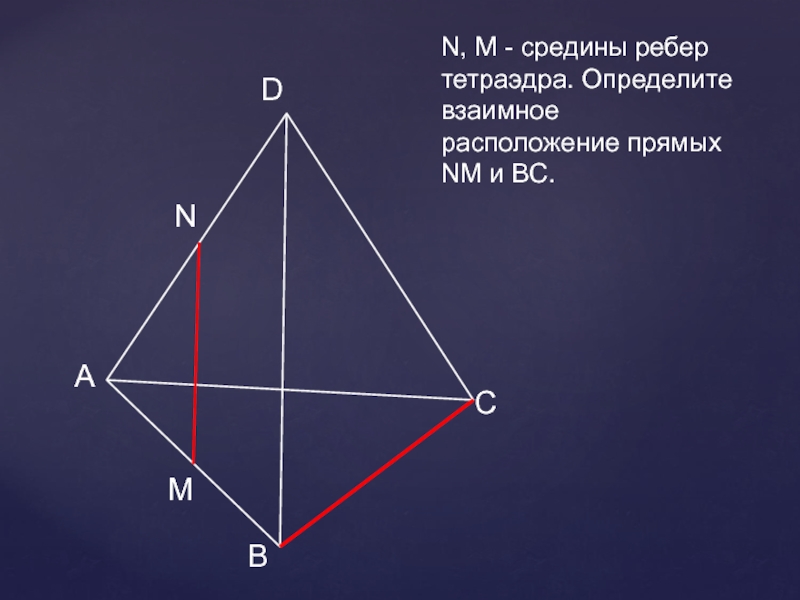
- 21. АВСDNMN, M - средины ребер тетраэдра. Определите взаимное расположение прямых NM и ВС.
- 22. АВСDNMN, M, Р и К - средины ребер тетраэдра. Определите взаимное расположение прямых NК и МС.РК
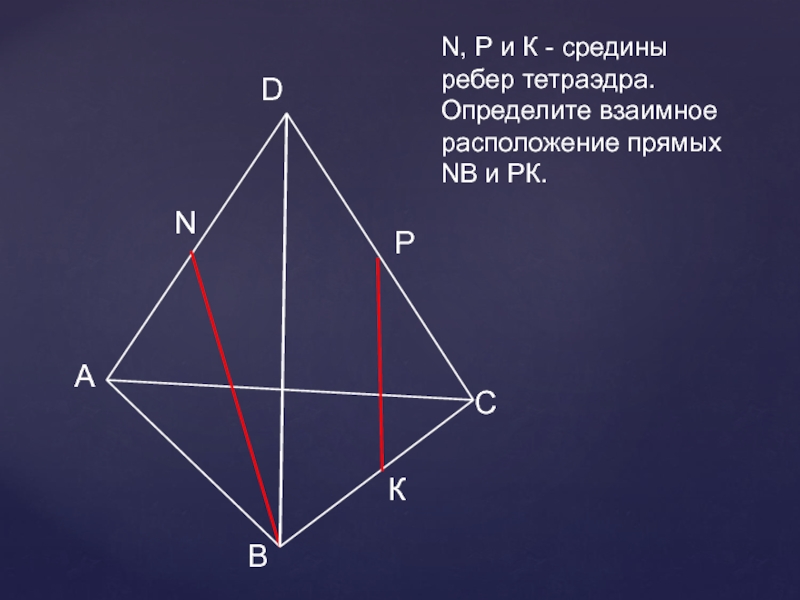
- 23. АВСDNN, Р и К - средины ребер тетраэдра. Определите взаимное расположение прямых NВ и РК.РК
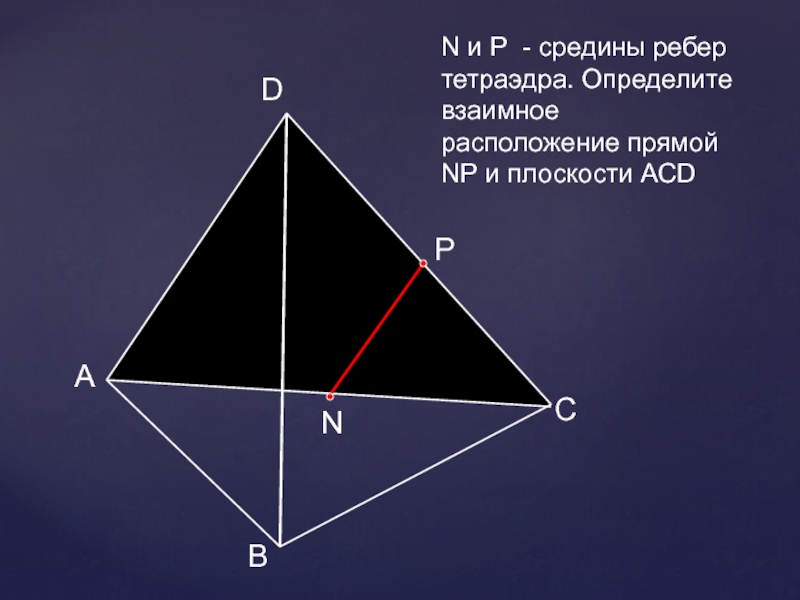
- 24. АВСDNN и Р - средины ребер тетраэдра. Определите взаимное расположение прямой NР и плоскости АСDР
- 25. АВСDОпределите взаимное расположение прямой DВ и плоскости АСD
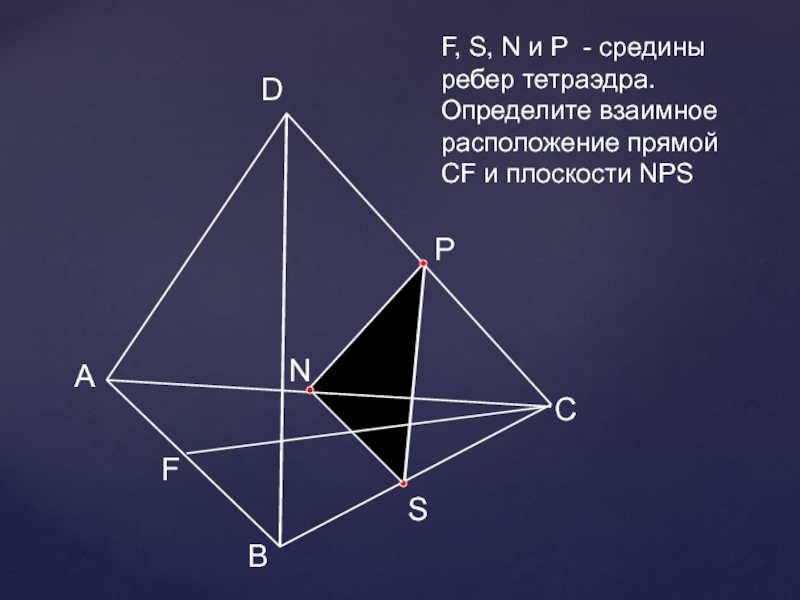
- 26. АВСDNF, S, N и Р - средины
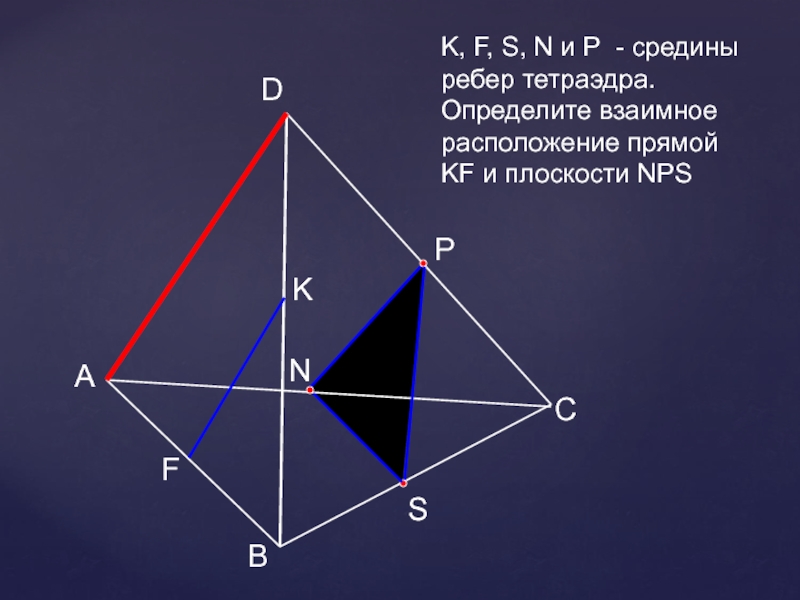
- 27. АВСDNK, F, S, N и Р -
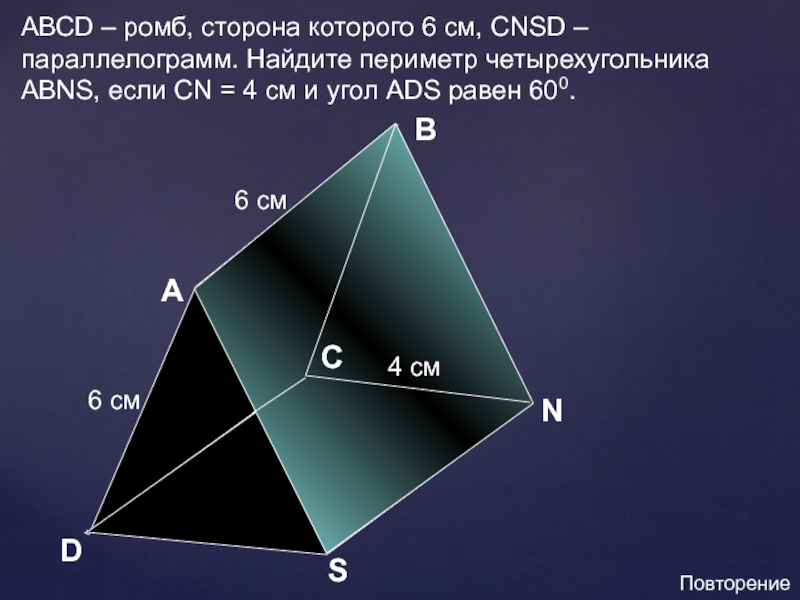
AВ DАВСD – ромб, сторона которого 6 см, СNSD – параллелограмм. Найдите периметр четырехугольника АВNS, если СN = 4 см и угол ADS равен 600.CNS6 см6 см4 смПовторение
Слайд 2
A
В
D
АВСD – ромб, сторона которого 6 см, СNSD –
параллелограмм. Найдите периметр четырехугольника АВNS, если СN = 4 см и угол ADS равен 600.
C
N
S
6 см
6 см
4 см
Повторение
Слайд 4
D
А
С
В
Поверхность, составленная из четырех треугольников …
называется тетраэдром
Грани
Вершины Ребра
Слайд 7Параллелепипед АВСDA1B1C1D1 – поверхность, составленная из двух равных параллелограммов АВСD и
A1B1C1D1 и четырех параллелограммов АВВ1А1, ADD1A1,
CDD1C1 и ВСС1В1
CDD1C1 и ВСС1В1
А
В
С
D
Слайд 11
Прямоугольный параллелепипед
Две грани параллелепипеда называются параллельными, если их плоскости параллельны.
Слайд 12
А
В
С
D
D1
С1
A1
B1
Свойства параллелепипеда
Противоположные грани параллелепипеда параллельны и равны.
Слайд 13
А
В
С
D
D1
С1
A1
B1
Свойства параллелепипеда
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой
пополам.
Слайд 15
А
D
С
В
B1
С1
D1
А1
F
E
F и E - средины ребер куба. Определите взаимное
расположение прямых
и угол между прямыми EF и AC.
Слайд 17
А
D
С
В
B1
С1
D1
А1
F
E
F и E - средины ребер куба. Определите взаимное
расположение прямых
и угол между прямыми В1Е и ОF.
О
Слайд 18
А
D
С
В
B1
С1
D1
А1
F
F и Е - средины ребер куба. Определите взаимное
расположение прямых
АС и FЕ и угол между ними.
Е
Слайд 19
А
D
С
В
B1
С1
D1
А1
F
F и Е - средины ребер куба. Определите взаимное
расположение прямых
ОЕ и FВ1.
Е
О
Слайд 20
А
В
С
D
N
M
E
F
F, Е, N, M - средины ребер тетраэдра. Определите взаимное
расположение
прямых NM и FЕ и угол между ними.
Слайд 22
А
В
С
D
N
M
N, M, Р и К - средины ребер тетраэдра. Определите взаимное
расположение прямых NК и МС.
Р
К
Слайд 24
А
В
С
D
N
N и Р - средины ребер тетраэдра. Определите взаимное
расположение прямой
NР и плоскости АСD
Р
Слайд 26
А
В
С
D
N
F, S, N и Р - средины ребер тетраэдра. Определите взаимное
расположение прямой CF и плоскости NPS
Р
S
F
Слайд 27
А
В
С
D
N
K, F, S, N и Р - средины ребер тетраэдра. Определите
взаимное
расположение прямой KF и плоскости NPS
расположение прямой KF и плоскости NPS
Р
S
F
K