ль в порядке-
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Пожелаю всем удачи.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Сравнение десятичных дробей 6 класс
Содержание
- 1. Презентация по математике на тему Сравнение десятичных дробей 6 класс
- 2. Сравнение десятичных дробей.
- 3. Цель урока:Познакомить учащихся с алгоритмом сравнения десятичных
- 4. «Расскажи мне, и я забуду, Покажи
- 5. Прочитайте числа:2,5 0,12 7,03
- 6. Сравните:569 и 98 367 и
- 7. Проверь себя569 > 98 367
- 8. Так как 3/10 = 30/100
- 9. Вывод1.Если к десятичной дроби приписать справа какое
- 10. Напишите десятичную дробьа) с четырьмя знаками после
- 11. Проверь себяа) 0,87 = 0,8700
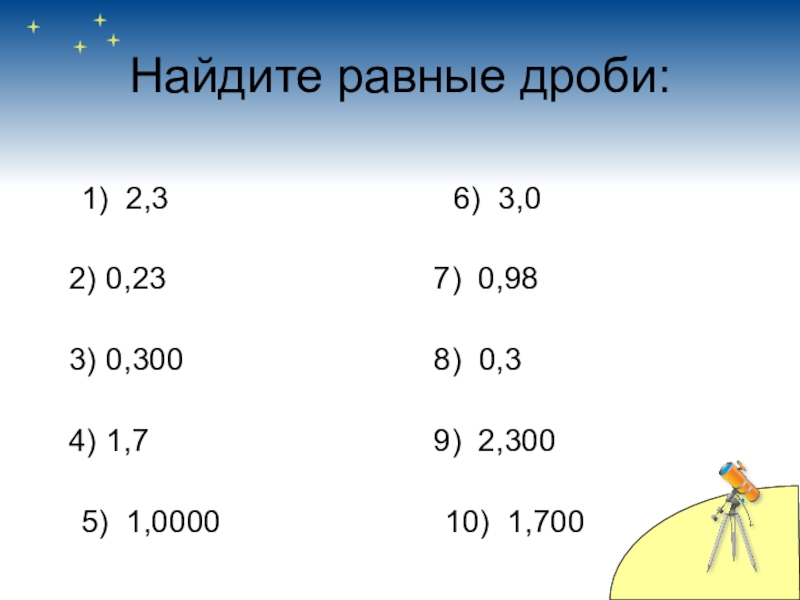
- 12. Найдите равные дроби:1) 2,3
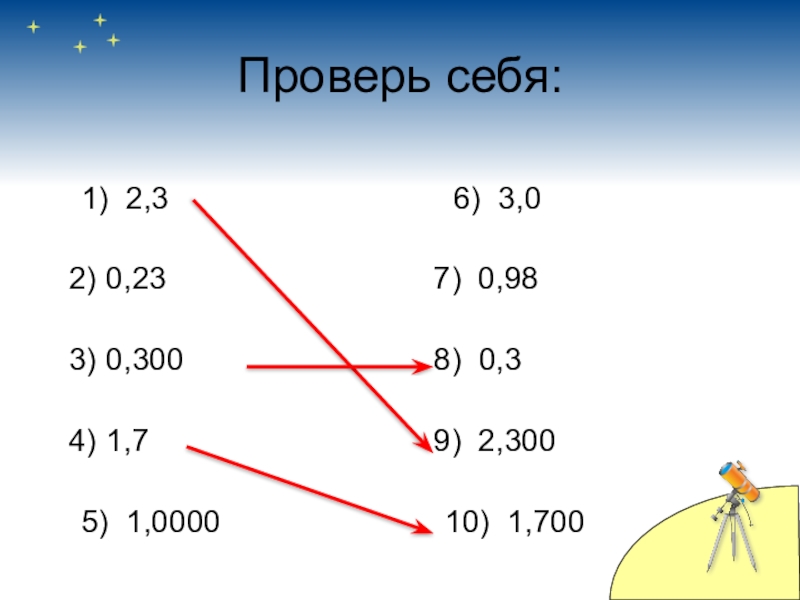
- 13. Проверь себя:1) 2,3
- 14. Десятичные дроби, как и натуральные числа, сравниваем
- 15. Сравним дроби: 3,12 и 5,4Сравниваем целые части
- 16. Сравним дроби: 2,67 и 2,8Сравниваем целые части
- 17. Сравним дроби: 1,8 и 1,82Уравняем число разрядов,
- 18. Алгоритм сравнения десятичных дробей Десятичные дроби,
- 19. Сравните числа 85,09 и 67,99
- 20. Проверь себя 85,09 > 67,99
- 21. Расположите числа в порядке убывания а) 7,34; 7,4; 7,3б) 2,356; 2,35; 2,36
- 22. Проверь себя а) 7,4; 7,34; 7,3б) 2,36; 2,356; 2,35
- 23. Замените значок « ⃰ » цифрой
- 24. Проверь себя:
- 25. Самостоятельная работа Из
- 26. Проверь себя
- 27. Итог урока. Что нового узнали? Чему
- 28. Возьмите листочки и укажите степень вашего усвоения
- 29. Молодцы !
Сравнение десятичных дробей.
Слайд 3Цель урока:
Познакомить учащихся с алгоритмом сравнения десятичных дробей;
формировать умения учащихся пользоваться
алгоритмом сравнения десятичных дробей;
развивать умения располагать дроби
в порядке возрастания и убывания.
развивать умения располагать дроби
в порядке возрастания и убывания.
Слайд 4
«Расскажи мне, и я забуду,
Покажи мне, и я запомню,
Дай мне попробовать,
и я научусь».
(Древняя китайская пословица)
и я научусь».
(Древняя китайская пословица)
Слайд 9Вывод
1.Если к десятичной дроби приписать справа какое угодно число нулей, то
получится дробь, равная данной.
0,7 = 0,70 = 0,700;
141 = 141,0 = 141,00 = 141,000
2.Если в десятичной дроби последние цифры – нули, то, отбросив их, получим дробь, равную данной.
26,100 = 26,10 = 26,1.
Слайд 10Напишите десятичную дробь
а) с четырьмя знаками после запятой, равную 0,87
б) с
тремя знаками после запятой, равную 35
в) с двумя знаками после запятой, равную 8,40000
в) с двумя знаками после запятой, равную 8,40000
Слайд 14Десятичные дроби, как и натуральные числа, сравниваем по разрядам. Если целые части
десятичных дробей различны, то больше та дробь, у которой больше целая часть.
Если целые части десятичных дробей одинаковы, то больше та дробь, у которой больше первый из несовпавших разрядов после запятой.
Алгоритм сравнения десятичных дробей
Слайд 16Сравним дроби: 2,67 и 2,8
Сравниваем целые части 2 и 2:
2 = 2
сравниваем десятые 6 и 8: 6 < 8
значит 2,67 < 2,8
сравниваем десятые 6 и 8: 6 < 8
значит 2,67 < 2,8
Слайд 17Сравним дроби: 1,8 и 1,82
Уравняем число разрядов, приписав к первой дроби
цифру 0 : 1,80 и 1,82
Сравниваем целые части 1 и 1: 1 = 1
сравниваем десятые 8 и 8: 8 = 8
сравниваем сотые 0 и 2: 0 < 2
значит 1,8 < 1,82
Сравниваем целые части 1 и 1: 1 = 1
сравниваем десятые 8 и 8: 8 = 8
сравниваем сотые 0 и 2: 0 < 2
значит 1,8 < 1,82
Слайд 18Алгоритм сравнения десятичных дробей
Десятичные дроби, как и натуральные числа, сравниваем
по разрядам.
Если целые части десятичных дробей различны, то больше та дробь, у которой больше целая часть.
Если целые части десятичных дробей одинаковы, то больше та дробь, у которой больше первый из несовпавших разрядов после запятой.
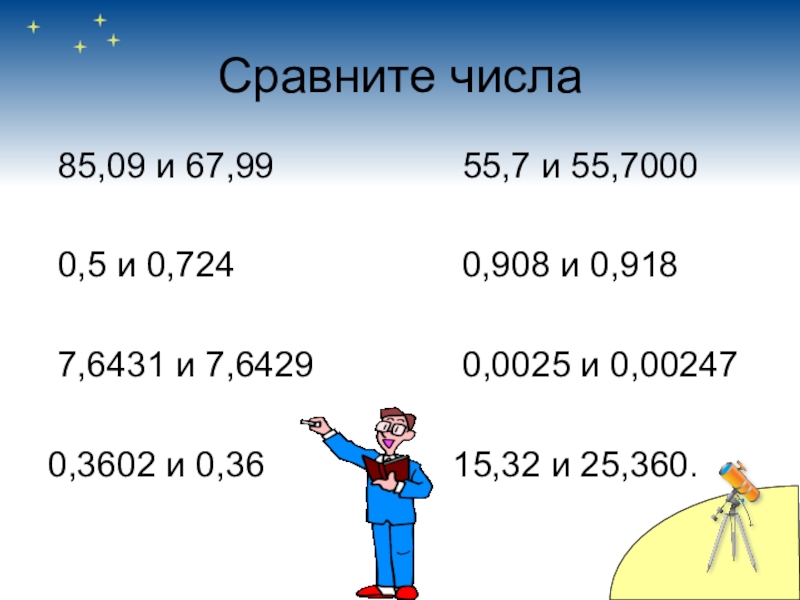
Слайд 19Сравните числа
85,09 и 67,99
55,7 и 55,7000
0,5 и 0,724 0,908 и 0,918
7,6431 и 7,6429 0,0025 и 0,00247
0,3602 и 0,36 15,32 и 25,360.
0,5 и 0,724 0,908 и 0,918
7,6431 и 7,6429 0,0025 и 0,00247
0,3602 и 0,36 15,32 и 25,360.
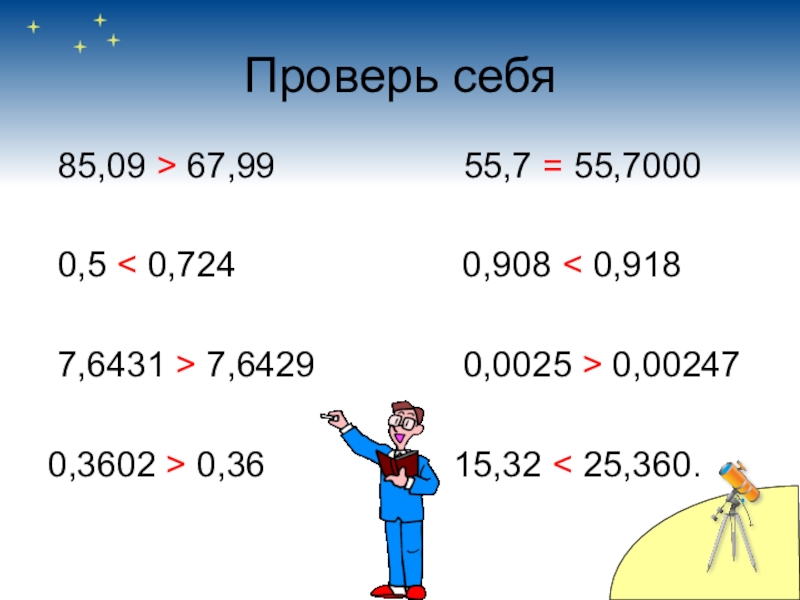
Слайд 20Проверь себя
85,09 > 67,99
55,7 = 55,7000
0,5 < 0,724 0,908 < 0,918
7,6431 > 7,6429 0,0025 > 0,00247
0,3602 > 0,36 15,32 < 25,360.
0,5 < 0,724 0,908 < 0,918
7,6431 > 7,6429 0,0025 > 0,00247
0,3602 > 0,36 15,32 < 25,360.
Слайд 23 Замените значок « ⃰ » цифрой так, чтобы полученная запись
была верной:
1) 5,688 < 5,6*1;
2) 71,09* < 71,091;
3) 9,*57 > 9,499;
Слайд 25 Самостоятельная работа
Из верных равенств составьте слово:
М)14,2
14,20
С) 8,7 > 8,608
Р)8,547 > 8,474
А) 14,13 > 12,13
В)72,03 < 72,18
Н) 37,24 < 38,24
С) 8,7 > 8,608
Р)8,547 > 8,474
А) 14,13 > 12,13
В)72,03 < 72,18
Н) 37,24 < 38,24
О)10,72 < 10,69
Е) 0,095 < 0,1
Н) 3,7 > 3,666
И) 0,37 > 0,368
К) 1,3 < 1,237
Е) 5,603 > 5,6
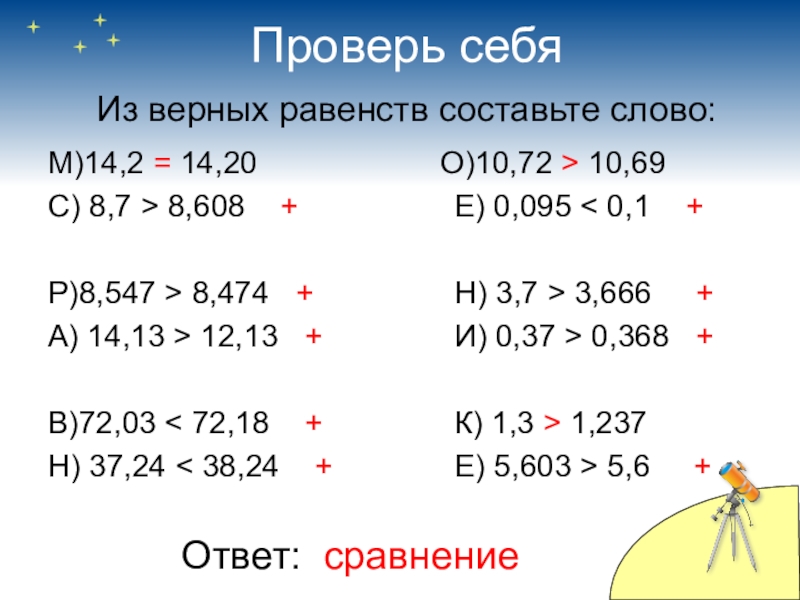
Слайд 26 Проверь себя
Из верных равенств составьте слово:
М)14,2
= 14,20
С) 8,7 > 8,608 +
Р)8,547 > 8,474 +
А) 14,13 > 12,13 +
В)72,03 < 72,18 +
Н) 37,24 < 38,24 +
С) 8,7 > 8,608 +
Р)8,547 > 8,474 +
А) 14,13 > 12,13 +
В)72,03 < 72,18 +
Н) 37,24 < 38,24 +
О)10,72 > 10,69
Е) 0,095 < 0,1 +
Н) 3,7 > 3,666 +
И) 0,37 > 0,368 +
К) 1,3 > 1,237
Е) 5,603 > 5,6 +
Ответ: сравнение
Слайд 27
Итог урока.
Что нового узнали?
Чему научились?
Трудно? Легко?
Как бы вы оценили
свою работу на уроке?
Слайд 28Возьмите листочки и укажите степень вашего усвоения материала:
усвоен полностью, могу выполнять;
усвоен
полностью, но затрудняюсь в применении;
усвоен частично;
не усвоен.
усвоен частично;
не усвоен.
